轮廓检测

yange大约 17 分钟数字图像处理数字图像处理

1. 轮廓检测

前言

定义

轮廓可简单理解为由连续边界点连接而成的曲线，这些点具有相同或相近的颜色/灰度，是图像目标的外部特征，对图像分析、目标识别及理解等深层处理意义重大。

轮廓提取基本原理
针对背景黑、目标白的二值图像，提取逻辑为：若找到某白色点且其8邻域（或4邻域）均为白色，则该点为目标内部点，需置为黑色（视觉上相当于“掏空”内部）；否则保持白色——此类白色点即为目标的轮廓点。通常，寻找轮廓前需通过阈值化或Canny边缘检测将图像转为二值图。

边缘提取与轮廓检测的区别 👇

边缘提取：聚焦图像中像素点的明暗突变（梯度变化大的位置），偏向底层像素级变化。例如Canny边缘检测，结果保存为与源图同尺寸、同类型的“边缘图”（仅标记边缘位置）。
轮廓检测：聚焦对象的语义边界，偏向高层目标级特征。例如OpenCV的findContours()函数，会输出每个轮廓的点向量（记录边界坐标），还会提供图像的拓扑信息（如某轮廓的前/后一个轮廓索引）。

查找轮廓Api：

cv2.findContours(image, mode, method[, contours[, hierarchy[, offset]]]) 
参数说明：

- image：输入图像，单通道，8位或32位。
- mode：轮廓检索模式，决定了轮廓的层次结构。 四种方式：cv2.RETR_EXTERNAL（只检索最外面的轮廓）、cv2.RETR_LIST（检索所有的轮廓，但不建立轮廓之间的层次结构）、cv2.RETR_CCOMP（检索所有的轮廓，并将它们组织成两级层次结构。顶层是外部边界，第二层是内部边界）、cv2.RETR_TREE（检索所有的轮廓，并将它们组织成嵌套的层次结构）。

- method：轮廓近似方法，决定了如何对轮廓进行近似。有两种方式：cv2.CHAIN_APPROX_NONE：存储所有的轮廓点，相邻的两个点的像素位置差不超过1。
cv2.CHAIN_APPROX_SIMPLE：压缩⽔平⽅向，垂直⽅向，对⻆线⽅向的元素，只保留该⽅向的终点坐标，例如⼀个矩形轮廓只需4个点来保存轮廓信。如下图5所示

返回值：

- image：输入图像的副本，轮廓被绘制在该图像上。
- contours：轮廓的列表，每个轮廓都是一个Numpy数组，表示轮廓的边界点。

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt

# 1 图像读取
img = cv.imread('./img/hunan.png')

imgray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

# 2 边缘检测
canny = cv.Canny(imgray, 127, 255, 0)

# 3 轮廓提取
contours, hierarchy = cv.findContours(canny, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)

# 4 找到面积最大的前10个轮廓
if len(contours) > 0:
    # 计算每个轮廓的面积，并保留索引信息
    areas_with_index = [(cv.contourArea(contour), idx) for idx, contour in enumerate(contours)]
    
    # 按面积降序排序
    areas_with_index.sort(reverse=True, key=lambda x: x[0])
    
    # 获取前4大的轮廓索引
    top_10_indices = [idx for area, idx in areas_with_index[:4]]
    top_10_areas = [area for area, idx in areas_with_index[:4]]
    
    print(f"找到 {len(contours)} 个轮廓")
    
    # 方法：用同一种颜色绘制所有轮廓
    result_img2 = img.copy()
    for contour_idx in top_10_indices:
        img_with_contours_same_color = cv.drawContours(result_img2, contours, contour_idx, (0, 0, 255), 2)

    
else:
    print("未找到任何轮廓")


# 5 图像显示
plt.figure(figsize=(20, 10))

plt.subplot(231), plt.imshow(cv.cvtColor(img, cv.COLOR_BGR2RGB))
plt.title('原始图像'), plt.axis('off')

plt.subplot(232), plt.imshow(canny, cmap='gray')
plt.title('Canny边缘检测'), plt.axis('off')

plt.subplot(234), plt.imshow(cv.cvtColor(img_with_contours_same_color, cv.COLOR_BGR2RGB))
plt.title('前10大轮廓（同色）'), plt.axis('off')


plt.tight_layout()
plt.show()

2. 不变矩

前言

定义

2. 不变矩：几何特征的升级版

几何特征虽然直观，但有一个明显缺点：对变换敏感。比如你拍一张正方形的照片，如果手机倾斜拍摄（旋转）、站远一点（缩小）或移动位置（平移），它的“面积”“周长”数值可能不变，但“质心位置”“方向”会变——如果直接用原始几何特征（比如“边界的方向”），不同拍摄条件下的同一个正方形会被误判成不同形状。

矩：是概率论和统计学中用来描述数据分布特征的量，它反映了数据在各个位置上的加权平均。矩可以用来描述数据的集中趋势、离散程度、对称性等特性。矩的作用：用数学数字概括物体的形状。

但现实中，我们看物体常会「变角度」：

猫可能站着、躺着、侧身（旋转）；
拍照时手抖歪了（倾斜）；
离得近拍显大，离得远拍显小（缩放）；
甚至镜子里的倒影（镜像）。

普通的「矩」 会跟着这些变化变：比如猫躺下了，重心位置变了，普通矩的值也会变，那我们用这组数字去识别猫时，就会认不出来。

不变矩就是为了解决这个问题诞生的：它是一组特殊的几何特征，无论形状如何平移、旋转或缩放，这些特征的数值都保持不变。就像给形状办了一张“身份证”，无论它怎么动、怎么变，身份证上的关键信息（如指纹）始终一致。

常用的不变矩是 7个，这里不列举数学公式（要看公式，教材的186页),但可以粗糙理解为它们分别对应：

描述“整体大小 ”的归一化特征；
描述“x/y方向胖瘦比例 ”的特征；
描述“倾斜程度 ”的特征；
描述“x方向对称性 ”的特征；
描述“y方向对称性 ”的特征；
描述“综合倾斜+对称性 ”的特征；
描述“高阶细节（如凹凸）”的特征。

例题9-1 对图像进行各种几何变换，观察不变矩的变化情况。 👇 👇

图像经过旋转、缩放、平移后的效果如图9-7所示。调用 moment_invariants()子函数可以求得图像的7个不变矩，在子函数中为了减小动态范围，将计算得到的不变矩取对数。各图像的不变矩如上表所示，可见图像经过各种几何变换后所求得的不变矩具有较好的一致性。

代码如下：

import numpy as np
import cv2
from matplotlib import pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

def moment_invariants(img):
    """计算图像的Hu不变矩"""
    # 确保图像是2D的灰度图像
    if len(img.shape) == 3:
        img = img[:, :, 0]  # 取第一个通道
    elif len(img.shape) > 2:
        img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    
    # 确保图像是8位单通道
    if img.dtype != np.uint8:
        img = img.astype(np.uint8)
    
    # 计算空间矩、中心矩和归一化中心矩
    moments = cv2.moments(img)
    
    # 计算Hu不变矩
    hu_moments = cv2.HuMoments(moments)
    
    # 为了避免数值过小，通常取对数
    hu_moments = -np.sign(hu_moments) * np.log10(np.abs(hu_moments) + 1e-10)
    
    return hu_moments.flatten()

# 读取图像并确保是2D灰度图
img0 = cv2.imread(r'./img/lotus.jpg', 0)
if img0 is None:
    # 如果找不到图像，创建测试图像
    img0 = np.random.randint(0, 255, (300, 300), dtype=np.uint8)
    print("使用随机生成的测试图像")

# 确保img0是2D数组
if len(img0.shape) == 3:
    img0 = img0[:, :, 0]
elif len(img0.shape) > 2:
    img0 = cv2.cvtColor(img0, cv2.COLOR_BGR2GRAY)

img = img0.copy()
textLists = []  # 用来存放几何变换名称
imgLists = []   # 用来存放几何变换图像
textLists.append("original")
imgLists.append(img.copy())

# 旋转45度
rotate_45_matrix = cv2.getRotationMatrix2D((img.shape[1] // 2, img.shape[0] // 2), -45, 1)
rotate_45_image = cv2.warpAffine(img, rotate_45_matrix, dsize=(img.shape[1], img.shape[0]))
textLists.append("rotate-45")
imgLists.append(rotate_45_image)

# 平移
img = img0.copy()
M = np.float32([[1, 0, 50], [0, 1, 50]])
translation_img = cv2.warpAffine(img, M, dsize=(img.shape[1], img.shape[0]))
textLists.append("translation")
imgLists.append(translation_img)

# 顺时针旋转90
img = img0.copy()
rotate_90_image = cv2.rotate(img, rotateCode=cv2.ROTATE_90_CLOCKWISE)  # 修复拼写错误
textLists.append("rotate-90")
imgLists.append(rotate_90_image)

# 顺时针旋转180
img = img0.copy()
rotate_180_image = cv2.rotate(img, cv2.ROTATE_180)  # 修复拼写错误
textLists.append("rotate-180")
imgLists.append(rotate_180_image)

# 缩小一半 - 修复维度问题
img = img0.copy()
half_height = img.shape[0] // 2
half_width = img.shape[1] // 2
resize_0_5_img = cv2.resize(img, (half_width, half_height))  # 直接调整大小，不需要创建零矩阵
textLists.append("shrink")
imgLists.append(resize_0_5_img)

# 逆时针旋转90
img = img0.copy()
rotate_270_image = cv2.rotate(img, rotateCode=cv2.ROTATE_90_COUNTERCLOCKWISE)
textLists.append("rotate-270")
imgLists.append(rotate_270_image)

# 计算所有图像的Hu矩
huMomentLists = []
for img in imgLists:
    # 确保传递给moment_invariants的是2D图像
    if len(img.shape) == 3:
        img_2d = img[:, :, 0]
    else:
        img_2d = img
    hu = moment_invariants(img_2d)
    huMomentLists.append(np.array(hu))
    
# 打印Hu矩结果
for descipStr, hu in zip(textLists, huMomentLists):
    descipStr += "\t"
    for mm in hu:
        descipStr += "%0.2f" % mm + '\t'
    print(descipStr)

# 显示图像 - 修复显示的图像变量
plt.figure(figsize=(15, 8))

plt.subplot(241)
plt.imshow(img0, cmap="gray")
plt.title("原图像")
plt.axis("off")

plt.subplot(242)
plt.imshow(rotate_45_image, cmap="gray")
plt.title("旋转45度")
plt.axis("off")

plt.subplot(243)
plt.imshow(rotate_90_image, cmap="gray")  # 使用正确的变量名
plt.title("顺时针旋转90")
plt.axis("off")

plt.subplot(244)
plt.imshow(rotate_180_image, cmap="gray")  # 使用正确的变量名
plt.title("顺时针旋转180")
plt.axis("off")

plt.subplot(245)
plt.imshow(rotate_270_image, cmap="gray")
plt.title("逆时针旋转90")
plt.axis("off")

plt.subplot(246)
plt.imshow(resize_0_5_img, cmap="gray")  # 直接使用resize_0_5_img，不需要额外的零矩阵
plt.title("缩小一半")
plt.axis("off")

plt.subplot(247)
plt.imshow(translation_img, cmap="gray")
plt.title("平移")
plt.axis("off")

plt.tight_layout()
plt.show()

3. 图像分割

3.1 基本全局阈值法和Otsu阈值法

前言

定义

1.基本全局阈值法

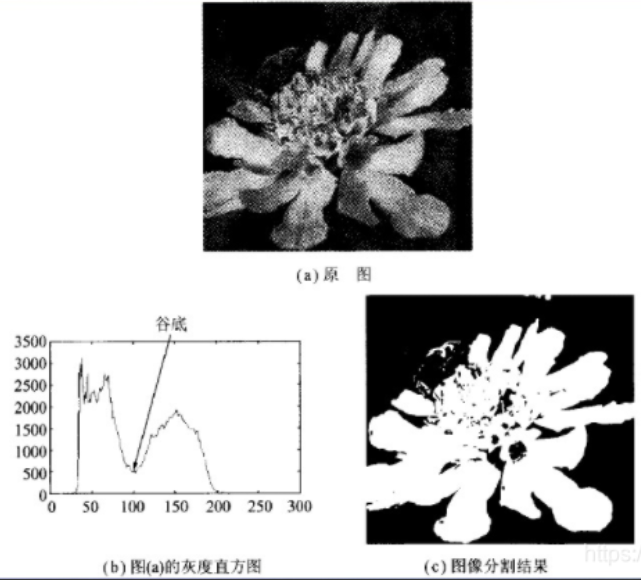
在图像分割任务中，若图像的目标（前景）和背景的灰度 差异明显（例如文档中的黑白文字、显微镜下的细胞与背景），可以通过设定一个全局统一的阈值，将所有像素分为两类：

像素灰度值 ≥ 阈值 → 归为前景（或背景）；
像素灰度值＜阈值 → 归为背景（或前景）。

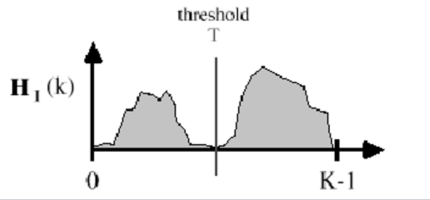
基本全局阈值法（Basic Global Thresholding）是这类方法中最基础的算法，它通过迭代优化的方式，从图像整体出发自动确定一个“最佳” 的全局阈值，从而实现简单高效的分割。

核心逻辑

基本全局阈值法的核心逻辑是：先猜测一个初始阈值，用它分割图像并计算两类像素的平均灰度，再根据两类平均灰度更新阈值，不断迭代直到阈值稳定。最终得到的阈值能较好地区分前景和背景。

2.Otsu阈值法

基本全局阈值法的核心是：先猜一个初始阈值，然后通过迭代计算两类像素的平均灰度，不断调整阈值直到稳定。这种方法虽然简单，但依赖初始值，且对前景和背景灰度分布重叠严重的图像（比如直方图没有明显双峰）效果可能不佳——因为迭代过程只是机械地平衡两类均值，未必能找到真正让两类区分最明显的阈值。

那么，有没有一种方法能直接自动找到最优阈值，而且更科学地衡量“两类区分是否明显”呢？

答案就是本节要介绍的 Otsu阈值法（大津法）,也叫最大类间方差法，它是图像处理领域最经典、最常用的自动阈值分割算法之一，核心思想是 “让前景和背景的差异最大化”，而非简单平衡两类均值。

Otsu阈值法的核心逻辑

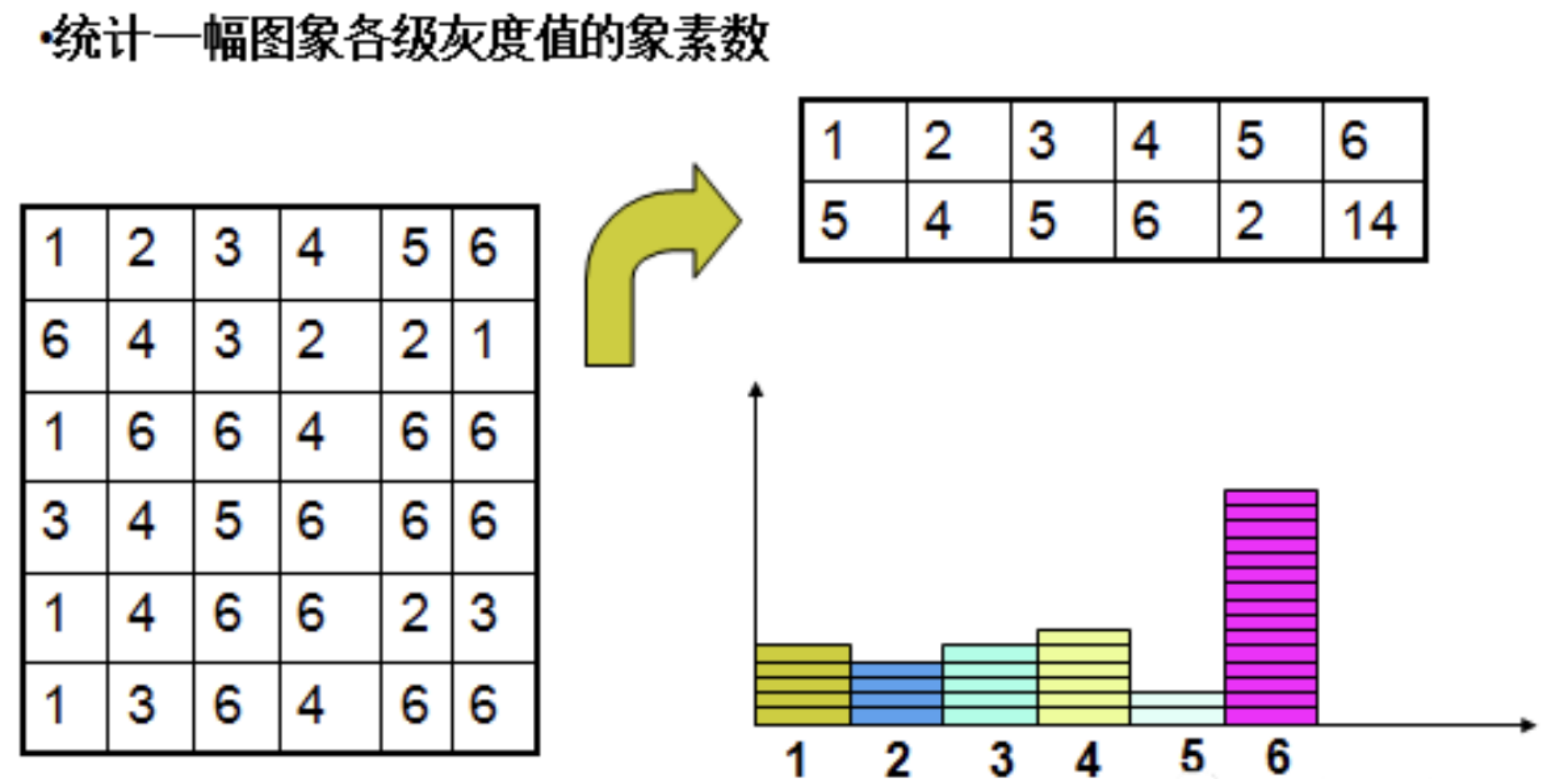
分析直方图：先统计图像中每个灰度级（0~255）出现的频率（比如灰度值50的像素有多少个，灰度值100的像素有多少个）。
遍历所有可能的阈值：从灰度值0到255，依次假设每个灰度值作为候选阈值（比如先试试T=50，再试T=51，直到T=255）。
对每个阈值，把像素分成两类：
一类是灰度值 ≤ 阈值的像素（通常是背景）；
另一类是灰度值 > 阈值的像素（通常是前景）。
计算每组阈值下的“类间方差”：衡量这两类像素的灰度差异有多大。
选方差最大的阈值：当某个阈值对应的类间方差达到最大值时，说明用这个阈值分割后，前景和背景的区分最明显，这就是我们要找的最佳阈值！👍

补充： 👇

以最佳阈值将图像的灰度直方图分割成两部分，使两类之间的方差取最大值，即分离性最大。此算法利用了最小二乘法原理。
编程的时候可以使用穷尽法，让阈值T从0到L-1，找到方差最大的T值，即为最佳阈值。

案例代码

import numpy as np
import cv2
from matplotlib import pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负

# 基本全局阈值法
def basic_global_thresholding(Img,T0=0.1): #输入的图像要求为灰度图像
    '''
    :param Img: 需进行全阈值分割的图像
    :param T0: 迭代终止容差，当相临迭代得到的阈值差小于此值，则终止迭代
    :return: 全阈值
    '''
    G1 = np.zeros(Img.shape, np.uint8)  # 定义矩阵分别用来装被阈值T1分开的两部分
    G2 = np.zeros(Img.shape, np.uint8)
    T1 = np.mean(Img)
    diff=255
    while(diff>T0):
        _,G1=cv2.threshold(Img,T1,255,cv2.THRESH_TOZERO_INV) #THRESH_TOZERO	超过thresh的像素不变, 其他设为0
        _,G2=cv2.threshold(Img,T1,255,cv2.THRESH_TOZERO)
        garray1 = np.array(G1)
        garray2 = np.array(G2)
        loc1 = np.where(garray1>0.001)  #可以对二维数组操作
        loc2 = np.where(garray2 > 0.001)
        # g1 = list(filter(lambda a: a > 0, G1.flatten()))#只能对一维列表筛选，得到的是一个筛选对象
        # g2 = list(filter(lambda a: a > 0, G2.flatten()))
        ave1=np.mean(garray1[loc1])
        ave2=np.mean(garray2[loc2])
        T2=(ave1+ave2)/2.0
        diff=abs(T2 - T1)
        T1=T2
    return T2
# 直方图
def histogram(image):
    (row, col) = image.shape
    #创建长度为256的list
    hist = [0]*256
    for i in range(row):
        for j in range(col):
            hist[image[i,j]] += 1
    return hist



# 案例1
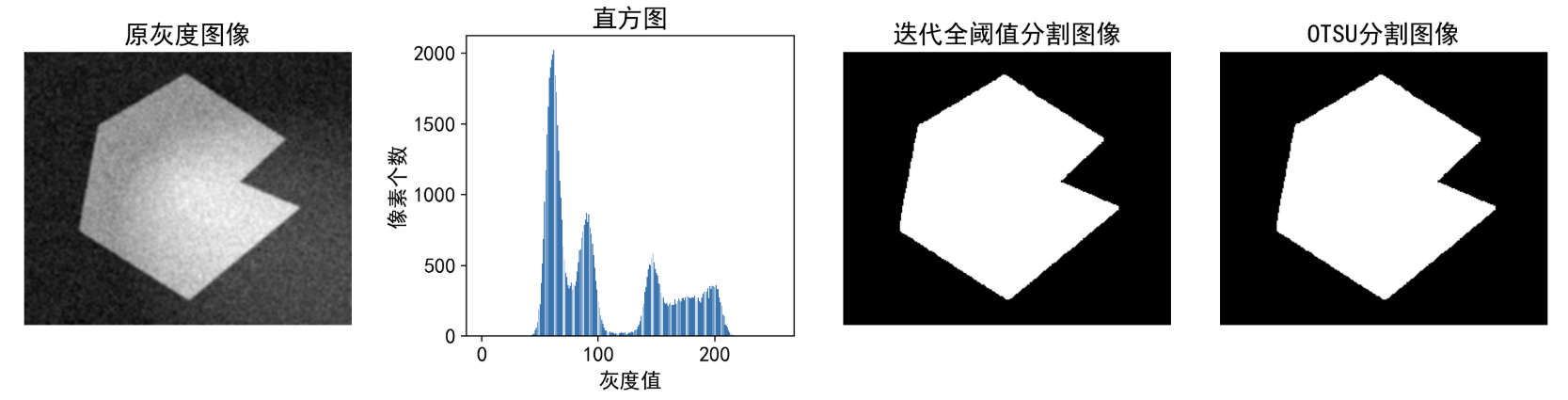
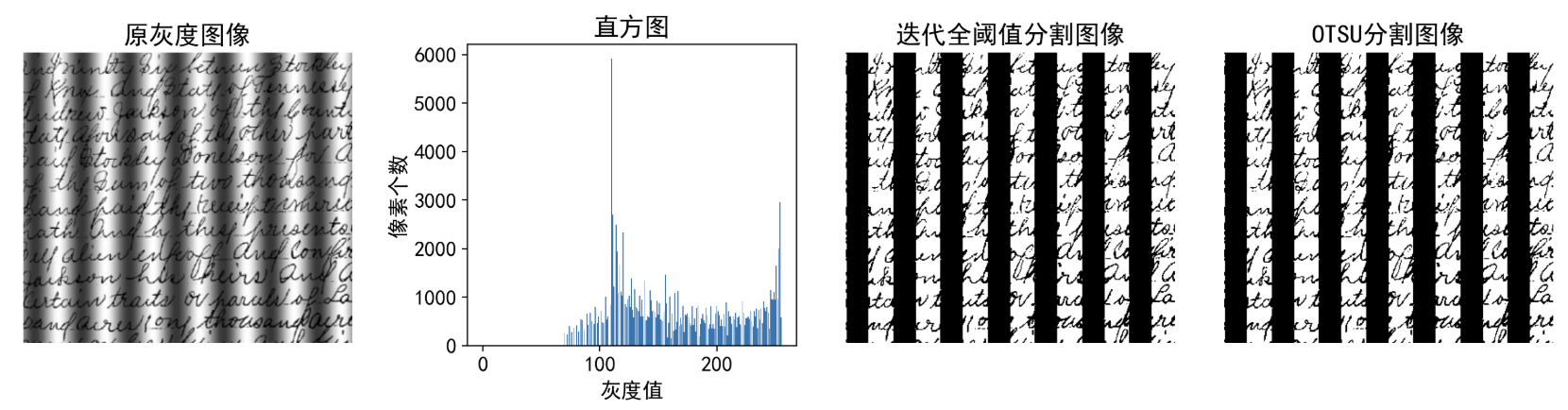
img = cv2.imread(r'./img/paopao.jpg',0)

#案例2 将上面的注释 试试这个 叠加噪声和不均光照试试
# img22 = cv2.imread(r'./img/ch08-4(a).jpg',0) # 读取图像，0表示读取为灰度图像
# # 添加不均匀光照
# img_uneven222 = addNonUniformIllumination(img22.copy())
# # 添加高斯噪声 
# img = addGaussianNoise(img_uneven222, 0, 0.05)
# #平滑一下
# img=cv2.blur(img,(3,3)) 

# 案例3 将上面的注释，试试这个
# img = cv2.imread(r'./img/ch11-01.png',0) # 读取图像，0表示读取为灰度图像

T2=basic_global_thresholding(img,T0=0.1) # 调用全局阈值分割函数，T0为迭代终止容差，当相临迭代得到的阈值差小于此值，则终止迭代
_,img_result=cv2.threshold(img,T2,255,cv2.THRESH_BINARY) # ,_为阈值，img_result为分割结果，255为最大值，THRESH_BINARY为二值化
_,img_otsu=cv2.threshold(img,128,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU) # Otsu阈值分割，128为初始阈值，255为最大值，THRESH_OTSU为Otsu阈值分割

plt.figure(figsize=(15,5))
plt.rcParams.update({"font.size":14})
plt.axes([0.0, 0.1, 0.2, 0.8])
plt.title("原灰度图像")
plt.axis("off")
plt.imshow(img,cmap="gray")
plt.axes([0.27, 0.23, 0.2, 0.55])
plt.title("直方图")
h1=histogram(img)
plt.bar(range(256),h1)
plt.xlabel("灰度值")
plt.ylabel("像素个数")
plt.axes([0.5, 0.1, 0.2, 0.8])
plt.title("迭代全阈值分割图像")
plt.axis("off")
plt.imshow(img_result,cmap="gray")
plt.axes([0.73, 0.1, 0.2, 0.8])
plt.title("OTSU分割图像")
plt.axis("off")
plt.imshow(img_otsu,cmap="gray")
plt.show()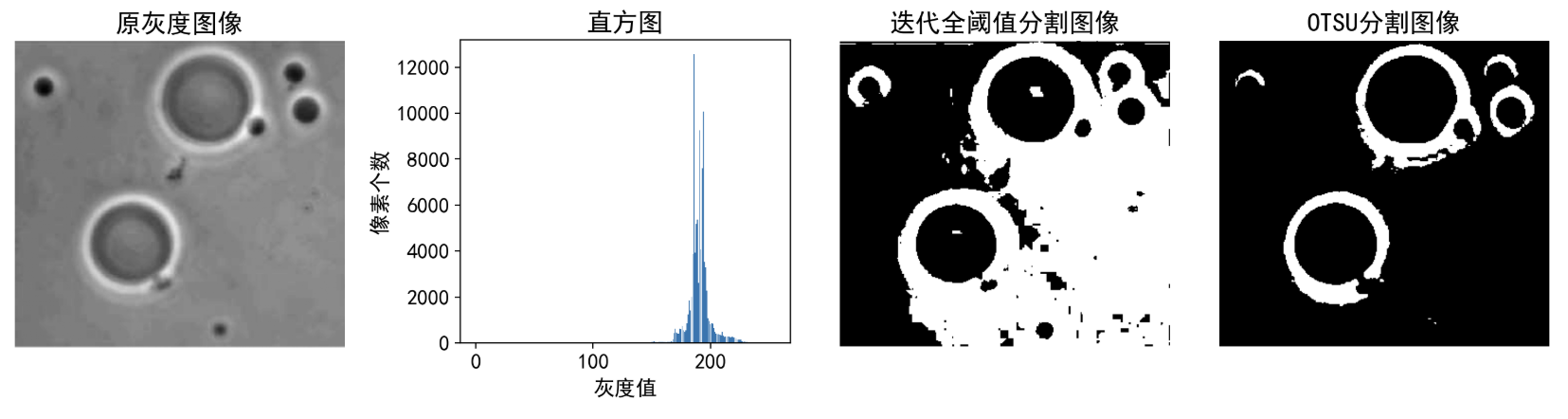

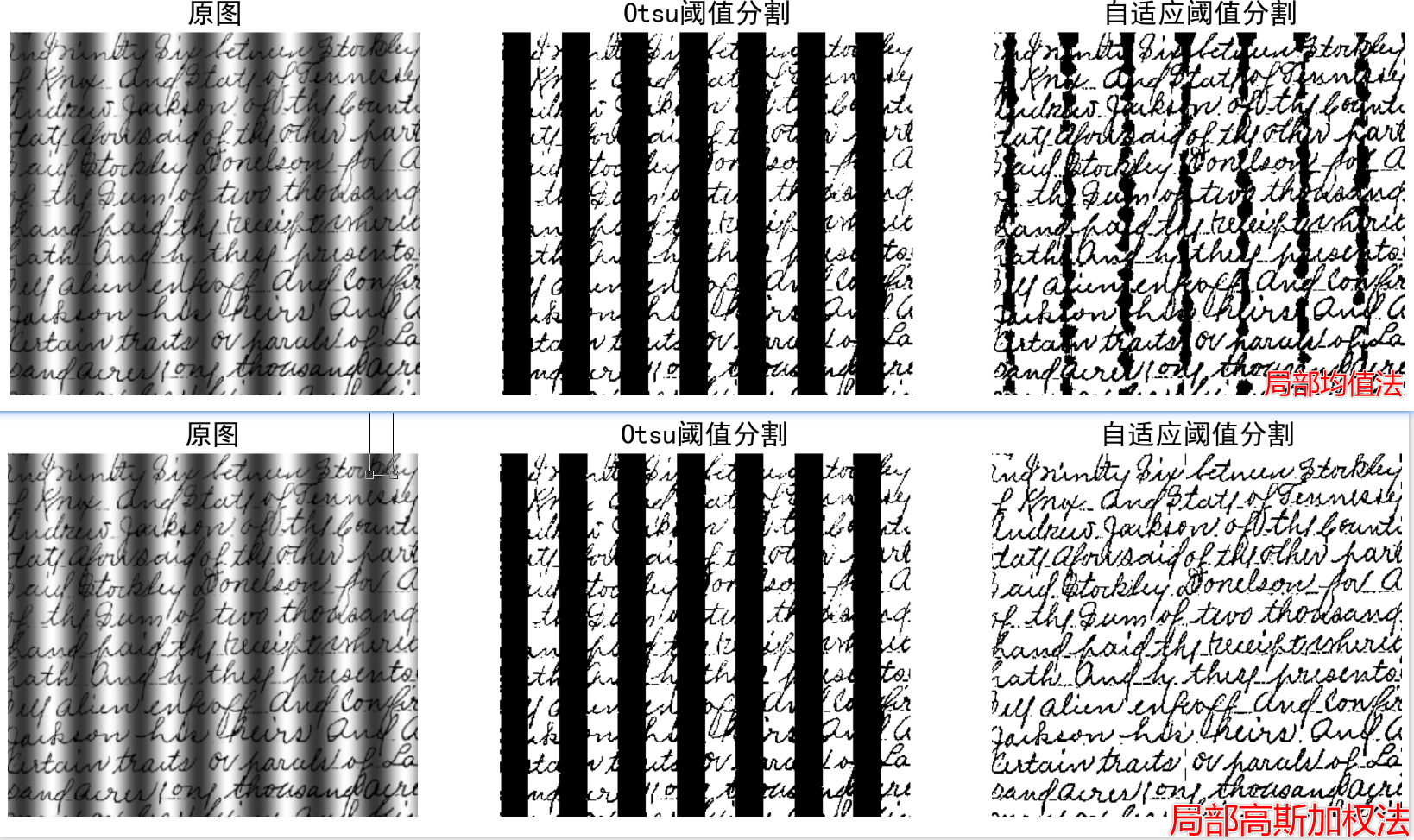
3.2 移动平均阈值法

前言

定义

1.背景和定义

前面2种方法都是全局阈值法，它们的阈值是通过迭代计算得到的，但它们的计算过程是基于全局的，无法处理局部变化。

但在实际应用中，许多图像并不满足这些理想条件”,比如:👇

拍摄的文档可能存在光照不均（一侧亮、一侧暗）
工业检测中的零件可能因表面反光导致局部灰度突变
医学图像中器官与周围组织的灰度差异可能随区域变化。

这时，若用全局统一的阈值分割，会出现“某些区域分割准确，另一些区域却完全错误 ”的问题（例如：亮区文字被误判为背景，暗区背景被误判为目标）。

那么，有没有一种方法能根据图像不同区域的灰度特点，动态调整局部阈值，从而适应复杂光照或灰度变化的场景呢？

答案就是本节要介绍的移动平均阈值法（Moving Average Thresholding），它是一种局部自适应阈值分割技术，核心思想是：通过滑动窗口计算局部区域的平均灰度，动态生成该区域的阈值，实现“哪里亮哪里调高阈值，哪里暗哪里调低阈值”的智能分割。

2.移动平均阈值法的核心逻辑 👇

划分局部区域 ：把整张图片分成许多小的“窗口”（可以是固定大小的方块，比如15×15像素，也可以是滑动的窗口），每个窗口覆盖图像的一小部分。
计算局部平均灰度 ：对每个小窗口内的所有像素，计算它们的灰度平均值（即该区域的“整体明暗程度”）。
动态生成局部阈值 ：根据局部平均灰度，调整该窗口的阈值（例如：窗口较亮时，阈值适当提高，避免把亮背景误判为目标；窗口较暗时，阈值适当降低，避免把暗目标误判为背景）。
常见的调整方式 ：直接用局部平均灰度作为阈值，或在其基础上加减一个固定偏移量（如阈值 = 局部平均灰度 ± 常数）。
逐区域分割 ：对每个小窗口内的像素，用该窗口对应的局部阈值进行二值化（例如：像素灰度 ≥ 局部阈值 → 前景；像素灰度 < 局部阈值 → 背景）。
合并结果 ：将所有小窗口的分割结果拼接起来，形成整张图片的最终二值图像。

举个例子帮助理解
假设有一张扫描的文档图片，左侧因光源直射较亮（文字灰度约180_{200），右侧因阴影较暗（文字灰度约100}120），背景左侧灰度约220_{240，右侧灰度约80}100。

移动平均阈值法：将图片分成多个15×15的小窗口后，右侧亮区的窗口平均灰度约210，动态阈值可能设为200（文字180_{200仍高于阈值，被分为前景）；左侧暗区的窗口平均灰度约90，动态阈值可能设为80（文字100}120高于阈值，被分为前景）。最终，左右两侧的文字都能被准确分割，而背景被正确排除。

👇 👇
在OpenCV中，移动平均阈值法和自适应阈值法核心思想相似（都是局部自适应分割），但OpenCV官方库中没有直接提供“移动平均阈值法”的现成函数，而提供了专门的 cv2.adaptiveThreshold()函数来实现自适应阈值法。因此，两者的主要区别体现在：一个是需要手动实现（或自行封装逻辑），另一个是OpenCV原生支持。

import numpy as np
import cv2
from matplotlib import pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负


img0 = cv2.imread(r'./img/light_circle.jpg',0)
# 案例2 将上面的注释，试试这个
img0 = cv2.imread(r'./img/ch11-01.png',0) 

# 案例3 将上面的注释，试试这个

# img0 = cv2.imread(r'./img/Fig0926(a)(rice).tif',0) 



_,img_seg=cv2.threshold(img0,128,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
# 自适应阈值分割 ADAPTIVE_THRESH_MEAN_C 为局部均值法，ADAPTIVE_THRESH_GAUSSIAN_C为局部高斯加权法，THRESH_BINARY为二值化，kernalSize为窗口大小，6为偏移量
kernalSize=19
img_seg_adapt = cv2.adaptiveThreshold(img0, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, kernalSize, 6) 
# 自适应阈值分割 ADAPTIVE_THRESH_MEAN_C 为局部均值法，ADAPTIVE_THRESH_GAUSSIAN_C为局部高斯加权法，THRESH_BINARY为二值化，kernalSize为窗口大小，6为偏移量
plt.figure(figsize=(15,5))
plt.subplot(131)
plt.imshow(img0,cmap="gray")
plt.axis("off")
plt.title("原图")

plt.subplot(132)
plt.imshow(img_seg,cmap="gray")
plt.axis("off")
plt.title("Otsu阈值分割")

plt.subplot(133)
plt.imshow(img_seg_adapt,cmap="gray")
plt.axis("off")
plt.title("自适应阈值分割")
plt.show()