傅里叶变换

yange大约 11 分钟数字图像处理数字图像处理

1. 傅里叶级数和

前言

定义

1.为什么图像处理需要傅里叶变换？

当我们处理数字图像时，常常需要分析图像中的各种频率成分。傅里叶变换就像是一副"数学眼镜"，能让我们看到图像中不同频率的成分分布。例如：

高频部分：代表图像的边缘、细节和噪声
低频部分：代表图像的整体结构和大致轮廓

这样，我们就可以根据图像的不同频率成分，对图像进行增强、锐化、模糊等处理，从而实现图像的增强、锐化、模糊等效果。

比如，我们可以通过高通滤波器来增强图像的边缘和细节，通过低通滤波器来模糊图像的边缘和细节。

那怎样才能获取这些频率成分呢？这就需要用到傅里叶变换。

在讲解傅里叶变换之前，我们先来了解一下傅里叶级数。 👈 👈

2. 从周期现象到傅里叶级数

在讲解知识之前，我们先介绍下一个人，傅里叶。

Fourier出生于1768年，是法国数学家、物理学家。他发明了傅里叶级数。后人在他研究成果的基础上，又对傅里叶级数进行了改进，提出了傅里叶变换。

傅里叶变换是现代工程中最重要的数学理论之一

好了，接下来我们就来讲解傅里叶级数。👇 👇

1. 基本概念
想象一个复杂的音乐和弦，它其实是由多个简单的正弦波组成的。

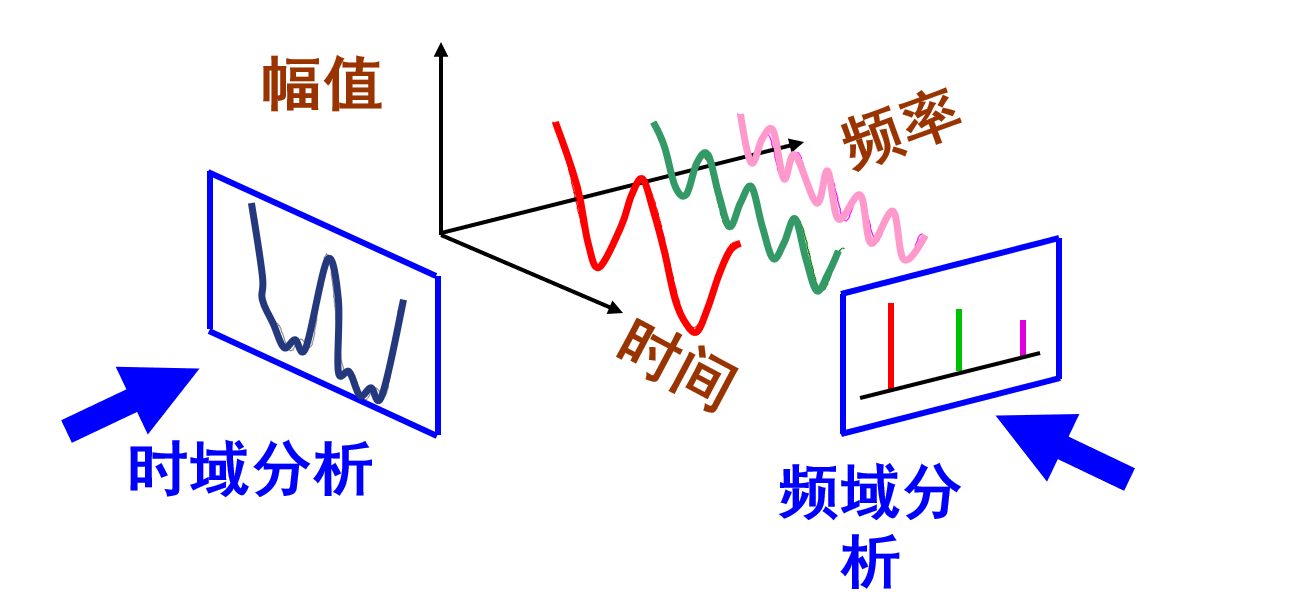
傅里叶级数的核心思想就是：任何周期信号都可以表示为不同频率的正弦和余弦函数的和。 👈 👈

如果不理解，可以看下图：

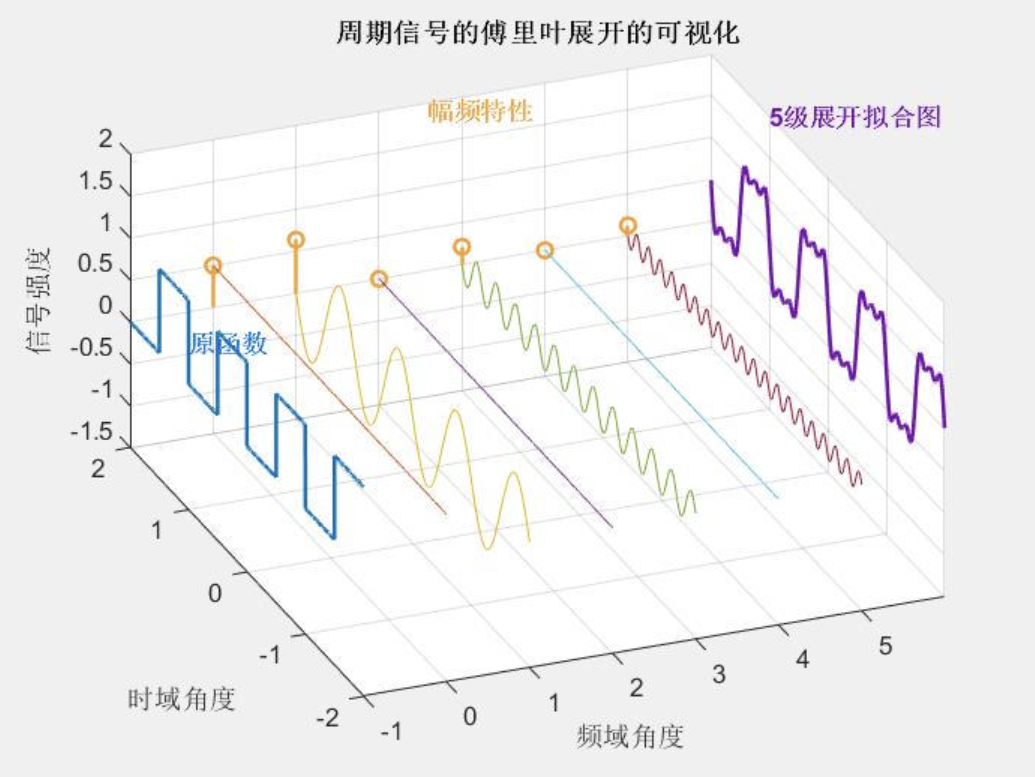
如果还不理解，可以通过可视化的方式展示：https://www.jezzamon.com/fourier/zh-cn.html 👈 👈

2. 傅里叶级数公式

对于周期为T的函数f(t)，可以表示为：

f(t) = a₀/2 + Σ[aₙcos(nω₀t) + bₙsin(nω₀t)]

其中：
ω₀=2π/T 是基频
aₙ和bₙ是各频率成分的系数
n=1,2,3,...表示谐波次数



复数形式的傅里叶级数公式为：

f(t) = Σ cₙe^(jnω₀t)

其中cₙ是复数系数，包含了幅度和相位信息。

相位指的是正弦函数的初始相位，幅度指的是正弦函数的振幅。<-----  记住这个词汇，后面会用到相位谱，是图像的结构蓝图，表示了图像中不同频率成分的结构分布
幅度指的是正弦函数的振幅。<-----  是图像的"能量地图"，表示了图像中不同频率成分的能量分布

结合上述的可视化页面，我们对傅里叶级数有了初步的了解，发现傅里叶级数就像一台"周期信号分析仪" ：

只能处理严格周期性的信号（如完美的心电图、交流电）
要求信号必须无限重复（周期T固定）

而实际问题：

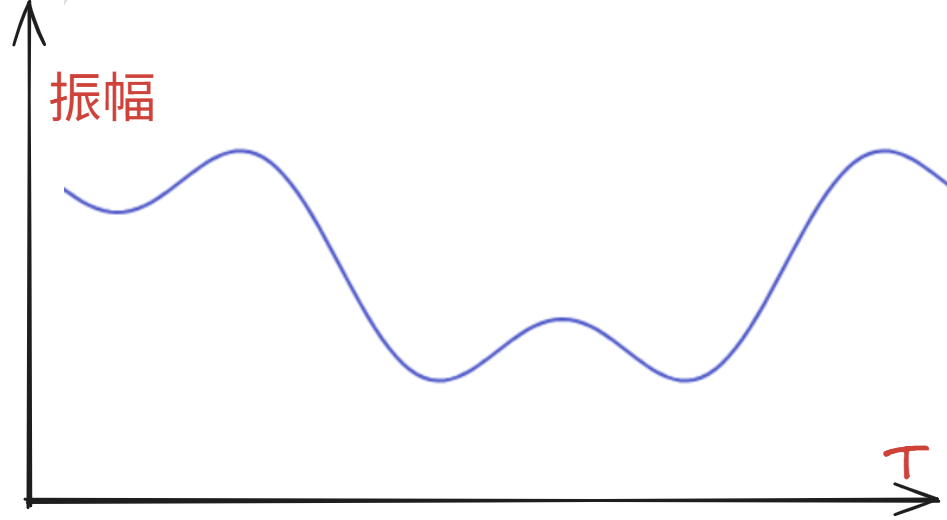
现实中大多数信号是非周期的（如语音信号、图像、突发脉冲）
即使近似周期信号，也常有微小变化（如实际心电图每次心跳略有不同）如下图👇

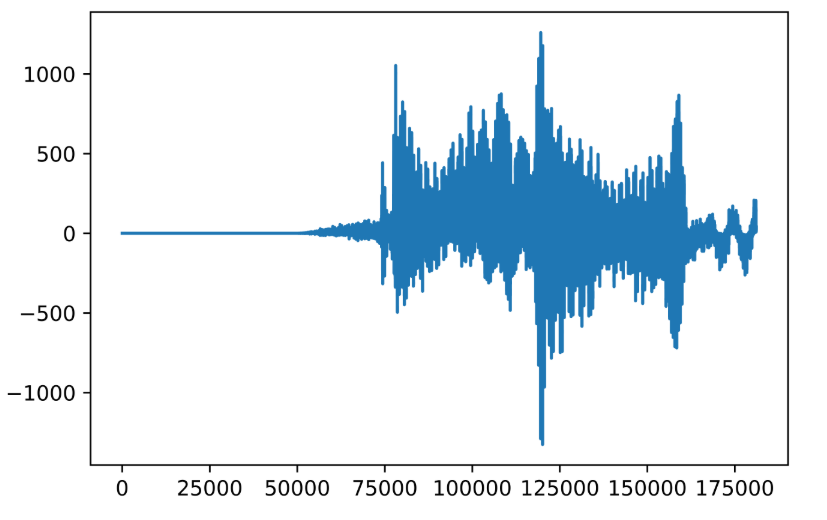
而傅里叶级数无法处理这种情况，😢 😢 所以我们需要用到傅里叶变换。:

3. 从傅里叶级数到傅里叶变换

3. 1. 非周期信号的扩展

当周期T→∞ 扩展无穷时，我们可以认为信号是无限重复的，这样就可以用傅里叶级数来分析信号了，离散的频率nω₀变为连续的频率ω，求和变为积分，这就是傅里叶变换：

F(ω) = ∫ f(t)e^(-jωt) dt /

f(t)是时域信号，F(ω)是频域信号
上式是从时域到频域的变换，称为傅里叶变换

3.2. 直观理解

傅里叶变换可以看作是一个"信号成分分析器"：

输入：时域信号（如随时间变化的电压）
输出：频域表示（各频率成分的强度和相位）

那对于数字图像的增强，我们可以采用傅里叶变换将图像转为频域图像，然后对频域图像进行处理，最后将处理后的频域图像转为时域图像。

F(ω) = ∫ f(t)e^(-jωt) dt /

f(t)是时域信号，F(ω)是频域信号
上式是从时域到频域的变换，称为傅里叶变换

逆变换：

f(t) = (1/2π) ∫ F(ω)e^(jωt) dω

上式是从频域到时域的变换，称为傅里叶逆变换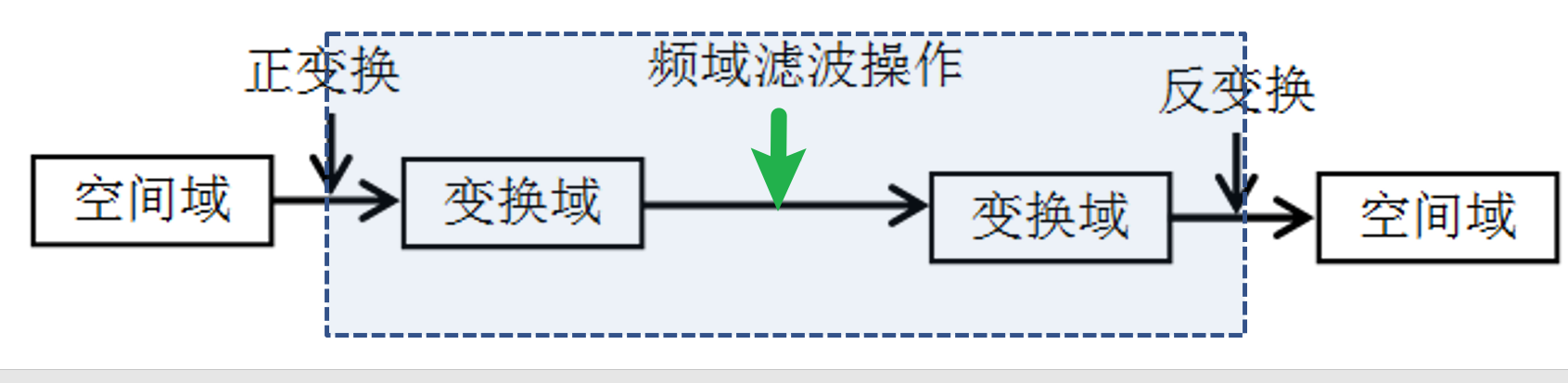

2. 离散傅里叶变换

前言

定义

1. 为什么数字图像处理要用二维离散傅里叶变换尼？

傅里叶变换有多种不同的变体形式，如连续时间傅里叶变换、离散时间傅里叶变换等，在数字信号处理中，处理的信号是随着时间变化的时域信号，其自变量为t；而图像中是二维随空间坐标变化的灰度值，属于空域信号，其自变量为x和y。因此图像处理通常使用的是二维离散傅里叶变换（DFT），信号在空间域和频率域上都呈现离散形式。

数据结构维度： 👇

一维信号
- 时域：单一时间轴上的幅度变化（如音频波形）
- 频域：仅反映时间方向的频率成分

二维图像
- 空间域：像素在x和y两个方向上的强度分布
- 频域：需要同时捕获水平和垂直方向的空间频率

案例展示：👇

import cv2
import numpy as np
import matplotlib.pyplot as plt
from scipy import misc

# 尝试读取图像（添加错误处理）
img = cv2.imread('./img/cameraman.bmp', 0)

# 检查图像尺寸
if img.size == 0:
    raise ValueError("加载的图像为空，请检查文件路径")

# 计算DFT
dft = np.fft.fft2(img)
dft_shift = np.fft.fftshift(dft)  # 将低频移到中心
a
# 计算幅度谱（加1避免log(0)）
magnitude_spectrum = 20 * np.log(np.abs(dft_shift) + 1e-6)

# 使用matplotlib显示（比cv2.imshow更稳定）
plt.figure(figsize=(12, 6))
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('原始图像'), plt.axis('off')
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('幅度谱'), plt.axis('off')
plt.tight_layout()
plt.show()

频域滤波的本质是通过修改图像的频率成分来实现特定处理效果。当图像转换到频域后，我们实际上获得了一幅"频谱地图"，其中：

坐标位置：每个点(u,v)代表特定的空间频率（u是水平方向，v是垂直方向）
- 靠近中心：低频成分（图像整体明暗）
- 远离中心：高频成分（边缘和细节）
点的亮度：表示该频率成分的强度
点的相位：记录频率成分的空间位置信息

3. OpenCV中的傅里叶变换

OpenCV中的傅里叶变换

定义

import numpy as np
import cv2
import matplotlib.pyplot as plt
%matplotlib inline

# 读取图像并转为浮点型
img = cv2.imread(r'./img/peppers.bmp', 0).astype(np.float32)  # 关键修改1：转为float32

if img is None:
    raise FileNotFoundError("无法加载图像，请检查路径")

# 傅里叶变换
dft = np.fft.fft2(img)
dft_shift = np.fft.fftshift(dft)  # 低频移到中心

# 计算幅值谱和相位谱
magnitude_spectrum = 20 * np.log(1 + np.abs(dft_shift))
phase_spectrum = np.angle(dft_shift)  # 获取相位信息

# 提取幅度谱和相位谱
magnitude = np.abs(dft_shift)
phase = np.angle(dft_shift)

## 注意啦，这里有2种重构方式！！！！ 可以自行尝试
# 重构图像（从中心化频谱）
# reconstructed = np.fft.ifft2(np.fft.ifftshift(dft_shift)).real
# 幅值谱和相位谱重构图像
reconstructed = np.fft.ifft2(np.fft.ifftshift(magnitude * np.exp(1j*phase))).real
# 可视化
plt.figure(figsize=(15, 10))

plt.subplot(231), plt.imshow(img, cmap='gray')
plt.title('原始图像'), plt.axis('off')

plt.subplot(232), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('幅值谱'), plt.axis('off')

plt.subplot(233), plt.imshow(phase_spectrum, cmap='gray')
plt.title('相位谱'), plt.axis('off')

plt.subplot(234), plt.imshow(reconstructed, cmap='gray')
plt.title('重构图像'), plt.axis('off')

# 幅值谱和相位谱互换实验
mag_only = np.abs(dft_shift) * np.exp(1j * 0)  # 仅保留幅值
phase_only = 1 * np.exp(1j * np.angle(dft_shift))  # 仅保留相位

recon_mag = np.fft.ifft2(np.fft.ifftshift(mag_only)).real
recon_phase = np.fft.ifft2(np.fft.ifftshift(phase_only)).real

plt.subplot(235), plt.imshow(recon_mag, cmap='gray')
plt.title('仅用幅值重构'), plt.axis('off')

plt.subplot(236), plt.imshow(recon_phase, cmap='gray')
plt.title('仅用相位重构'), plt.axis('off')

plt.tight_layout()
plt.show()

总结记忆要点：👇

幅度谱是图像的"能量地图"（回答"有多少"）
相位谱是图像的"结构蓝图"（回答"在哪里"）
只有幅度 → 模糊的色块--失去所有结构信息，呈现无意义的能量分布
只有相位 → 可识别的轮廓--保留边缘和结构特征，但失去明暗对比

重要发现：

仅用相位重构的图像仍能保留主要边缘特征
仅用幅值重构的图像几乎丢失所有结构信息
这证明相位谱在图像重建中比幅值谱更重要

4. 傅里叶变换的应用

傅里叶变换的应用

定义

1. 理想低通滤波器

存在一个截止频率 D0, 当 D(u,v) ≤ D0 时，低通滤波器的传递函数 H(u,v) 为 1(表示允许通过)，否则为 0(表示衰减)。

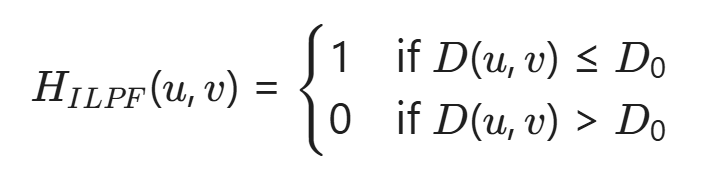
D(u,v)表示从频谱中心到像素 (u,v) 的距离。H(u,v) 表示从像素 (u,v) 到频谱中心的衰减程度。

简单案例：圆形理想低通

想象频谱是一个平面，中心是低频。ILPF 就像一个中心在频谱中心、半径为 D0 的圆。圆内的低频全通过，圆外的高频全挡住

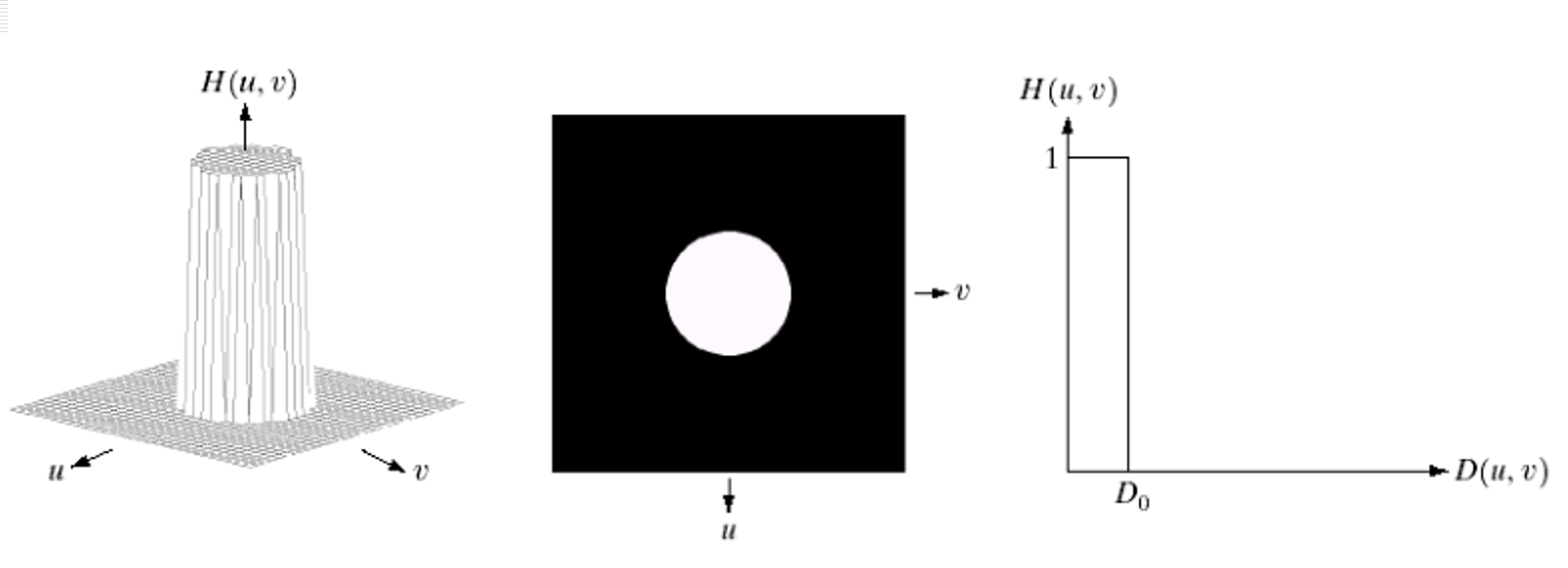
平滑效果与问题： 👇

优点： 理论上能完全保留截止频率内的低频，实现理想平滑。
致命缺点： 振铃效应 (Ringing Artifact)。由于理想阶跃在频域的陡峭截止，逆变换到空域会产生震荡的波纹，导致图像边缘产生模糊的同心圆或波纹。(如下图) 👇
应用场景： 几乎不用于实际图像处理，主要用于理论教学。

2. 理想高通滤波器

理想高通滤波器 与理想低通滤波器相反，存在截止频率 D0，频率距离 D(u,v)≥D0 的高频分量全部通过，否则全部滤除。

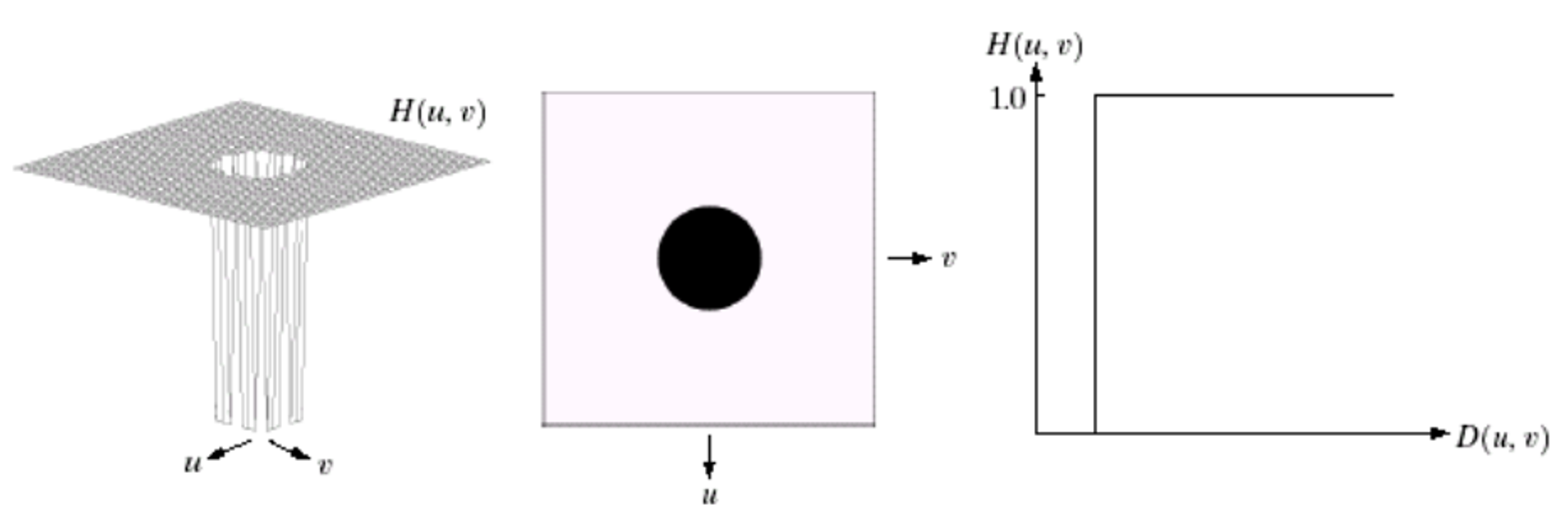
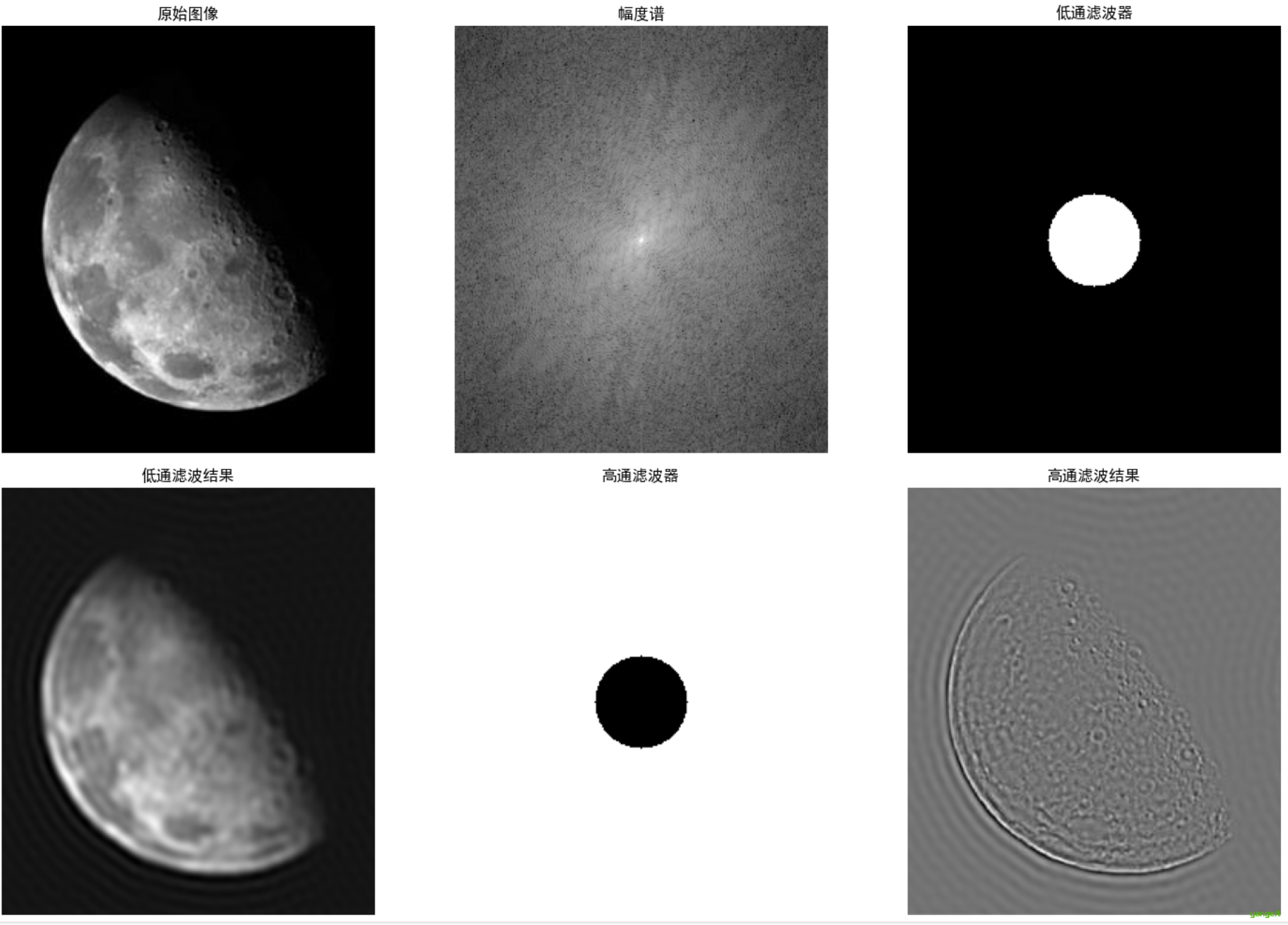
3. 代码演示 👇

import numpy as np
import cv2
import matplotlib.pyplot as plt

# 读取图像并转为灰度
img = cv2.imread('./img/moon.jpg', 0).astype(np.float32)
if img is None:
    # 如果找不到图像，创建测试图
    img = np.zeros((256,256))
    img[100:156, 100:156] = 255  # 白色方块
    print("使用模拟图像替代")
else:
    # 确保图像是2D的灰度图像
    if len(img.shape) == 3:
        img = img[:, :, 0]  # 取第一个通道
    elif len(img.shape) > 2:
        # 如果是多通道图像，转换为灰度
        img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY).astype(np.float32)

print(f"图像形状: {img.shape}, 维度: {len(img.shape)}")  # 调试信息

# 傅里叶变换
dft = np.fft.fft2(img) # 获取频域表示
dft_shift = np.fft.fftshift(dft) # 低频移到中心


def create_filter(shape, center, radius, filter_type='lowpass'):
    """创建圆形滤波器"""
    # 确保shape是二维的
    if len(shape) == 3:
        rows, cols = shape[:2]
    else:
        rows, cols = shape
    
    crow, ccol = center # 获取中心坐标
    mask = np.zeros((rows, cols), np.float32) # 创建掩码
    y, x = np.ogrid[:rows, :cols] # 创建网格
    
    # 计算距离矩阵
    dist_from_center = np.sqrt((x - ccol)**2 + (y - crow)**2) #
    
    if filter_type == 'lowpass':# 低通滤波器
        mask[dist_from_center <= radius] = 1 # 在半径内设为1
    elif filter_type == 'highpass':# 高通滤波器
        mask[dist_from_center > radius] = 1 # 在半径外设为1
    elif filter_type == 'bandpass':# 带通滤波器
        # 对于带通滤波器，radius应该是一个包含两个元素的列表/元组 [inner_radius, outer_radius]
        if isinstance(radius, (list, tuple)) and len(radius) == 2:
            mask[np.logical_and(dist_from_center >= radius[0], 
                               dist_from_center <= radius[1])] = 1
        else:
            raise ValueError("带通滤波器需要指定半径范围 [inner_radius, outer_radius]")
    
    return mask  # 确保函数在所有分支都有返回


# 参数设置
# 安全地获取图像尺寸
if len(img.shape) == 2:
    rows, cols = img.shape
elif len(img.shape) == 3:
    rows, cols = img.shape[:2]
else:
    rows, cols = img.shape[0], img.shape[1]

center = (rows//2, cols//2) # 设置中心坐标
radius = min(rows, cols) // 8  # 动态计算半径，使用图像最小尺寸的1/8

print(f"中心坐标: {center}, 半径: {radius}")  # 调试信息

# 创建低通滤波器
lowpass_mask = create_filter(img.shape, center, radius, 'lowpass')

# 应用滤波 
filtered_dft = dft_shift * lowpass_mask # 
lowpass_img = np.fft.ifft2(np.fft.ifftshift(filtered_dft)).real


# 创建高通滤波器
highpass_mask = create_filter(img.shape, center, radius, 'highpass')

# 应用滤波
filtered_dft = dft_shift * highpass_mask
highpass_img = np.fft.ifft2(np.fft.ifftshift(filtered_dft)).real


plt.figure(figsize=(15,10))
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

# 原始图像和频谱
plt.subplot(231), plt.imshow(img, cmap='gray')
plt.title('原始图像'), plt.axis('off')

magnitude_spectrum = 20*np.log(1+np.abs(dft_shift))
plt.subplot(232), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('幅度谱'), plt.axis('off')

# 低通滤波结果
plt.subplot(233), plt.imshow(lowpass_mask, cmap='gray')
plt.title('低通滤波器'), plt.axis('off')

plt.subplot(234), plt.imshow(lowpass_img, cmap='gray')
plt.title('低通滤波结果'), plt.axis('off')

# 高通滤波结果
plt.subplot(235), plt.imshow(highpass_mask, cmap='gray')
plt.title('高通滤波器'), plt.axis('off')

plt.subplot(236), plt.imshow(highpass_img, cmap='gray')
plt.title('高通滤波结果'), plt.axis('off')

plt.tight_layout()
plt.show()