边缘检测、模板匹配和霍夫变换

yange大约 13 分钟数字图像处理数字图像处理

边缘检测

1. 边缘检测的基本概念

前言

定义

1. 什么是边缘检测？

边缘检测是图像处理和计算机视觉中的基本问题，边缘检测的⽬的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。边缘的表现形式如下图所示：

图像边缘检测大幅减少了数据量，并且剔除了可以认为不相关的信息，保留了图像重要的结构属性。

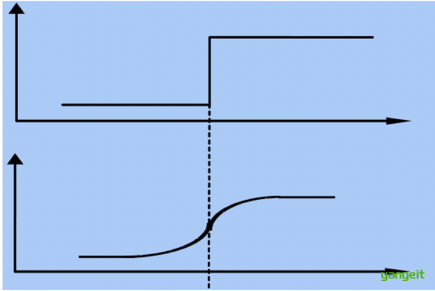
想象一下一幅从左到右亮度逐渐增加的图像，它的灰度变化曲线是平缓的斜坡。而在一个物体的边缘处，灰度会有一个突然的跳变，曲线会变得很陡峭。

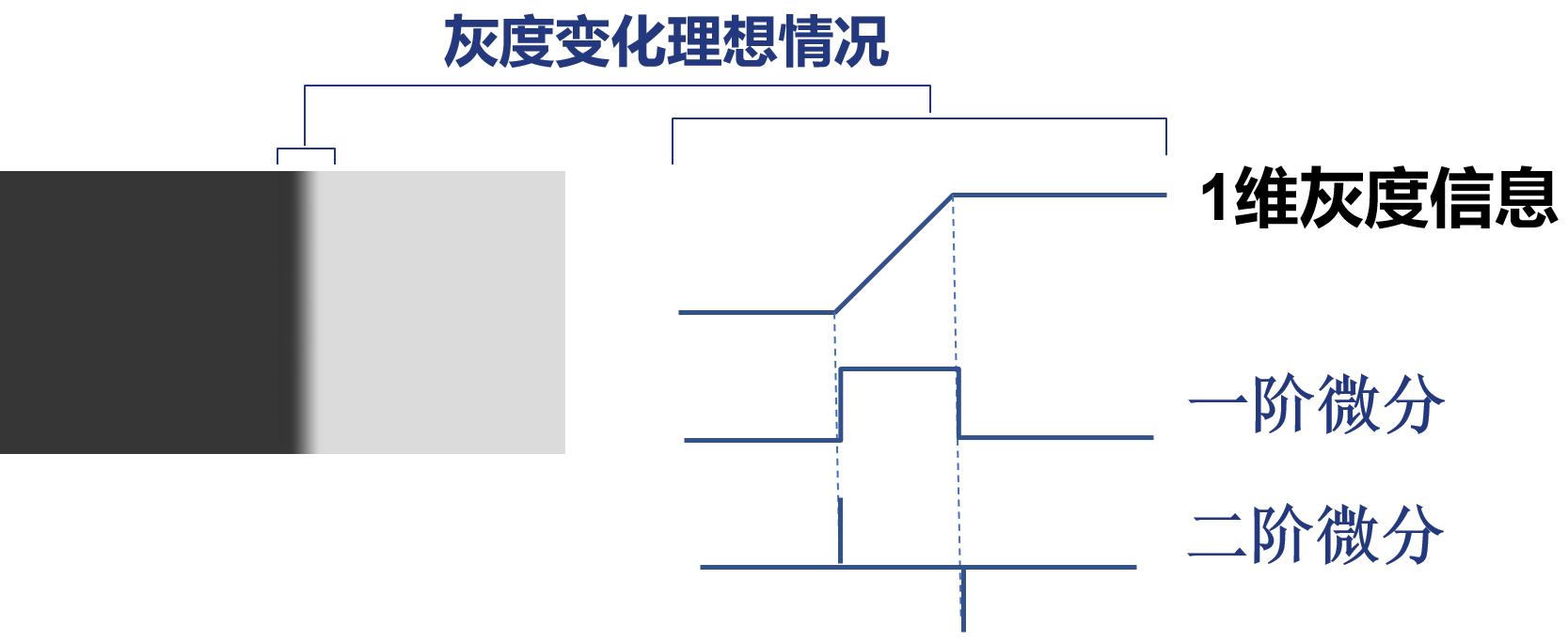
一阶微分：衡量的是变化的速度。在平缓区域，一阶微分值接近0；在陡峭的边缘，一阶微分值会很大。所以，一阶微分会产生一个很宽的“边缘”。
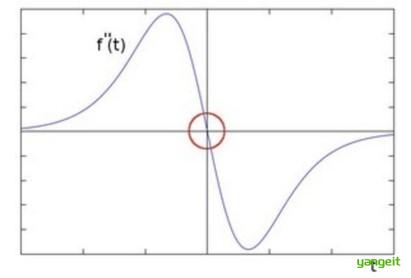
二阶微分：衡量的是变化速度的变化率，也就是曲线的斜率变化。在平缓区域，二阶微分值为0；在灰度跳变的边缘起点（从平缓变陡峭），二阶微分会产生一个正脉冲；在边缘的终点（从陡峭变平缓），会产生一个负脉冲。这意味着，二阶微分会产生一个双边缘，并且能够突出灰度变化的方向。

有许多方法用于边缘检测，它们的绝大部分可以划分为两类：基于搜索和基于零穿越。

基于搜索：通过寻找图像一阶导数中的最大值来检测边界，然后利用计算结果估计边缘的局部方向，通常采用梯度的方向，并利用此方向找到局部梯度模的最大值。代表算法：Sobel算子。

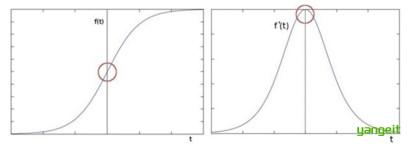
基于零穿越 ：通过寻找图像二阶导数零穿越来寻找边界。代表算法：Laplacian拉普拉斯算子。

2. 边缘检测的常用算子

前言

定义

三大边缘检测算子核心区别对比表

对比维度	Sobel算子	Laplacian算子	Canny算子
数学本质	一阶微分算子（梯度计算： $\nabla f = (G_x, G_y)$ ）	二阶微分算子（二阶导数： $\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$ ）	多阶段复合算子（高斯滤波+一阶微分+非极大值抑制+双阈值）
核心原理	计算像素邻域的亮度变化率（梯度幅值）	检测像素邻域的亮度曲率变化（二阶导数过零点）	先降噪、再找边缘、最后细化+去伪，全流程优化边缘质量
边缘特点	边缘较粗（1-2像素）、连续但不够精细	边缘极细（单像素）、定位精准，但易有双边响应	边缘最细（单像素）、连续光滑、几乎无杂点
抗噪性	⭐⭐⭐☆☆ 较好（核内加权平均抑制噪声）	⭐☆☆☆☆ 差（二阶微分放大高频噪声）	⭐⭐⭐⭐⭐ 优秀（高斯滤波预处理+双阈值过滤伪边缘）
计算复杂度	中等（需两次卷积：X+Y方向）	低（一次卷积）	高（多步骤复合，但OpenCV已高度优化）
参数依赖性	低（仅需选择核大小，通常固定3×3）	低（仅需选择核类型，4邻域/8邻域）	高（需手动调双阈值`threshold1/threshold2`，影响边缘完整性）
典型应用场景	实时视频处理、工业检测、特征提取（需方向信息时）	图像锐化、噪声少的精细结构检测（如扫描文档）	自动驾驶、医学影像、高精度测量（对边缘质量要求严苛的场景）
一句话总结	稳健的“粗边缘检测器”，适合对稳定性要求高的任务	敏感的“细节放大镜”，适合无噪声环境的精细检测	全能的“工业级边缘引擎”，综合性能碾压前两者

案例：👇

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

# ---------------------- 1. 创建简单测试图 ----------------------
# 生成200x200的黑色图
img = np.zeros((200, 200), dtype=np.uint8)

# 画一个白色圆形（圆心(100,100)，半径40）
cv2.circle(img, (100, 100), 40, 255, -1)  # -1表示填充

# ---------------------- 2. 三种边缘检测（超简单） ----------------------
# 方法1：Sobel边缘（简单组合）
sobel_x = cv2.Sobel(img, cv2.CV_8U, 1, 0, ksize=3)
sobel_y = cv2.Sobel(img, cv2.CV_8U, 0, 1, ksize=3)
sobel_edge = cv2.magnitude(sobel_x.astype(float), sobel_y.astype(float))
sobel_edge = np.uint8(sobel_edge)  # 转成图像格式

# 方法2：Laplacian边缘（简单调用）
laplacian_edge = cv2.Laplacian(img, cv2.CV_8U)
laplacian_edge = cv2.convertScaleAbs(laplacian_edge)  # 取绝对值

# 方法3：Canny边缘（一行代码！）
canny_edge = cv2.Canny(img, 50, 150)  # 低阈值50，高阈值150

# ---------------------- 3. 简单对比显示 ----------------------
plt.figure(figsize=(12, 4))

plt.subplot(1, 4, 1)
plt.imshow(img, cmap='gray')
plt.title("原图（白色圆形）")
plt.axis('off')

plt.subplot(1, 4, 2)
plt.imshow(sobel_edge, cmap='gray')
plt.title("Sobel边缘\n（较粗、有杂点）")
plt.axis('off')

plt.subplot(1, 4, 3)
plt.imshow(laplacian_edge, cmap='gray')
plt.title("Laplacian边缘\n（细但有很多杂点）")
plt.axis('off')

plt.subplot(1, 4, 4)
plt.imshow(canny_edge, cmap='gray')
plt.title("Canny边缘\n（细、干净、连续）")
plt.axis('off')

plt.tight_layout()
plt.suptitle("三行代码实现Canny边缘检测（对比Sobel/Laplacian）", fontsize=14, fontweight='bold')
plt.subplots_adjust(top=0.85)
plt.show()

表格关键结论速记

选Sobel：要稳定、怕噪声、求实时 → “宁可边缘粗一点，不能错检漏检”。
选Laplacian：图像干净、要极致细节 → “细节控专属，但得小心噪声捣乱”。
选Canny：要质量、抗干扰、做专业应用 → “预算够（算力/调参）就上Canny，效果不会失望”。

Canny案例 👇

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

# ---------------------- 1. 读取图片并预处理 ----------------------
# 读取图片（替换为你的cat.png路径）
img = cv2.imread('./img/dog.png',0)  

# ---------------------- 2. Canny边缘检测（核心一步） ----------------------
# 自动高斯模糊+Canny检测（阈值可根据图片调整）
edges = cv2.Canny(img, threshold1=50, threshold2=150)  # 低阈值50，高阈值150
# ---------------------- 3. 显示对比结果 ----------------------
plt.figure(figsize=(15, 5))

# 灰度图
plt.subplot(1, 3, 2)
plt.imshow(img, cmap='gray')
plt.title("灰度图（预处理）")
plt.axis('off')
# Canny边缘结果
plt.subplot(1, 3, 3)
plt.imshow(edges, cmap='gray')
plt.title("Canny边缘检测结果")
plt.axis('off')

plt.tight_layout()
plt.suptitle("Canny算子检测猫咪边缘示例", fontsize=16, fontweight='bold')
plt.subplots_adjust(top=0.85)
plt.show()

原图像(I)：需在其中定位与模板匹配的目标区域；
模板(T)：用于与原图像比对的图像块。

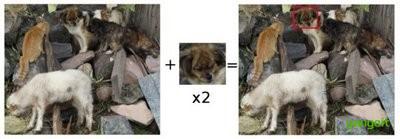
滑动模板图像和原图像进行比对：

以固定大小的模板为“窗口”，在原图像上逐位置滑动，依次计算模板与对应窗口区域的相似度，最终筛选出相似度最高的位置作为匹配结果。

2. 实现

OpenCV提供了模板匹配的函数matchTemplate()，其原型如下：

dst = cv2.matchTemplate(image, templ, method, mask=None)

参数说明：

image：待匹配的原图像；
templ：模板图像；
method：匹配算法；主要有：平方差匹配(cv2.TM_SQDIFF)、相关匹配(cv2.TM_CCORR)、相关系数匹配(cv2.TM_CCORR_NORMED)
- 平方差匹配:利用模板与图像之间的平方差进⾏匹配，最好的匹配是0，匹配越差，匹配的值越⼤。
- 相关匹配:利用模板与图像之间的乘积进⾏匹配，最好的匹配是1，匹配越差，匹配的值越⼩，
- 相关系数匹配:利用模板与图像之间的相关系数进⾏匹配，最好的匹配是1，匹配越差，匹配的值越⼩，-1表示完全不相关。
mask：掩码图像，可选参数。

完成匹配后，使用cv.minMaxLoc()方法查找极值位置即可。若使用平方差作为比较方法，则最小值位置是最佳匹配位置；其他方法则取最大值位置为最佳匹配位置。

案例如下：

在该案例中，载⼊要搜索的图像和模板，图像如下所示：

模板如下所示：
wlwz_1

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt

# 1. 图像和模板读取（确保路径下存在目标文件）
img = cv.imread('./img/wlwz.jpg')       # 原图像（BGR格式）
template = cv.imread('./img/wlwz_1.jpg')  # 模板图像（需与原图像通道数一致）

if img is None or template is None:
    raise FileNotFoundError("无法加载图像/模板文件，请检查路径")

# 获取模板的高、宽（模板shape为[高, 宽, 通道]，故h=shape[0], w=shape[1]）
h, w = template.shape[:2]  


# 2. 模板匹配
# 2.1 执行模板匹配（使用归一化相关系数匹配，结果更稳定）
res = cv.matchTemplate(img, template, cv.TM_CCOEFF_NORMED)  # 建议用归一化方法减少亮度影响

# 2.2 查找最佳匹配位置并绘制矩形
min_val, max_val, min_loc, max_loc = cv.minMaxLoc(res)  
# 注：当前使用的TM_CCOEFF_NORMED是相关系数匹配，最佳位置为最大值（若用TM_SQDIFF则取最小值）
top_left = max_loc  

# 计算匹配区域的右下角坐标（模板宽w、高h）
bottom_right = (top_left[0] + w, top_left[1] + h)  

# 在原图像上绘制绿色矩形标记匹配区域（BGR格式中(0,255,0)为绿色，线宽2）
cv.rectangle(img, top_left, bottom_right, (0, 255, 0), 2)  


# 3. 图像显示（Matplotlib需BGR→RGB转换，关闭坐标轴）
plt.imshow(img[:, :, ::-1])  # ::-1实现BGR到RGB的反转
plt.title('匹配结果')
plt.xticks([]), plt.yticks([])  # 隐藏坐标轴刻度
plt.show()

找到了目标区域，效果如下：

2.2 霍夫变换

霍夫变换

定义

霍夫变换常⽤来提取图像中的直线和圆等⼏何形状，如下图所示：

比如，检测直线的原理如下：👇

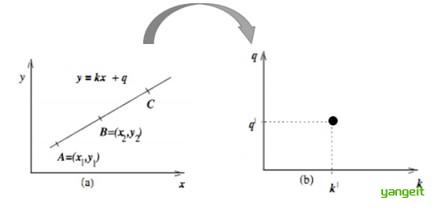
笛卡尔坐标系中的⼀条直线，对应于霍夫空间中的⼀个点。反过来，同样成⽴，霍夫空间中的⼀条线，对应于笛卡尔坐标系中
⼀个点，如下所示：

霍夫线检测的整个流程如下图所示：

2. 霍夫线检测

在OpenCV中做霍夫线检测是使⽤的API是：

lines = cv.HoughLines(image, rho, theta, threshold)


参数说明：
- image：输入图像，必须是8位的单通道二值图像，通常由Canny边缘检测算法得到；
- rho：以像素为单位的距离精度，通常取1；
- theta：以弧度为单位的角度精度，通常取1度（π/180）；
- threshold：累加器阈值参数，只有⽤于霍夫空间的交点累加值⽐这个阈值⼤的线才被检测出来，通常取阈值默认值100即可。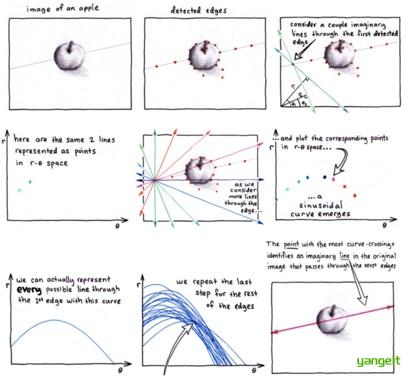

案例1：直线检测：

检测下面的直线图像：

import numpy as np
import random
import cv2 as cv
import matplotlib.pyplot as plt

# 1. 加载图片并预处理为二值边缘图
img = cv.imread('./img/rili.png')
if img is None:
    raise FileNotFoundError("无法加载图像文件，请检查路径")

# 转为灰度图 → Canny边缘检测
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
edges = cv.Canny(gray, 50, 150)  # Canny阈值：低阈值50，高阈值150（需根据实际图像调整）

# 2. 霍夫直线变换
# 参数说明：edges-边缘图；0.8-距离分辨率(ρ)；np.pi/180-角度分辨率(θ，1度)；150-累加器阈值(投票数>150才视为直线)
lines = cv.HoughLines(edges, 0.8, np.pi/180, 150)

# 3. 将检测到的直线绘制在原图上（极坐标转直角坐标）
if lines is not None:  # 避免无直线时出错
    for line in lines:
        rho, theta = line[0]  # 霍夫直线参数：rho=极径，theta=极角（极坐标表示）
        
        # 极坐标转直角坐标：直线一般式ax + by = rho
        a = np.cos(theta)
        b = np.sin(theta)
        x0 = a * rho  # 直线上任意一点(x0,y0)
        y0 = b * rho
        
        # 延长直线（取1000长度的线段，避免线段过短看不清）
        # 方向向量(-b,a)与(b,-a)垂直直线方向，用于生成线段两端点
        x1 = int(x0 + 1000 * (-b))  
        y1 = int(y0 + 1000 * (a))   
        x2 = int(x0 - 1000 * (-b))  
        y2 = int(y0 - 1000 * (a))   
        
        # 绘制绿色直线（BGR格式中(0,255,0)为绿色）
        cv.line(img, (x1, y1), (x2, y2), (0, 255, 0), 2)

# 4. 图像显示（BGR→RGB转换，调整画布大小）
plt.figure(figsize=(10, 8), dpi=100)  # 修正"1θ"→"10"
plt.imshow(img[:, :, ::-1]), plt.title('霍夫变换线检测')
plt.xticks([]), plt.yticks([])  # 隐藏坐标轴
plt.show()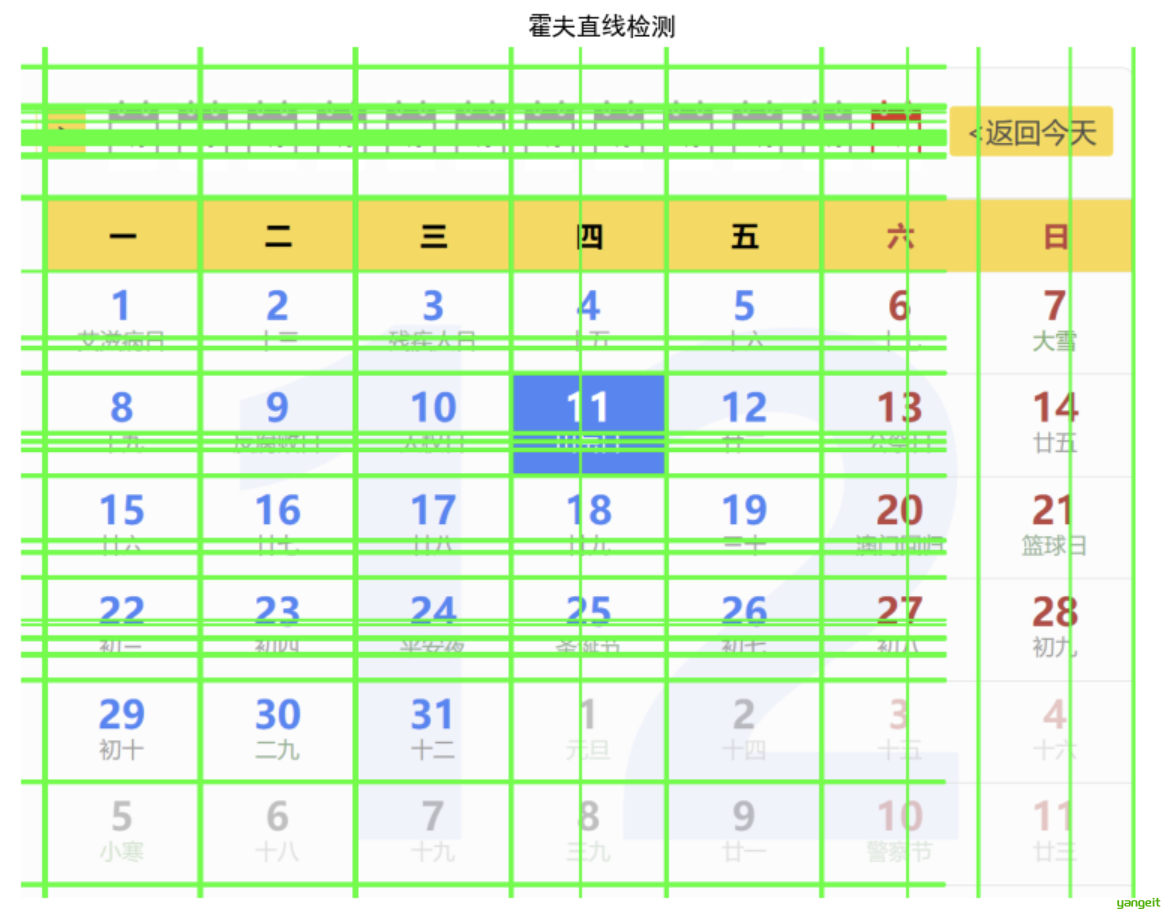

案例2：检测圆形，opencv中霍夫圆检测的API是：

circles = cv.HoughCircles(image, method, dp, minDist)


参数说明：

- image：输入图像，必须是8位的灰度图像；
- method：圆检测的方法，OpenCV中只实现了霍夫梯度法（CV_HOUGH_GRADIENT）；
- dp：累加器分辨率与图像分辨率的比值，通常取1，表示与图像的分辨率相同；
- minDist：两个圆之间的最小距离；

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

# 1. 读取图像并转换为灰度图（修正颜色转换码：BGRA→BGR）
planets = cv.imread("./img/star1.png")
if planets is None:
    raise FileNotFoundError("无法加载图像文件，请检查路径")

# 注：若原图像为4通道(BGRA)，用COLOR_BGRA2GRAY；若为3通道(BGR)，用COLOR_BGR2GRAY
# 此处假设原图像为3通道，修正为COLOR_BGR2GRAY（若为4通道需改回COLOR_BGRA2GRAY）
gray_img = cv.cvtColor(planets, cv.COLOR_BGR2GRAY)  # 修正"gay_img"→"gray_img"（拼写错误）

# 2. 中值模糊去噪（修正"2θθ"→"200"：中值滤波核大小需为正奇数，7是合理的）
img_blur = cv.medianBlur(gray_img, 7)  # 核大小7×7，有效去除椒盐噪声

# 3. 霍夫圆检测
# 参数说明：
# - cv.HOUGH_GRADIENT：梯度法（最常用）；
# - 1：累加器分辨率与原图的比例（1表示相同）；
# - 100：两个圆之间的最小距离（避免重复检测相邻圆）；
# - param1：Canny边缘检测的高阈值（低阈值为其一半，即50）；
# - param2：累加器阈值（越小检测越多圆，需根据图像调整）
circles = cv.HoughCircles(
    img_blur, 
    cv.HOUGH_GRADIENT, 
    1, 
    100, 
    param1=80, 
    param2=55, 
    minRadius=0,   # 最小圆半径（可选，默认0）
    maxRadius=0    # 最大圆半径（可选，默认0表示无限制）
)

# 4. 将检测结果绘制在图像上（需先判断是否有检测到圆）
if circles is not None:
    # 转换为整数坐标（霍夫圆检测返回浮点数，需取整）
    circles = np.uint16(np.around(circles))  
    
    for i in circles[0, :]:  # 遍历每个圆的参数（circles shape为[1, N, 3]，N为圆的数量）
        center_x, center_y, radius = i[0], i[1], i[2]  # i[0]=圆心x，i[1]=圆心y，i[2]=半径
        
        # 绘制圆形轮廓（绿色，线宽2）
        cv.circle(planets, (center_x, center_y), radius, (0, 255, 0), 2)  
        # 绘制圆心（红色，半径2，线宽3）
        cv.circle(planets, (center_x, center_y), 2, (0, 0, 255), 3)  

# 5. 图像显示（修正"1θ"→"10"、"::–1"→"::-1"）
plt.figure(figsize=(10, 8), dpi=100)  # 设置画布大小（宽10英寸，高8英寸）
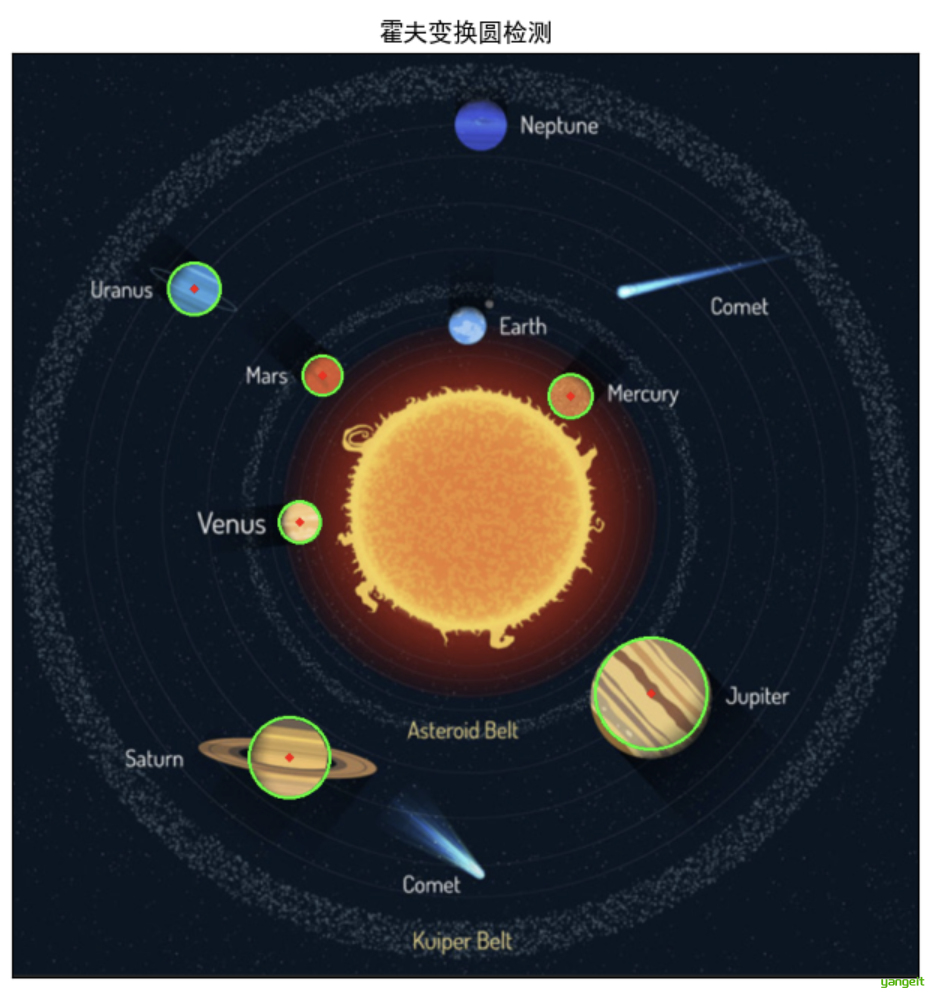
plt.imshow(planets[:, :, ::-1]), plt.title('霍夫变换圆检测')  # BGR→RGB转换
plt.xticks([]), plt.yticks([])  # 隐藏坐标轴
plt.show()