OpenCV入门案例2

yange大约 17 分钟

1. 几何变换

前言

定义

学习目标

掌握图像的缩放，平移，旋转等
了解数字图像的仿射变换和透射变换

1. 图像的缩放

缩放是对图像的⼤⼩进⾏调整，即使图像放⼤或缩⼩。

缩放函数：

cv2.resize(src, dsize, fx=0, fy=0, interpolation=INTER_LINEAR) → dst

参数说明：

src：源图像
dsize：输出图像的⼤⼩。
fx：沿水平轴的缩放系数
fy：沿垂直轴的缩放系数
interpolation：插值⽅法。默认情况下是INTER_LINEAR。

示例：

import cv2
import numpy as np

# 读取图像
img = cv2.imread('dog.jpg')

# 缩放图像
resized_img = cv2.resize(img, (0, 0), fx=0.5, fy=0.5) # 第一个参数是图像，第二个参数是输出图像的尺寸，fx和fy是缩放系数

# 显示图像
cv2.imshow('Original Image', img)
cv2.imshow('Resized Image', resized_img)
cv2.waitKey(0)
cv2.destroyAllWindows()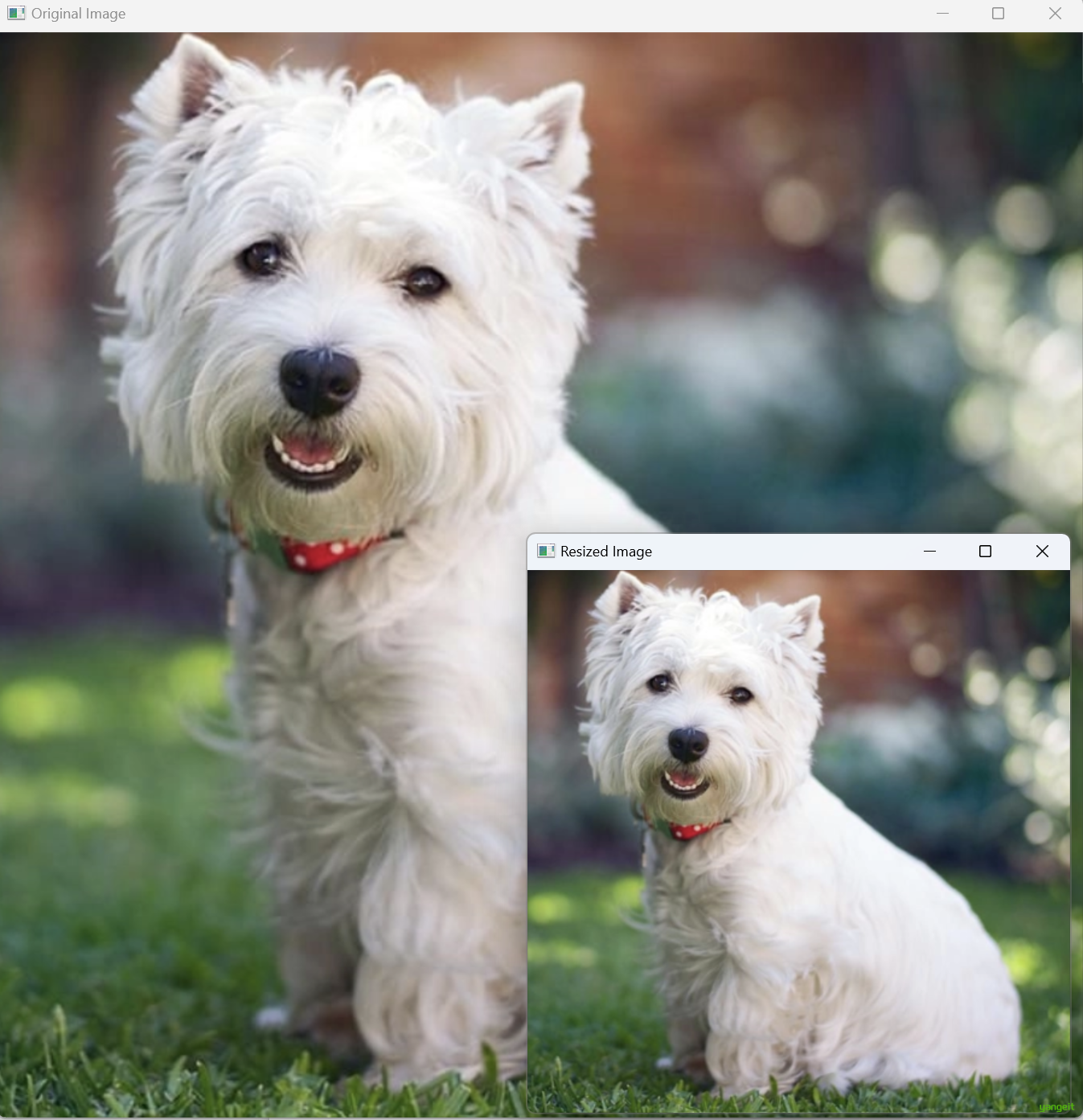

2. 图像的平移

图像平移将图像按照指定⽅向和距离，移动到相应的位置。

平移函数：

cv2.warpAffine(src, M, dsize, flags=INTER_LINEAR, borderMode=BORDER_CONSTANT, borderValue=None) → dst

参数说明：

src：源图像
M：2x3的变换矩阵
dsize：输出图像的⼤⼩
flags：插值⽅法。默认情况下是INTER_LINEAR。
borderMode：边界模式。默认情况下是BORDER_CONSTANT。

示例：

import cv2
import numpy as np

# 读取图像
img = cv2.imread('dog.jpg')

# 定义平移矩阵
M = np.float32([[1, 0, 100], [0, 1, 50]]) # 向右平移100像素，向下平移50像素

# 平移图像
translated_img = cv2.warpAffine(img, M, (img.shape[1], img.shape[0]))

# 显示图像
cv2.imshow('Original Image', img)
cv2.imshow('Translated Image', translated_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

3. 图像的旋转

图像旋转是指图像按照某个位置转动⼀定⻆度的过程，旋转中图像仍保持这原始尺寸图像旋转后图像的⽔平对称轴垂直对称轴及中⼼坐标原点都可能会发⽣变换，因此需要对图像旋转中的坐标进⾏相应转换。

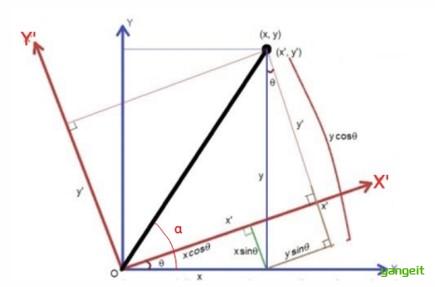
函数：

cv2.getRotationMatrix2D(center, angle, scale) → retval

参数说明：

center：旋转中心
angle：旋转⻆度
scale：缩放⽐例

示例：

import cv2
import numpy as np

# 读取图像
img = cv2.imread('./img/dog1.png')

# 定义旋转矩阵
M = cv2.getRotationMatrix2D((img.shape[1]//2, img.shape[0]//2), 45, 1) # 旋转45度

# 旋转图像
rotated_img = cv2.warpAffine(img, M, (img.shape[1], img.shape[0]))

# 显示图像
cv2.imshow('Original Image', img)
cv2.imshow('Rotated Image', rotated_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

4. 图像的仿射变换

什么是图像的仿射变换？

如下图所示，图1中的点1, 2 和 3 与图二中三个点一一映射, 仍然形成三⻆形, 但形状已经⼤⼤改变，通过这样两组三点（感兴趣点）求出仿射变换，接下来我们就能把仿射变换应⽤到图像中所有的点中，就完成了图像的仿射变换。

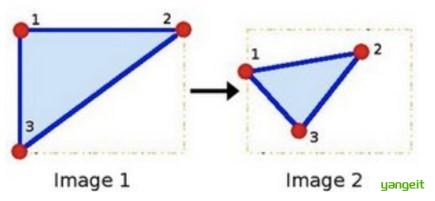
类似把纸盒子压扁，然后再放回去，纸盒子就变形了，但纸盒子内部的纸张还是原来的样子，这就是仿射变换。


import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt

# 1. 图像读取（请确保./image/image2.jpg存在）
img = cv2.imread('./img/dog1.png')

# 2. 仿射变换
rows, cols = img.shape[:2]

# 2.1 创建变换矩阵（修正原代码中的θ为0）
pts1 = np.float32([[50, 50], [200, 50], [50, 200]])  # 原始三角形三个点
pts2 = np.float32([[100, 100], [200, 50], [100, 250]])  # 变换后目标位置
M = cv.getAffineTransform(pts1, pts2)  # 计算2x3仿射变换矩阵

# 2.2 执行仿射变换
dst = cv.warpAffine(img, M, (cols, rows))  # 输出图像尺寸保持不变

# 3. 图像显示（BGR→RGB转换）
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 8), dpi=100)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:, :, ::-1])
axes[1].set_title("仿射变换结果")

plt.tight_layout()
plt.show()

2. 形态学操作

前言

定义

学习目标 👇

理解图像的邻域，连通性
了解不同的形态学操作：腐蚀，膨胀，开闭运算，礼帽和⿊帽等，及其不同操作之间的关系

1.连通性

在图像中，最⼩的单位是像素，每个像素周围有8个邻接像素，常⻅的邻接关系有3种：4邻接、8邻接和D邻接。分别如下图所示：

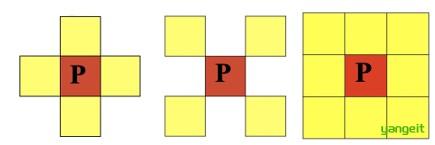
4邻接：像素 p(x,y)的 4 邻域：(x+1,y)、(x−1,y)、(x,y+1)、(x,y−1)，用P4(p)表示像素 p的 4 邻接
D邻接：像素 p(x,y)的 D 邻域：对角上的点 (x+1,y+1)、(x+1,y−1)、(x−1,y+1)、(x−1,y−1),用 PD(p)表示像素 p的 D 邻域
8邻接:像素 p(x,y)的 8 邻域：4 邻域的点＋ D 邻域的点,用 P 8(p)表示像素 p的 8 邻域

连通性是描述区域和边界的重要概念，两个像素连通的两个必要条件是：

两个像素的位置是否相邻
两个像素的灰度值是否满足特定的相似性准则（或者是否相等根据连通性的定义，有4联通、8联通和m联通三种。

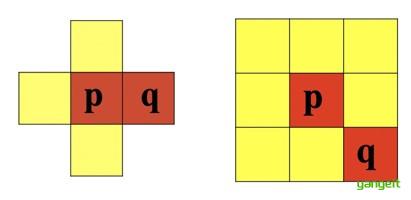
4联通：对于具有值V 的像素p和q，如果q在集合P4(p)中，则称这两个像素是4连通
8联通：对于具有值V 的像素p和q，如果q在集合P8(p)中，则称这两个像素是8连通。

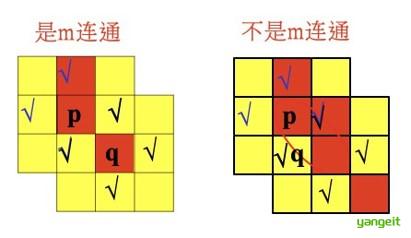
对于具有值V的像素p和q，如果:

q在集合P4(p)中，或
q在集合PD(p)中，并且P4(p)与P4(q)的交集为空（没有值V 的像素）则称这两个像素是m连通的，即4连通和D连通的混合连通。

2. 形态学操作

形态学转换是基于图像形状的⼀些简单操作。它通常在⼆进制图像上执⾏。腐蚀和膨胀是两个基本的形态学运算符。然后它的变体形式如开运算，闭运算。

1. 腐蚀

腐蚀操作时取每一个位置的矩形邻域内值的最小值作为该位置的输出灰度值。这里的邻域可以是矩形结构，也可以是椭圆形结构、十字交叉形结构等，这个结构被定义为结构元，实际上就是个01二值矩阵。

举个例子：

给定一个矩阵，也就是我们要做处理的图像,以及一个十字交叉结构元

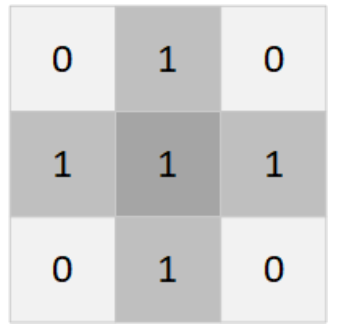
在对(1,2)点出的灰度做处理时，也就是对21这个点做处理时，要在其十字形邻域内找最小值，赋值给
点。示意图如下:

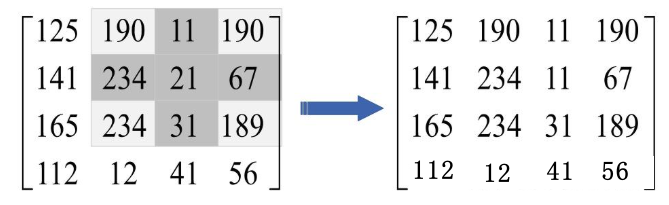
从图中也可以很容易的看出，腐蚀操作将灰度值降低了,变成了11，也就是说腐蚀后的输出图像总体亮度比原图有所降低，图像中比较亮的区域面积会变小，比较暗的区域面积增大。

粗略的说，腐蚀可以使目标区域范围“变小”，其实质造成图像的边界收缩，

记忆策略：腐蚀，可以联想到浓硫酸腐蚀，浓硫酸会让木头、纸腐蚀，最后变黑。

应用场景：

腐蚀能将连接的对象分开

腐蚀能去除喷溅突出

腐蚀会缩小图像

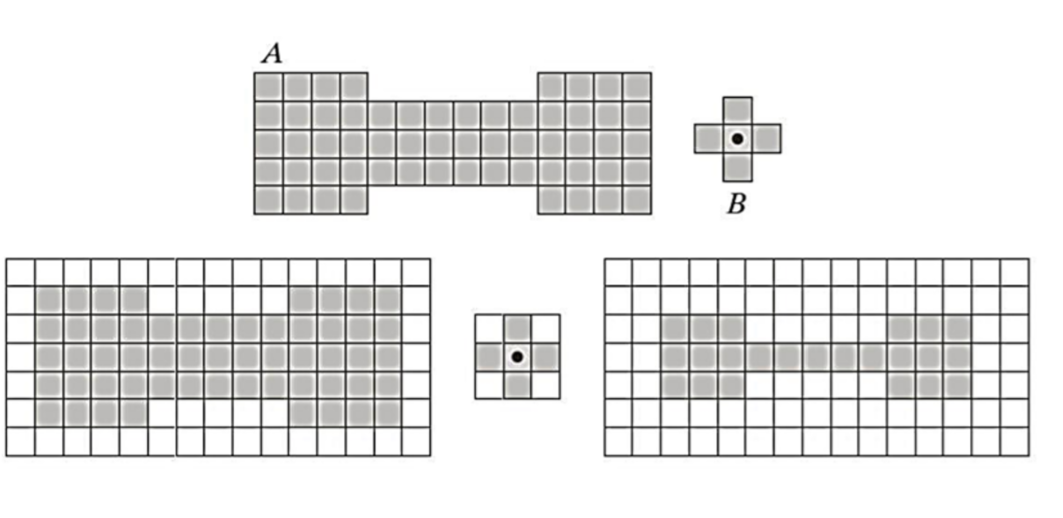
2. 膨胀

膨胀操作时取每一个位置的矩形邻域内值的最大值作为该位置的输出灰度值。

膨胀相当于是腐蚀反向操作，图像中较亮的物体尺寸会变大，较暗的物体尺寸会减小。还是相同的例子，在21的十字邻域内找最大值，最大值为234，将234赋值到这个位置。

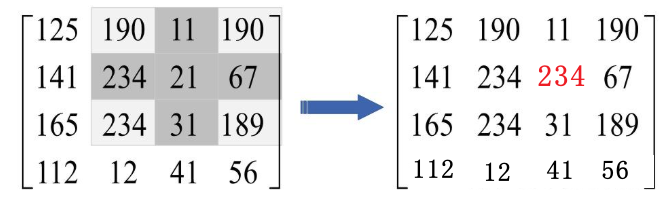
记忆策略：玉米经过加热后越来越大，也越来越白

应用场景：

膨胀可修复图像断裂

膨胀可修复侵入突出

膨胀会放大图像

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负

img = cv2.imread('./img/wirebond-mask.tif', 0) # 读取骰(tou)子灰度图
# 得到一个3x3的十字交叉结构元，实际就是numpy矩阵
kernel = cv2.getStructuringElement(cv2.MORPH_CROSS,(3,3)) 
erode_res = cv2.erode(img, kernel)  # 腐蚀结果
dilate_res = cv2.dilate(img, kernel)  # 膨胀结果

plt.subplot(1,3,1)
plt.imshow(erode_res, cmap=plt.cm.gray)
plt.title("腐蚀效果")

plt.subplot(1,3,2)
plt.imshow(img, cmap=plt.cm.gray)
plt.title("原图")

plt.subplot(1,3,3)
plt.imshow(dilate_res, cmap=plt.cm.gray)
plt.title("膨胀效果")
plt.show()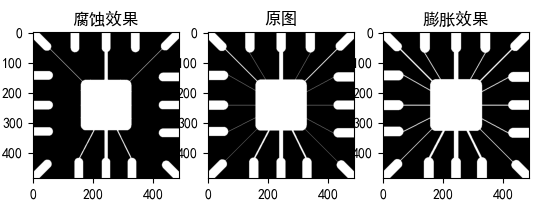

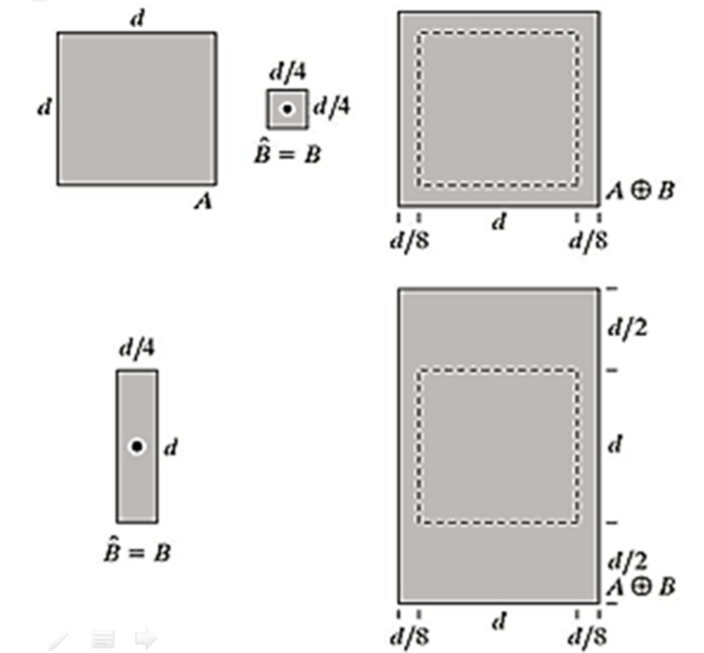
3. 开运算

膨胀使图像变大，腐蚀使图像变小，为保持图像大小，膨胀与腐蚀通常成对出现。

开运算是先腐蚀后膨胀，可以消除亮度较高的细小区域,让轮廓变得光滑，而且不会明显改变其他物体区域的面积。

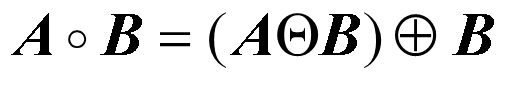
记忆策略：要打开一个东西, 就先腐蚀, 腐蚀了才能打开

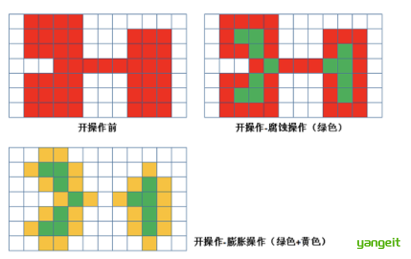
开运算的几何解释：类似于B在一个轮廓内部滚动，开运算会去除外尖角

4.闭运算

闭运算与开运算相反，先膨胀后腐蚀。可以消除细小黑色空洞，也不会明显改变其他物体区域面积。

记忆策略：欲使其自闭，必先让其膨胀

案例代码 👇

1 案例2 ✏️

import numpy as np
import cv2
from matplotlib import pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负

img = cv2.imread(r'./img/morphology.png',0)
# img = cv2.imread(r'./img/fingerprint.png',0) # 指纹图
_, img_binary = cv2.threshold(img, 128, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
kernelSize=33  #换成指纹头，要修改核大小哦，建议从1开始试
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(kernelSize,kernelSize))
img_erode = cv2.erode(img_binary,kernel,iterations = 1)
img_dilate = cv2.dilate(img_binary, kernel, iterations=1)
img_open = cv2.morphologyEx(img_binary, cv2.MORPH_OPEN, kernel)
img_close = cv2.morphologyEx(img_binary, cv2.MORPH_CLOSE, kernel)
plt.figure(figsize=(12,4))
plt.subplot(151)
plt.axis("off")
plt.imshow(img_binary,cmap="gray")
plt.title("原图")

plt.subplot(1,5,2)
plt.axis("off")
plt.imshow(img_erode,cmap="gray")
plt.title("腐蚀")

plt.subplot(1,5,3)
plt.axis("off")
plt.imshow(img_dilate,cmap="gray")
plt.title("膨胀")
plt.subplot(1,5,4)
plt.axis("off")
plt.imshow(img_open,cmap="gray")
plt.title("开运算")
plt.subplot(1,5,5)
plt.axis("off")
plt.imshow(img_close,cmap="gray")
plt.title("闭运算")
plt.show()

3. 图像平滑

前言

定义

学习目标：👇

了解图像中的噪声类型
了解平均滤波，⾼斯滤波，中值滤波等的内容
能够使⽤滤波器对图像进⾏处理

1. 图像噪声

由于图像采集、处理、传输等过程不可避免的会受到噪声的污染，妨碍⼈们对图像理解及分析处理。常⻅的图像噪声有⾼斯噪声、椒盐噪声等

1.1 椒盐噪声

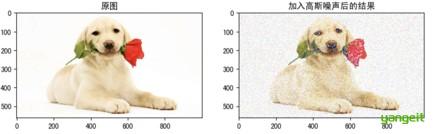
椒盐噪声也称为脉冲噪声，是图像中经常⻅到的⼀种噪声，它是⼀种随机出现的⽩点或者⿊点，可能是亮的区域有⿊⾊像素或是在暗的区域有⽩⾊像素（或是两者皆有）。椒盐噪声的成因可能是影像讯号受到突如其来的强烈⼲扰⽽产⽣、类⽐数位转换器或位元传输错误等。例如失效的感应器导致像素值为最⼩值，饱和的感应器导致像素值为最⼤值。

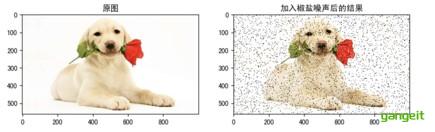
1.2 高斯噪声

⾼斯噪声是指噪声密度函数服从⾼斯分布的⼀类噪声。由于⾼斯噪声在空间和频域中数学上的易处理性，这种噪声(也称为正态噪声)模型经常被⽤于实践中,分布如下：

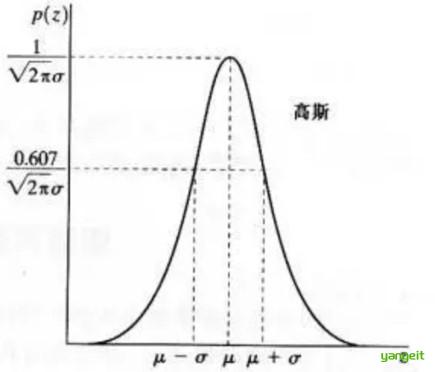
2. 平滑滤波：给图像“磨皮降噪”

1. 适用场景

解决照片中的斑点噪点（如夜景照片的颗粒感、老照片的杂点），让画面更柔和。

2. 常见类型

均值滤波：最基础的平滑方法。计算窗口内所有像素的灰度平均值，用平均值替换中心像素。
- 类比：班级里求平均分，用平均分代表中心像素的“水平”，能快速弱化噪点，但会让画面轻微模糊。
高斯滤波：对均值滤波的改进，用高斯函数对窗口内像素的灰度值进行加权平均，用加权平均值替换中心像素。
- 类比：班级里用高斯函数对每个同学的分数进行加权平均，能更精准地代表班级水平，但计算量更大。

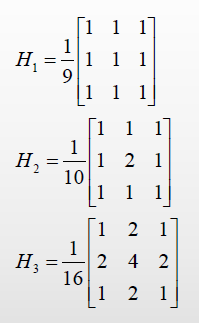
阈值邻域平滑滤波：就是将原有像素点的灰度值和均值滤波后的灰度值进行比较，如果灰度值之差小于一个阈值，认为当前像素不是噪点，否则认为是噪点，用均值滤波后的灰度值替换当前像素的灰度值。
- 类比：班级里，如果一个同学的分数和班级平均分之差小于一个阈值，认为该同学不是“保守学生”，否则认为该同学是“保守学生”，“保守学生”的分数用班级平均分替换。
中值滤波：对窗口内的像素灰度值排序，取中间值替换中心像素。
- 类比：评选班级中等水平的同学，能精准去除“椒盐噪点”（画面中突兀的黑白小点），且比均值滤波更能保留图像细节。

3. 生活案例

把有很多雀斑的照片用中值滤波处理，雀斑（噪点）会消失，同时人脸的轮廓、五官细节不会明显模糊。

高斯滤波代码：👇

import cv2
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负

img = cv2.imread(r'./img/lena.jpg')
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
img_gaussian = cv2.GaussianBlur(img, (5, 5), 0)
plt.subplot(121)
plt.imshow(img)
plt.title("原图")
plt.subplot(122)
plt.imshow(img_gaussian)
plt.title("高斯滤波")
plt.show()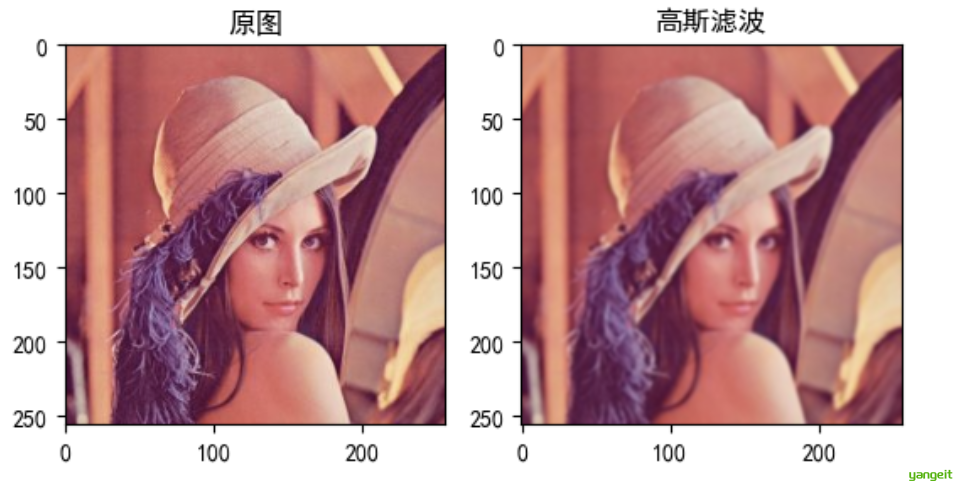

4. 直方图

前言

定义

直方图定义

对于一幅灰度图像（像素值范围通常是0-255，0为纯黑，255为纯白），其灰度直方图是一个统计图表，横轴表示灰度级（0~255），纵轴表示该灰度级在图像中出现的像素数量（或频率）。

图像直方图
表示数字图像中亮度分布的直方图，横坐标是亮度值，纵坐标是该亮度值的像素个数；左侧为较暗区域，右侧为较亮区域。
较暗图片：直方图中数据多集中于左侧和中间部分
整体明亮、只有少量阴影的图片：直方图数据分布相反（集中在右侧）

2. 直方图的直观意义
直方图的形状反映了图像中像素灰度的分布规律：

双峰直方图：图像中有明显的两类像素（如前景和背景），直方图会出现两个峰值（分别对应两类像素的灰度集中区域），两峰之间的谷底通常可以作为分割阈值。

单峰直方图：图像中像素灰度分布均匀（如渐变图像），难以直接通过阈值分割。

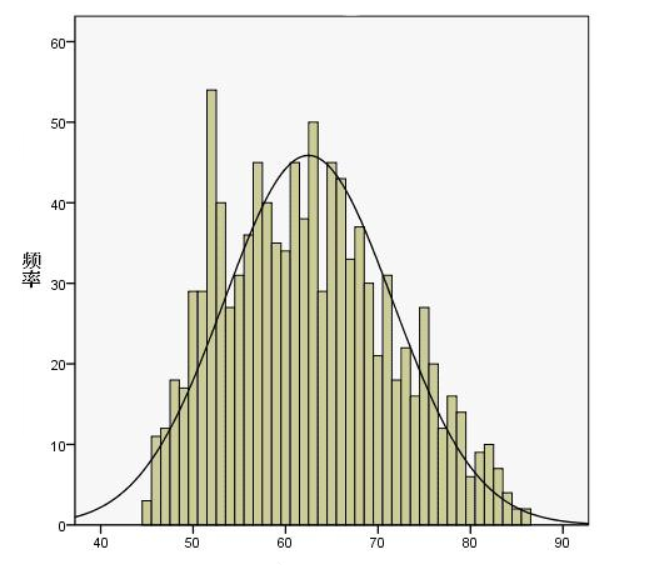
3. 绘制图像的直方图

import cv2
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负

img = cv2.imread(r'./img/fingerprint.png', 0) # 读取灰度图像
# 显示原图
plt.subplot(121)
plt.imshow(img, cmap='gray')
plt.title("原图")
plt.subplot(122)


# 2.统计直方图
hist = cv2.calcHist([img], [0], None, [256], [0, 256]) # 参数说明：[img]表示输入图像，[0]表示通道索引，None表示不使用掩膜，[256]表示直方图大小，[0,256]表示像素值范围
# 3.绘制直方图
plt.plot(hist)
plt.show()

掩膜是用选定的图像、图形或物体，对要处理的图像进⾏遮挡，来控制图像处理的区域。

5. 直方图均衡化

前言

定义

想象一下，如果一幅图像中的大多数像素点的像素值都集中在某一个小的灰度值范围之内会怎样呢？如果一幅图像整体很亮，那所有的像素值的取值个数应该都会很高。所以应该把它的直方图做一个横向拉伸（如下图），就可以扩大图像像素值的分布范围，提高图像的对比度，这就是直方图均衡化要做的事情。

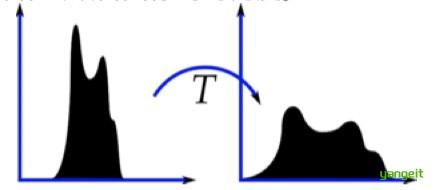
直方图均衡化是把原始图像的灰度直方图从比较集中的某个灰度区间变成在更广泛灰度范围内的分布。直方图均衡化就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同。

这种方法提高图像整体的对比度，特别是当有用数据的像素值分布比较接近时，在X光图像中使用广泛，可以提高骨架结构的显示，另外在曝光过度或不足的图像中可以更好地突出细节。


import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

# 1. 以灰度图方式读入
img = cv.imread('./img/cat.png', 0)

# 2. 均衡化处理
dst = cv.equalizeHist(img)

# 3. 结果展示：原图与均衡化图
fig1, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 4), dpi=100)
axes[0].imshow(img, cmap=plt.cm.gray)
axes[0].set_title("原图")
axes[0].axis('off')

axes[1].imshow(dst, cmap=plt.cm.gray)
axes[1].set_title("均衡化后结果")
axes[1].axis('off')

plt.tight_layout()

# 4. 直方图显示：原图直方图与均衡化后直方图
fig2, axes_hist = plt.subplots(nrows=1, ncols=2, figsize=(10, 4), dpi=100)

# 计算直方图
hist1 = cv.calcHist([img], [0], None, [256], [0, 256])
hist2 = cv.calcHist([dst], [0], None, [256], [0, 256])

# 绘制原图直方图
axes_hist[0].plot(hist1, color='black')
axes_hist[0].set_title("原图直方图")
axes_hist[0].set_xlim([0, 256])
axes_hist[0].grid(True, linestyle='--', alpha=0.5)

# 绘制均衡化后直方图
axes_hist[1].plot(hist2, color='black')
axes_hist[1].set_title("均衡化后直方图")
axes_hist[1].set_xlim([0, 256])
axes_hist[1].grid(True, linestyle='--', alpha=0.5)

plt.tight_layout()
plt.show()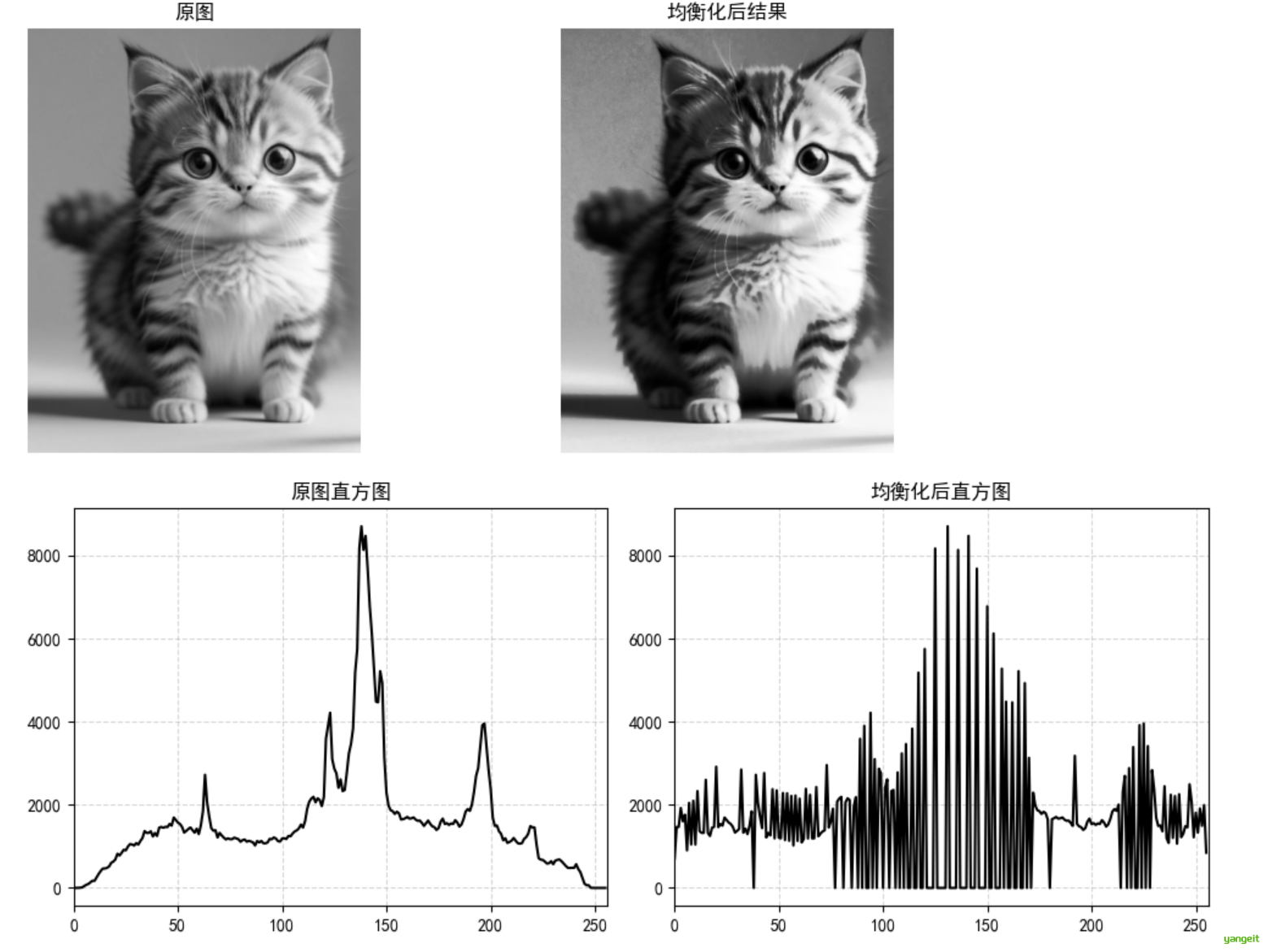

6. 自适应直方图均衡化

前言

定义

上述的直方图均衡化，我们考虑的是图像的全局对比度。确实在进行完直方图均衡化之后，图片背景的对比度被改变了，在猫腿这里太暗，我们丢失了很多信息，所以在许多情况下，这样做的效果并不好。如下图所示，对比下两幅图像中雕像的画面，由于太亮我们丢失了很多信息。

为了解决这个问题，需要使用自适应的直方图均衡化。此时，整幅图像会被分成很多小块，这些小块被称为“tiles”（在 OpenCV 中 tiles 的大小默认是 8×8），然后再对每一个小块分别进行直方图均衡化。所以在每一个区域中，直方图会集中在某一个小区域中。如果有噪声的话，噪声会被放大。为了避免这种情况的出现要使用对比度限制。对于每个小块来说，如果直方图中的 bin 超过对比度的上限的话，就把其中的像素点均匀分散到其他 bins 中，然后再进行直方图均衡化。最后，为了去除每一个小块之间的边界，再使用双线性插值，对每一小块进行拼接。


import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

# 1. 以灰度图形式读取图像
img = cv.imread('./img/cat.png', 0)

# 2. 创建一个自适应均衡化的对象，并应用于图像
clahe = cv.createCLAHE(clipLimit=2.0, tileGridSize=(6, 6)) # 参数说明：clipLimit：对比度限制，tileGridSize：tiles的大小
cl1 = clahe.apply(img)

# 3. 图像展示
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 8), dpi=100)
axes[0].imshow(img, cmap=plt.cm.gray)
axes[0].set_title("原图")
axes[0].axis('off')

axes[1].imshow(cl1, cmap=plt.cm.gray)
axes[1].set_title("自适应均衡化后的结果")
axes[1].axis('off')

plt.tight_layout()
plt.show()