第九章图像描述和特征提取

yange大约 22 分钟数字图像处理数字图像处理

1. 灰度图像的描述

前言

定义

众所周知，计算机不认识图像，只认识数字，为了使计算机能够识别图像，就需要将图像转换为数字，这个过程称为图像处理。

在前序章节中，我们系统学习了图像的基础处理技术（如滤波、增强、边缘检测等），这些操作的核心目标是改善图像质量或突出特定信息。但若要让计算机真正“理解”图像内容（例如判断图中是猫还是狗、识别工业零件是否缺陷），仅靠处理后的图像本身是不够的——我们需要从图像中提取能反映其本质属性的“特征”，并通过结构化的描述将这些特征转化为可计算、可比较的信息单元。

本章聚焦图像描述与特征提取，这是连接“图像处理”与“图像分析/理解”的关键桥梁。其中，灰度图像作为最基础的图像类型（单通道，仅包含亮度信息），其描述方法是后续彩色图像、纹理图像等复杂场景特征提取的基石。我们将首先从灰度图像的全局特性出发，学习三类典型的描述特征：幅度特征、变换系数特征和直方图特征。

灰度图像的描述旨在通过数学量或统计量，刻画图像整体的亮度分布、对比度、能量聚集等宏观特性。这些特征不依赖像素级细节（如边缘位置），而是从整体层面反映图像的“宏观印象”，常用于图像分类、质量评估、检索等任务的前期分析。

1.幅度特征：图像亮度的直观量化

核心思想：直接基于图像像素的灰度值（即亮度幅度）计算全局统计量，反映图像的整体明暗程度与变化范围。

典型指标：

平均灰度（均值）：所有像素灰度值的算术平均，描述图像的整体亮度水平。公式为：

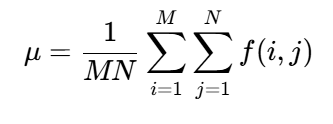
其中M×N为图像尺寸，f(i,j)为坐标(i,j)处的灰度值。

应用场景：低均值可能对应暗背景图像（如夜景），高均值可能对应明亮场景（如雪地）。

灰度方差/标准差：衡量像素灰度值相对于均值的离散程度，反映图像的对比度（明暗差异大小）
特点：方差越大，说明图像中同时存在较亮和较暗的像素（对比度高，如强光下的物体轮廓）；方差越小，图像整体偏灰（对比度低，如雾天场景）。
最大/最小灰度值：直接给出图像中最亮和最暗的像素亮度，可用于检测极端亮度区域（如过曝或欠曝部分）。

2.变换系数特征：

核心思想：通过傅里叶变换、小波变换等频域转换方法，将图像从空间域（像素矩阵）转换到频域（不同频率成分的叠加），提取各频率分量的系数特征，反映图像的“全局结构模式”。

典型方法与特征：

傅里叶变换系数：将图像转换到频域后，得到复数形式的频谱（包含幅度谱和相位谱）。其中：
- 低频系数（靠近频谱中心）：对应图像中缓慢变化的成分（如大面积均匀区域、整体背景亮度）。
- 高频系数（远离频谱中心）：对应图像中快速变化的成分（如边缘、噪声、细节纹理）。
  常用特征：低频系数的总能量（反映图像主体结构的稳定性）、高频系数的能量占比（反映细节丰富程度）。例如，医学X光片中，若高频能量占比高，可能意味着骨骼边缘清晰；若低频能量主导，则可能图像整体模糊。

3. 直方图特征：灰度分布的概率描述

核心思想：通过统计图像中每个灰度级（通常为0~255）出现的像素数量或概率，构建灰度直方图，进而提取能反映亮度分布模式的统计特征。
直方图定义：设图像灰度级范围为 $L$ 级（如8-bit图像 $L=256$ ），第 $k$ 级灰度值（ $k=0,1,...,L-1$ ）的像素数为 $n_k$ ，则归一化直方图（概率分布）为：

典型直方图特征：

直方图均值：与空间域的平均灰度一致，但通过概率加权计算，更强调灰度级的分布贡献。
直方图方差：同样反映对比度，但基于概率分布统计，对全局亮度变化的敏感性更高。
直方图熵：衡量灰度分布的“混乱程度”（信息量丰富度）。
- 解释：当图像灰度集中在少数级别（如纯黑或纯白背景）时，熵值低（信息单一）；当灰度均匀分布（如噪声图像）时，熵值接近最大（信息丰富）。
直方图偏斜度与峰态：进一步描述灰度分布的不对称性（偏斜度）和尖锐程度（峰态），辅助判断图像是否存在明显的亮/暗偏向（如逆光拍摄的暗部主导图像）。

二阶直方图特征：通常说的是灰度共生矩阵GLCM，统计图像中任意两个灰度级之间（特定灰度值的像素对）的联合概率分布，反映灰度级之间的相互关系。例如，若图像中存在明显的边缘结构，则二阶直方图会呈现明显的“峰”，对应于边缘两侧灰度级的联合概率。

2. 边界描述

前言

定义

边界描述的核心挑战在于：如何用简洁且具有区分性的方式表示一条可能不规则、噪声敏感的曲线？

本节将介绍两类经典方法——链码描述（基于边界像素的连接方向编码）与傅里叶描述（基于边界的频域全局建模），它们分别从“局部连接路径”和“整体形状频谱”的视角，为边界提供了高效且鲁棒的描述方案。

1. 链码描述：基于方向编码的边界路径追踪

在数字图像中，边界是由一系列离散的像素点组成的，其最简单的表示方法是由美国学者弗里曼Freeman提出的链码方法。

链码实质上是一串指向符的序列，有4向链码、8向链码等。

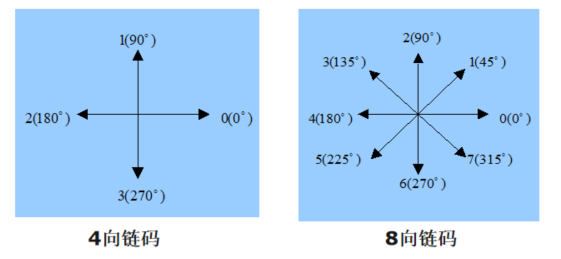
4方向链码 ：规定像素的4个邻接方向（上、下、左、右），分别用数字0、1、2、3编码（例如：向右为0，向上为1，向左为2，向下为3）。
8方向链码 （更常用）：扩展为8个邻接方向（包括对角线），用数字0~7编码（例如：正右为0，右上为1，正上为2，...，左下为7）。

逆时针数

具体操作时 ，从边界上的某个起始点（通常通过特定算法选择，如最左上角的边界点）开始，依次记录每个边界像素到下一个像素的移动方向数字，最终形成一串链码序列（例如：[0, 2, 5, 7, 3]表示“右→左上→右下→左下→左”的路径）。

结合案例理解：

案例a：

链码表示就是从某一起点开始沿曲线观察每一段的走向，并用相应的指向符来表示，结果形成一个数列。

结合上面的8向链码

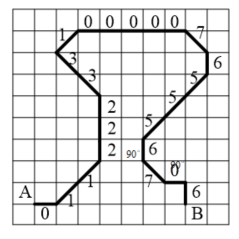
图a曲线的8链码为：01122233100000765556706

当图像进行90度旋转时，差分链码不变，但指向符会发生变化。

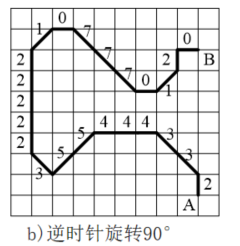
图b曲线的链码为：23344455322222107770120

差分链码：用相邻两个指向符按反方向相减，并对结果作模8运算
链码差分是关于旋转不变的边界描述方法，区域的一些其它性质，如面积和角点，可以由链码直接得

图a的差分链码为：1010010670000777001116
图b的差分链码为：1010010670000777001116

计算过程：(3-2) = 1，(3-3) = 0，(4-3) = 1，(4-4) = 0，···，(0-2) = -2 → 6

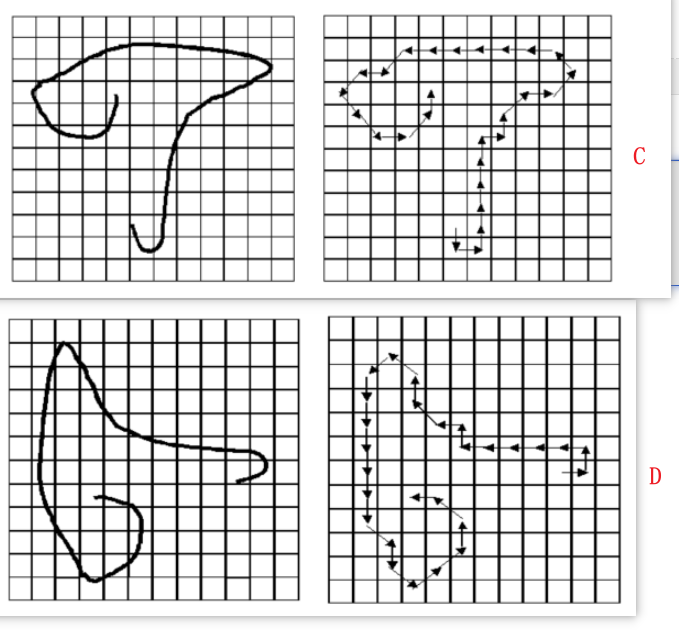
图C曲线的链码是： 602222202101344444454577012
图C其差分链码是： 22000062771210000017120111
图D曲线的链码是： 024444424323566666676711234
图D其差分链码是： 22000062771210000017120111

链码的作用：

轮廓的紧凑表示（数据压缩）
形状特征提取的基础
形状匹配与识别（核心应用）
使用差分链码进行图像数据库检索（CBIR）

缺点：

对噪声敏感：轮廓上的微小噪声会产生非常复杂的链码
尺度变化：链码本身不具有尺度不变性，需要先对轮廓进行归一化缩放
依赖于轮廓提取的质量：轮廓必须连续且单像素宽，预处理步骤至关重要

2. 傅里叶描述：基于边界的全局频谱建模

傅里叶描述通过将形状的边界表示为复数序列，然后对其进行傅里叶变换，从而得到一系列傅里叶系数，这些系数可以用来描述形状的特征.

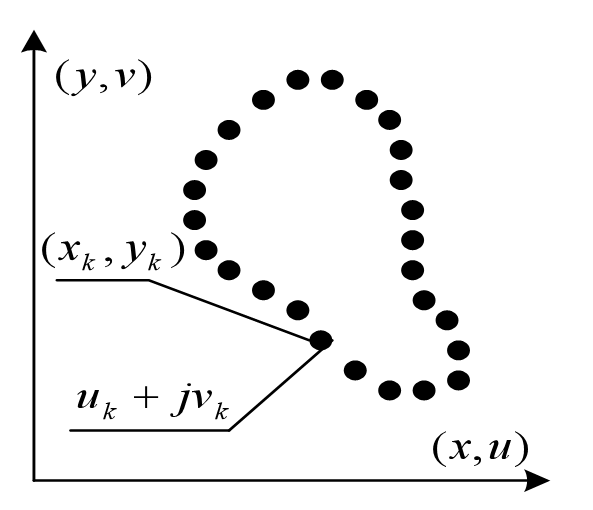
形状边界的离散点表示
首先，我们需要将目标形状的边界表示为一系列离散的点。在上图中，这些离散点可以看作是形状边界上的采样点，例如图中的黑色圆点。假设这些点的坐标为 (xk,yk)，其中 k=0,1,2,…,N−1，N是采样点的数量。

2. 复数表示

为了便于进行傅里叶变换，我们通常将二维的坐标(xk,yk)，转换为复数形式。具体来说，我们可以将每个点的坐标表示为复数的实部和虚部：

S(k)=u(k)+jv(k), k=0,1,2,…,N−1

其中，u(k)和v(k)分别是坐标的实部和虚部，j平方=-1。这样，形状的边界就可以表示为一个复数序列 S=(S(0),S(1),S(2),…,S(N−1))。

复数序列做傅里叶变换

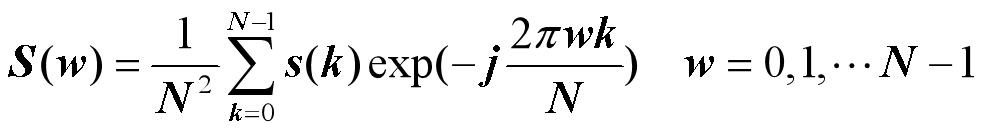
S(w)被称为傅里叶描述子

对S(w)做傅里叶反变换，只取S(w)模值最大的p个系数即可得到 s(k)的近似

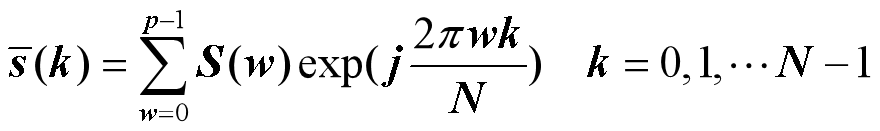
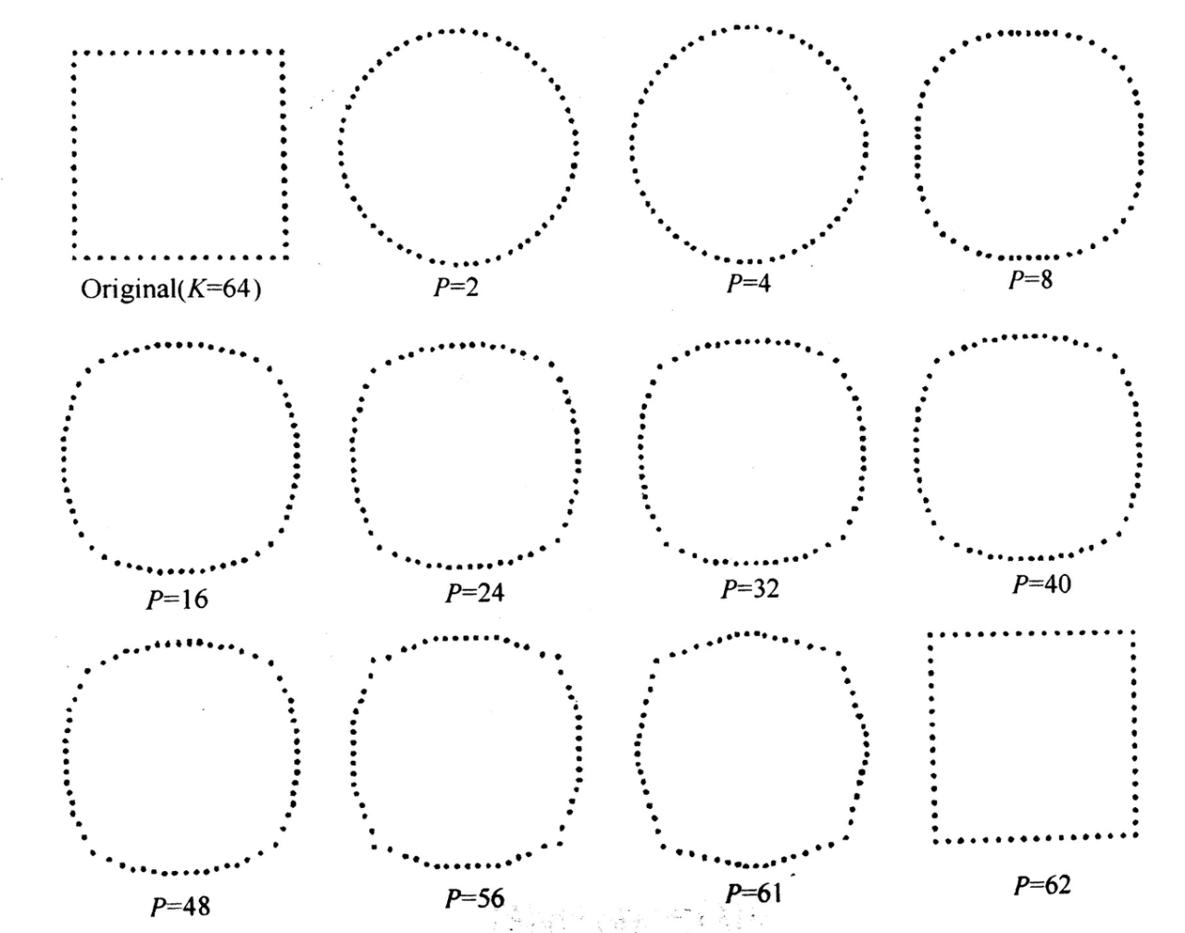
核心思想：将边界看作平面中的一条闭合曲线（由一系列边界点的坐标序列构成），通过将该坐标序列转换到频域（利用傅里叶变换），提取其不同频率成分的系数作为描述特征

低频系数反映边界的整体形状（如大致轮廓的弯曲趋势）
高频系数捕捉边界的局部细节（如小的凸起或凹陷）。

这种频域建模方式不仅能压缩边界数据，还能通过系数实现形状的旋转、平移和尺度不变性。

1. 紧凑性与数据压缩
维度降低：原始形状边界由大量离散点表示（如图中众多黑点），数据量较大。通过傅里叶变换后，只需保留少数几个低频傅里叶系数就能近似描述形状。例如，对于一个复杂的多边形边界，可能有成百上千个顶点坐标，但用十几个甚至几个傅里叶系数就可勾勒出其大致轮廓，大大减少了数据存储量和传输带宽需求。

演示网站：https://www.longluo.me/projects/fourier/

几何变换不变性

平移不变性 ：当形状在平面内发生平移时，其傅里叶变换后的系数仅发生相位的平移，而幅值不变。这意味着无论形状在图像中的位置如何改变，通过分析傅里叶系数的幅值部分，都能识别出是同一个形状。比如一个圆形图案在图像中从左上角移动到右下角，其傅里叶描述子基本保持不变。
旋转不变性 ：形状旋转一定角度后，傅里叶系数的相位会相应改变，但可以通过对系数进行适当处理（如取模运算等），使得描述子不受旋转角度的影响。这对于在未知方向下识别形状非常有用，像卫星图像中不同朝向的建筑物识别。
尺度不变性 ：在一定尺度范围内，通过归一化傅里叶系数的某些参数（如第一个非零系数的幅值），可以使描述子对形状的大小变化不敏感。例如，不同大小的同一类零件，经过傅里叶描述处理后，可基于其形状特征进行统一分类。

3. 抗噪声能力
相比直接使用原始边界点进行形状分析，傅里叶描述在一定程度上具有抗噪声能力。噪声通常表现为边界上的微小扰动，在傅里叶变换后，这些高频噪声成分主要集中在高频系数中。通过适当滤除高频系数或者对低频系数进行分析，可以在一定程度上忽略噪声的影响，依然准确地描述形状的本质特征。

3. 区域描述

前言

定义

在前两节中，我们学习了边界描述的两类方法：

通过链码记录边界像素的连接方向（像用“东南西北”的步数描述行走路线），
通过傅里叶描述将边界曲线转换到频域，用低频-高频系数捕捉整体轮廓与细节特征。

这些方法本质上都是从“边界”（即形状的外围线条）入手，提取能反映形状宏观结构的特征。

但实际场景中，我们不仅关心“边界怎么走”（边界描述），更关心“形状是什么样”（整体几何属性），比如：判断一个图形是“圆”还是“方”，不仅要看它的边缘路径，还要看它的整体大小（面积）、对称性（是否各向均匀）、紧凑程度（是否接近圆形）等内在几何特性。这些特性被称为几何特征，它们是形状最基础的“标签”，也是后续形状分类、识别的关键依据。

更进一步，当我们希望这些几何特征“不受拍摄角度、距离影响”时（比如无论手机正拍还是斜拍一个饭碗，都能认出它是“饭碗”），就需要引入不变矩——一类对平移、旋转、缩放等常见变换保持稳定的特征。

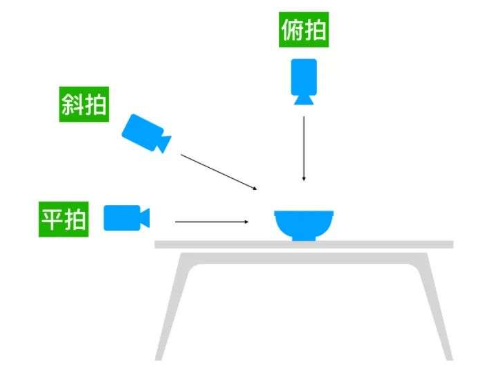
本节我们先学习几何特征（形状的基础直观属性），再理解不变矩（几何特征的升级版——抗干扰能力更强），逐步掌握描述形状本质的核心工具。

1. 几何特征：形状的直观几何属性

几何特征是最容易理解的形状描述方式--->它们直接对应我们肉眼观察到的“大小、多少、位置”等信息。
比如：看到一个苹果，我们会说“它直径约8厘米”（尺寸）、“表面光滑没有洞”（拓扑）、“两端稍微尖一点”（轮廓凹凸）；这些描述本质上都是几何特征。

区域面积
二值图像中的目标物面积A是目标物所占的像素点数
位置
由于目标在图中中总有一定面积的大小，因此有必要定义目标在图像中的精确位置。如形心，质心等
区域周长
区域周长是区域边界的长度。
方向
计算目标物体的方向比计算位置要复杂，因为某些形状（圆形）的方向并不是唯一。为了定义唯一的方向，一般假定物体是长方形的，并定义长轴方向为物体的方向。

距离
两个区域的距离，可以用他们的质心距离来计算。有欧式距离，4-邻域距离，8-邻域距离等。
圆形度
圆形度是圆形区域的面积与周长的比值。圆形度越大，表示区域越接近圆形。
矩形度
描述连通域与矩形相似程度的量。矩形度是矩形区域的面积与周长的比值。矩形度越大，表示区域越接近矩形。
长宽比
长宽比是矩形区域的长边与短边的比值。长宽比越大，表示区域越接近长方形。

2. 不变矩：几何特征的升级版

几何特征虽然直观，但有一个明显缺点：对变换敏感。比如你拍一张正方形的照片，如果手机倾斜拍摄（旋转）、站远一点（缩小）或移动位置（平移），它的“面积”“周长”数值可能不变，但“质心位置”“方向”会变——如果直接用原始几何特征（比如“边界的方向”），不同拍摄条件下的同一个正方形会被误判成不同形状。

矩：是概率论和统计学中用来描述数据分布特征的量，它反映了数据在各个位置上的加权平均。矩可以用来描述数据的集中趋势、离散程度、对称性等特性。矩的作用：用数学数字概括物体的形状。

但现实中，我们看物体常会「变角度」：

猫可能站着、躺着、侧身（旋转）；
拍照时手抖歪了（倾斜）；
离得近拍显大，离得远拍显小（缩放）；
甚至镜子里的倒影（镜像）。

**普通的「矩」**会跟着这些变化变：比如猫躺下了，重心位置变了，普通矩的值也会变，那我们用这组数字去识别猫时，就会认不出来。

不变矩就是为了解决这个问题诞生的：它是一组特殊的几何特征，无论形状如何平移、旋转或缩放，这些特征的数值都保持不变。就像给形状办了一张“身份证”，无论它怎么动、怎么变，身份证上的关键信息（如指纹）始终一致。

常用的不变矩是 7个，这里不列举数学公式（要看公式，教材的186页),但可以粗糙理解为它们分别对应：

描述“整体大小 ”的归一化特征；
描述“x/y方向胖瘦比例 ”的特征；
描述“倾斜程度 ”的特征；
描述“x方向对称性 ”的特征；
描述“y方向对称性 ”的特征；
描述“综合倾斜+对称性 ”的特征；
描述“高阶细节（如凹凸）”的特征。

例题9-1 对图像进行各种几何变换，观察不变矩的变化情况。 👇 👇

图像经过旋转、缩放、平移后的效果如图9-7所示。调用 moment_invariants()子函数可以求得图像的7个不变矩，在子函数中为了减小动态范围，将计算得到的不变矩取对数。各图像的不变矩如上表所示，可见图像经过各种几何变换后所求得的不变矩具有较好的一致性。

代码如下：

import numpy as np
import cv2
from matplotlib import pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负

img0 = cv2.imread(r'./img/lotus.jpg',0)
img=img0.copy()
textLists=[]  #用来存放几何变换名称
imgLists=[]   #用来存放几何变换图像
textLists.append("original")
imgLists.append(img)
# 旋转45度
rotate_45_matrix = cv2.getRotationMatrix2D((img.shape[1] // 2, img.shape[0] // 2), -45, 1)
rotate_45_image = cv2.warpAffine(img, rotate_45_matrix, dsize=(img.shape[1], img.shape[0]))
textLists.append("rotate-45")
imgLists.append(rotate_45_image)
# 平移
img=img0.copy()
M = np.float32([[1, 0, 50], [0, 1, 50]])
translation_img = cv2.warpAffine(img, M, dsize=(img.shape[1], img.shape[0]))
textLists.append("translation")
imgLists.append(translation_img)
# 顺时针旋转90
img=img0.copy()
rotate_90_iamge = cv2.rotate(img, rotateCode=cv2.ROTATE_90_CLOCKWISE)
textLists.append("rotate-90")
imgLists.append(rotate_90_iamge)
# 顺时针旋转180
img=img0.copy()
rotate_180_iamge = cv2.rotate(img, cv2.ROTATE_180)
textLists.append("rotate-180")
imgLists.append(rotate_180_iamge)
# 缩小一半
img=img0.copy()
resize_0_5_img=np.zeros(img.shape)
halfImg = cv2.resize(img, (img.shape[1] // 2, img.shape[0] // 2))
resize_0_5_img[0:halfImg.shape[0],0:halfImg.shape[1]]=halfImg
textLists.append("shrink  ")
imgLists.append(halfImg)
# 逆时针旋转90
img=img0.copy()
rotate_270_image = cv2.rotate(img, rotateCode=cv2.ROTATE_90_COUNTERCLOCKWISE)
textLists.append("rotate-270")
imgLists.append(rotate_270_image)

huMomentLists=[]
for img in imgLists:
    hu=moment_invariants(img)
    huMomentLists.append(np.array(hu))
    
for descipStr,hu in zip(textLists,huMomentLists):
    descipStr+="\t"
    for mm in hu:
        descipStr+="%0.2f"%mm+'\t'
    print(descipStr)

plt.figure(figsize=(10,5))
plt.subplot(241)
plt.imshow(img0,cmap="gray")
plt.title("原图像")
plt.axis("off")
plt.subplot(242)
plt.imshow(rotate_45_image,cmap="gray")
plt.title("旋转45度")
plt.axis("off")
plt.subplot(243)
plt.imshow(rotate_90_iamge,cmap="gray")
plt.title("顺时针旋转90")
plt.axis("off")
plt.subplot(244)
plt.imshow(rotate_180_iamge,cmap="gray")
plt.title("顺时针旋转180")
plt.axis("off")
plt.subplot(245)
plt.imshow(rotate_270_image,cmap="gray")
plt.title("逆时针旋转90")
plt.axis("off")
plt.subplot(246)
plt.imshow(resize_0_5_img,cmap="gray")
plt.title("缩小一半")
plt.axis("off")

plt.subplot(247)
plt.imshow(translation_img,cmap="gray")
plt.title("平移")
plt.axis("off")
plt.show()

4. 纹理描述

前言

定义

1. 矩分析法

通俗理解:把图像的灰度值看作一堆数字，计算它们的"统计特征"：

一阶矩：平均灰度（整体亮度）
二阶矩：方差（对比度，灰度变化剧烈程度）
三阶矩：偏斜度（分布对称性，偏向亮还是暗）
四阶矩：峰度（分布尖锐程度，是否有很多极值）

纹理越粗糙，灰度变化越大，高阶矩的值通常也越大

import cv2
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

def moment_analysis(image):
    """
    矩分析法纹理描述
    """
    # 确保是灰度图
    if len(image.shape) == 3:
        gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    else:
        gray = image.copy()
    
    # 计算各阶中心矩
    moments = {}
    
    # 零阶矩（总灰度值）
    m00 = np.sum(gray)
    moments['m00'] = m00
    
    # 一阶矩（重心）
    height, width = gray.shape
    x_coords = np.arange(width)
    y_coords = np.arange(height)
    
    m10 = np.sum(x_coords * np.sum(gray, axis=0))
    m01 = np.sum(y_coords * np.sum(gray, axis=1))
    
    x_centroid = m10 / m00 if m00 != 0 else 0
    y_centroid = m01 / m00 if m00 != 0 else 0
    
    moments['centroid'] = (x_centroid, y_centroid)
    
    # 二阶矩（惯性矩/对比度相关）
    x_grid, y_grid = np.meshgrid(x_coords, y_coords)
    mu20 = np.sum(((x_grid - x_centroid)**2) * gray)
    mu02 = np.sum(((y_grid - y_centroid)**2) * gray)
    mu11 = np.sum((x_grid - x_centroid) * (y_grid - y_centroid) * gray)
    
    moments['mu20'] = mu20  # x方向分布
    moments['mu02'] = mu02  # y方向分布  
    moments['mu11'] = mu11  # 相关性
    
    # 统计矩（更直观的纹理描述）
    flat_gray = gray.flatten()
    
    moments['mean'] = np.mean(flat_gray)      # 一阶矩：平均灰度
    moments['variance'] = np.var(flat_gray)   # 二阶矩：对比度
    moments['skewness'] = stats.skew(flat_gray) # 三阶矩：偏斜度
    moments['kurtosis'] = stats.kurtosis(flat_gray) # 四阶矩：峰度
    
    return moments

# 使用示例1 
image = cv2.imread('./img/star.png')

# 使用示例2
image = cv2.imread('./img/star11111.png')

moments = moment_analysis(image)

print("矩分析结果:")
for key, value in moments.items():
    if isinstance(value, tuple):
        print(f"{key}: ({value[0]:.2f}, {value[1]:.2f})")
    else:
        print(f"{key}: {value:.4f}")

矩分析结果:

m00: 40482525.0000  # 总灰度值
centroid: (267.02, 170.38) # 重心
mu20: 1090391467859.2772 # x方向分布
mu02: 439412917170.5587 # y方向分布
mu11: 16838846.5588 # 相关性
mean: 221.6666 # 一阶矩：平均灰度
variance: 7388.9044 # 二阶矩：对比度
skewness: -2.1910 # 三阶矩：偏斜度
kurtosis: 2.8004 # 四阶矩：峰度

核心思想 :用统计矩描述纹理的灰度分布规律
优点：计算简单，物理意义明确
缺点：对复杂纹理描述能力有限
应用场景 ：简单纹理分析、预处理

2. 灰度差分析法

通俗理解: 看相邻像素之间的灰度差异

相邻像素灰度差大 → 纹理粗糙、棱角分明（如砂纸）
相邻像素灰度差小 → 纹理平滑、细腻（如丝绸）
特定方向的灰度差突出 → 纹理有方向性（如木纹、布纹）

常用指标：灰度差绝对值之和、灰度差平方和（类似梯度能量）。

def gray_difference_analysis(image, distance=1):
    """
    灰度差分析法纹理描述
    """
    if len(image.shape) == 3:
        gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    else:
        gray = image.copy()
    
    height, width = gray.shape
    directions = {
        'horizontal': (0, 1),    # 0°
        'vertical': (1, 0),      # 90° 
        'diagonal_45': (1, 1),   # 45°
        'diagonal_135': (1, -1)  # 135°
    }
    
    results = {}
    
    for direction, (dx, dy) in directions.items():
        diff_sum = 0
        diff_sq_sum = 0
        count = 0
        
        for y in range(height - abs(dy)*distance):
            for x in range(width - abs(dx)*distance):
                # 当前像素
                current = gray[y, x]
                # 相邻像素（考虑距离和方向）
                neighbor = gray[y + dy*distance, x + dx*distance]
                
                # 计算绝对差和平方差
                diff_abs = abs(current - neighbor)
                diff_sq = (current - neighbor) ** 2
                
                diff_sum += diff_abs
                diff_sq_sum += diff_sq
                count += 1
        
        # 归一化（除以像素对数）
        results[f'{direction}_abs_mean'] = diff_sum / count if count > 0 else 0
        results[f'{direction}_energy'] = diff_sq_sum / count if count > 0 else 0
    
    # 总体粗糙度（所有方向平均）
    all_diffs = list(results.values())
    results['overall_roughness'] = np.mean(all_diffs)
    
    return results

# 使用示例1  纹理粗糙的
diff_results = gray_difference_analysis(image)
# 使用示例2  纹理细腻的

# 使用示例3  木纹

print("\n灰度差分析结果:")
for key, value in diff_results.items():
    print(f"{key}: {value:.4f}")

灰度差分析结果:

horizontal_abs_mean: 0.0000 # 水平方向灰度差绝对值之和
horizontal_energy: 0.0008 # 水平方向灰度差平方和
vertical_abs_mean: 0.0000 # 垂直方向灰度差绝对值之和
vertical_energy: 0.0004 # 垂直方向灰度差平方和
diagonal_45_abs_mean: 0.0000 # 45°方向灰度差绝对值之和
diagonal_45_energy: 0.0007 # 45°方向灰度差平方和
diagonal_135_abs_mean: 0.0000 # 135°方向灰度差绝对值之和
diagonal_135_energy: 0.0007 # 135°方向灰度差平方和
overall_roughness: 0.0003 # 总体粗糙度

核心思想：分析像素间灰度的变化频率和幅度
优点：能捕捉纹理的粗糙度、方向性
缺点：对噪声敏感，参数选择重要
应用场景：方向性纹理、边缘检测

3. 灰度共生矩阵法（GLCM）

通俗理解:最强大的纹理分析方法！核心是：统计"相距一定距离、成特定角度的两个像素，灰度值分别为i和j"这种情况出现的次数。
比如：

看所有"右边相邻像素"（距离=1，角度=0°）的组合
统计(灰度=10, 灰度=50)出现了多少次，(灰度=20, 灰度=20)出现了多少次...
形成一个矩阵，这个矩阵就包含了纹理的空间关系信息

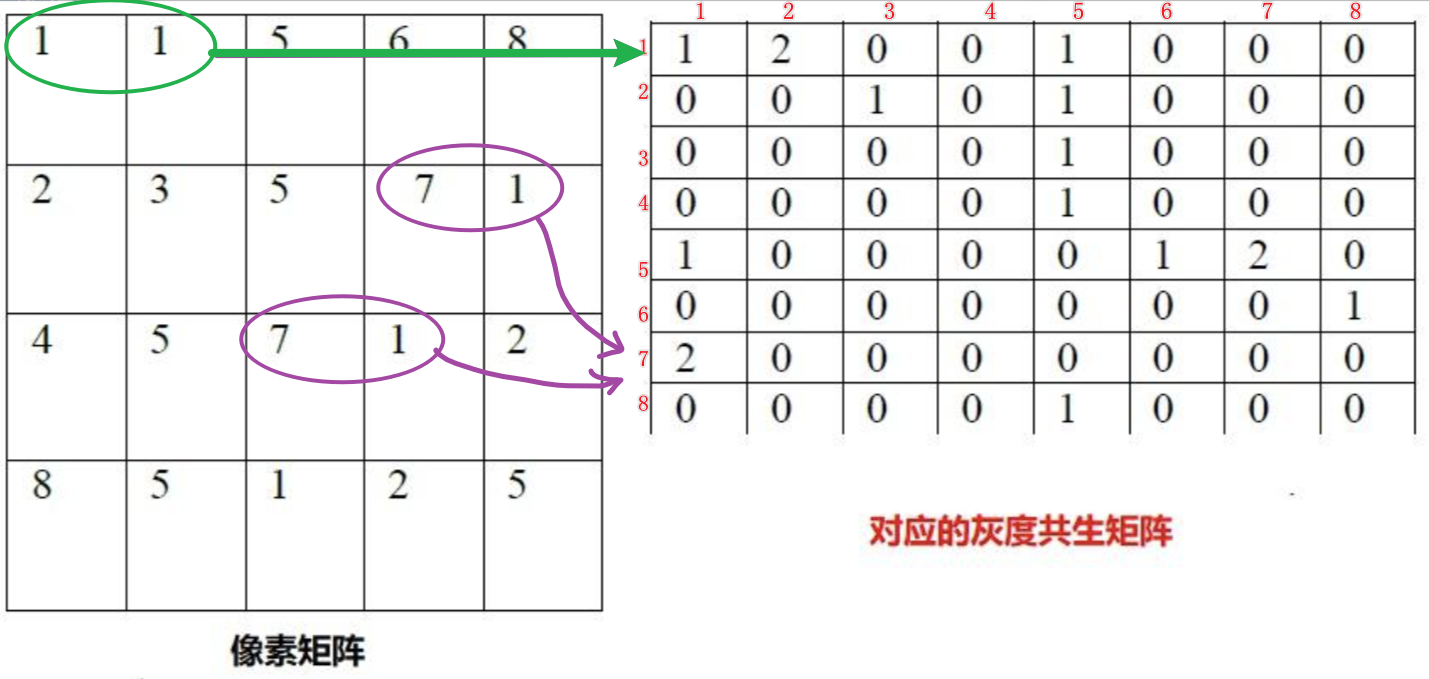
从这个矩阵可以提取：对比度、能量、熵等14种特征。

核心思想： 统计特定空间关系下像素对的出现概率
优点 ：描述能力强，理论基础坚实
缺点 ：计算量大，参数多
适用场景： 复杂纹理分类、识别

第九章 图像描述和特征提取

第九章图像描述和特征提取