第五章 图像复原
- 边缘检测和连接
- 边缘检测
- 边缘连接
- 区域分割
- 区域生长
- 区域分裂与合并
1. 边缘检测和连接
1.1 边缘检测
前言
在教材的3.6节介绍了一些空域锐化滤波,常用来进行边缘检测。图像的边缘是由于相邻像素间灰度值剧烈变化引起的。
一阶的梯度算子:
- 梯度算子(Gradient operators)
- 拉普拉斯算子(Laplacian operator)
- Sobel算子(Sobel operator)
但是一阶的梯度算子在图像边缘处会出现一些噪声,所以在实际应用中,常用二阶的梯度算子来进行边缘检测。
- 其中将有平滑效果的高斯滤波器和拉普拉斯算子结合起来,可以得到一个平滑效果好,边缘检测效果好的算子,称为DoG算子(Difference of Gaussian)。
- 还有1986年Canny提出的边缘检测算子Canny算法,他认为边缘算子必须满足以下几个条件:
- 低错误率
- 定位精度
- 单边响应
1.2 边缘连接
前言
Canny算法通过 梯度计算→非极大值抑制→双阈值检测→边缘连接等步骤,能够得到较为精细的边缘图,但在实际应用中(尤其是文档图像、低质量扫描件或复杂背景中),我们常常会遇到一个问题:👇
检测到的边缘是“断断续续”的!
比如: ✏️
- 文档中的文字笔画较细,边缘可能因为噪声、光照或扫描模糊而断裂(例如字母 "i" 的点和竖线分开、汉字笔画断开);
- 目标物体的轮廓因遮挡、反光或低对比度出现局部缺失;
- 图像边缘检测后,本应连续的边界被分成多段短边缘,导致后续的分割、识别或测量任务失败。
这时候,就需要用到 边界连接(Edge Linking)技术
它的核心目标是:把检测到的断裂边缘片段“连接”起来,形成更完整、连续的边界,从而提升后续分割或分析的准确性。
边界连接方法按作用范围和处理策略的不同,主要分为以下三类:
- 局部的边界连接
- 区域的边界连接
- 全局的边界连接
1.局部的边界连接
核心思想:只关注边缘像素的“邻域局部信息”(比如周围几个像素),通过分析相邻边缘点之间的关系,直接连接距离近、方向一致的短边缘片段。
适用场景:
- 边缘断裂发生在局部小范围内(比如几个像素的间隔);
- 图像噪声较少,边缘梯度方向较明确;
- 需要快速处理,对计算效率要求较高。
常见方法:
基于距离与方向的简单连接
策略: 对于每一个边缘像素点,检查其 3×3 或 5×5 邻域内是否存在其他边缘点,如果存在且两者之间的欧氏距离很近(如<3像素)、并且梯度方向相近(夹角<一定阈值,如30°),则认为它们属于同一条边缘,直接将它们连接(例如通过插值补线段或标记为连通)。
邻域像素搜索与链码跟踪
策略:从某个边缘点出发,沿着其梯度方向(或反方向)在邻域内搜索下一个边缘点,逐步“跟踪”出一条连续的边缘链(类似“贪心算法”)。
直观例子:
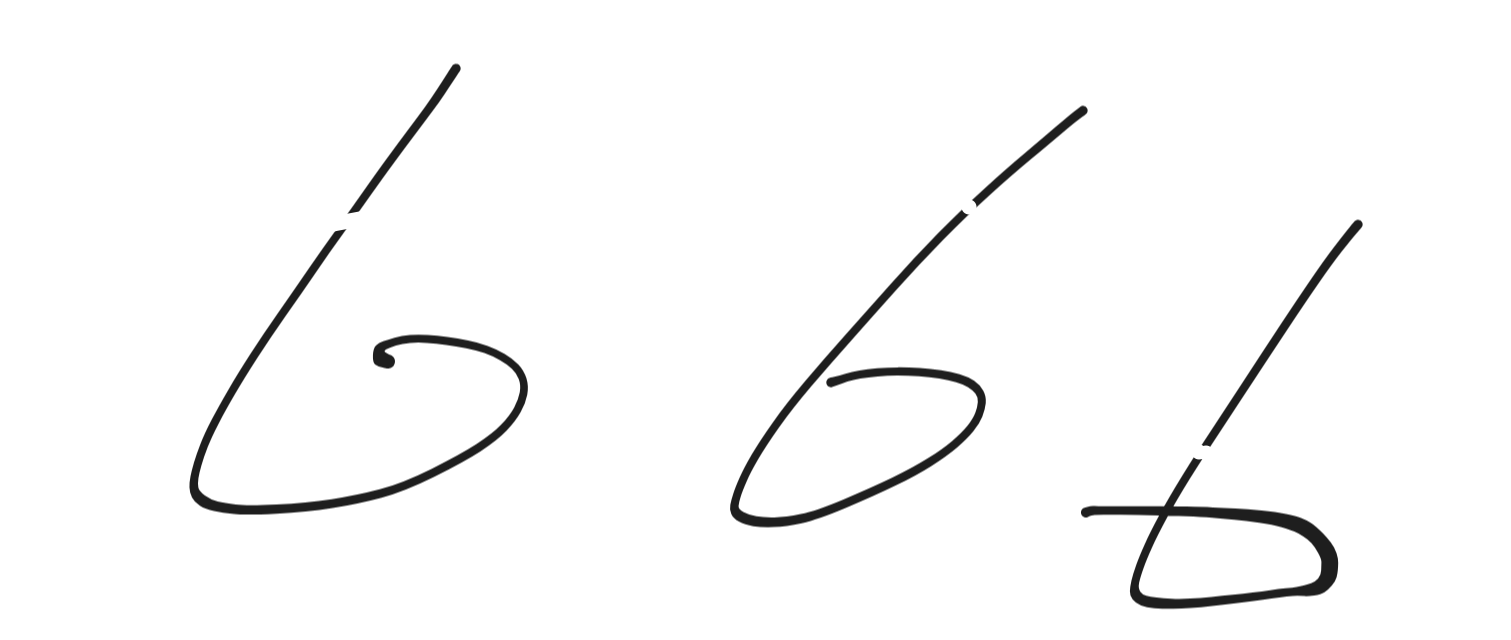
想象你用笔在纸上画了一条连续的直线(或曲线),但由于纸有点皱、笔尖力道不均,或者拍照时焦点没对准,导致这条线在图像中中间部分看起来淡了一些(或模糊了一些),用 Canny 检测边缘时,两端的边缘被检测出来了,但中间部分的弱边缘被过滤掉了,于是这条线在边缘图上看起来像是“断成了两截”。
此时,边界连接算法的作用,就是发现这两截边缘其实属于同一条线(方向一致、距离近、灰度相似),然后把它们“连接”起来,还原出原本连续的边界,为后续的分割、识别等任务提供更完整的信息。
评价:计算复杂度高,因为要判断邻域中所有点是否与中心像素点相连接
2.区域的边界连接
上面介绍了局部的边界连接,它通过分析边缘像素邻域(如几个像素的周围)的方向和距离,快速缝合那些近在咫尺 的断裂边缘(比如间隔仅2-3像素的片段)。但若断裂范围稍大(如间隔10像素)、或局部邻域信息因噪声模糊时,仅靠“几个像素的邻居”可能判断不准——比如方向稍偏差、或噪声干扰导致误连。
这时就需要升级到区域的边界连接:它不再只看单个像素的邻域,而是观察断裂边缘所在的小块区域(如10×10像素块),通过分析该区域的整体灰度、纹理或边缘密度,判断断裂处两侧是否属于同一物体(比如文字笔画或物体轮廓的连续部分),从而更可靠地连接稍大范围的断裂。
**核心思想:**不再只看单个边缘像素的邻域,而是考虑边缘所在的“局部区域”(如小块图像区域)的整体特征(如灰度、纹理、边缘密度),通过区域内的上下文信息推断并连接断裂的边缘。
适用场景:
- 边缘断裂发生在稍大范围(如10~30像素),但断裂区域周围的灰度/纹理具有连续性(比如文字笔画虽断但背景灰度一致);
- 需要结合边缘和区域信息(如边缘强度+局部灰度相似性)提高连接准确性;
- 对局部噪声有一定鲁棒性。
鲁棒性: 在某种程度上,即使出现一些小的错误,也能继续运行。
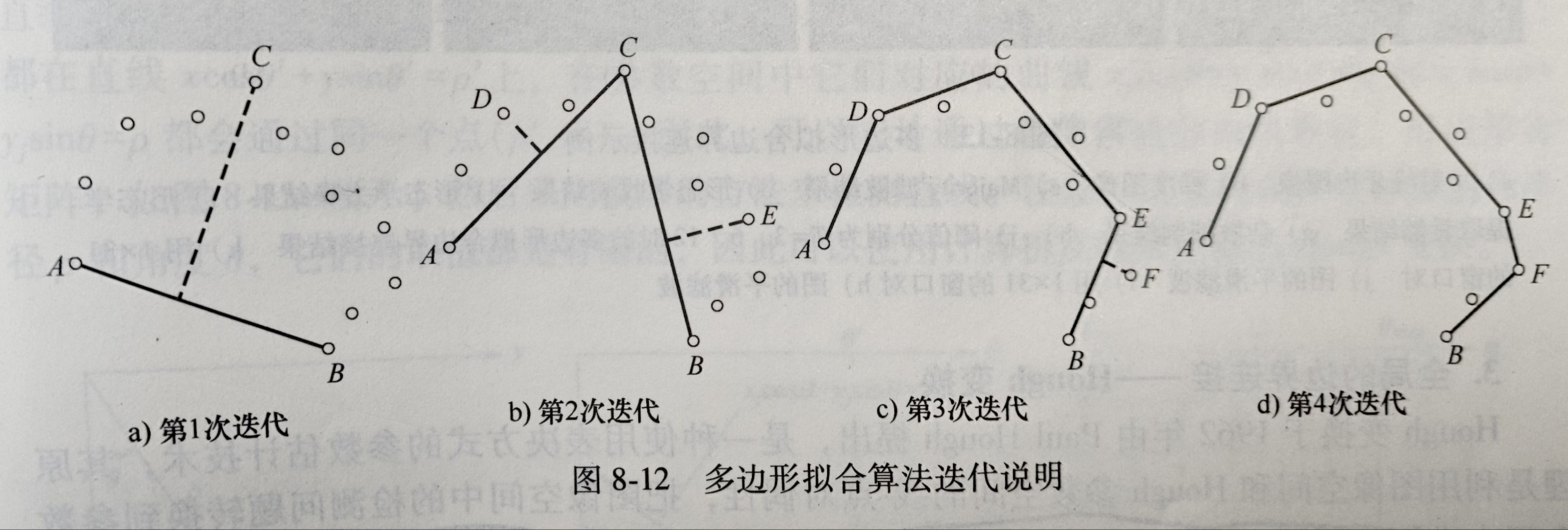
3.全局的边界连接
实际场景中,还存在更复杂的挑战:
- 断裂跨度大:比如文档中因严重模糊或遮挡,文字笔画或物体轮廓的边缘被分成相隔数十像素的多段片段;
- 全局拓扑复杂:目标边界可能包含弯曲、交叉或分叉结构(如汉字“口”的闭合轮廓、地图中的道路网络),局部/区域方法难以推断全局最优连接路径;
- 多目标干扰:图像中存在多个相邻目标(如密集文字或零件群),局部信息易误连不同目标的边缘片段。
这时就需要全局的边界连接(Global Edge Linking)——它跳出局部或区域的限制,从整幅图像的全局视角出发,综合考虑所有边缘片段的空间位置、方向、曲率甚至语义信息,通过全局优化算法推断出最可能的完整边界,实现大跨度、高精度的断裂连接。
在全局边界连接技术中,霍夫变换(Hough Transform) 是一种经典且高效的算法,尤其擅长处理规则几何形状(如直线、圆、椭圆)的边缘断裂连接问题。它通过将图像中的边缘点从“笛卡尔坐标系(x-y平面)”转换到“参数空间(如角度-截距平面)”,利用全局投票机制找到最可能的完整几何形状,从而将分散的断裂边缘片段“缝合”成一条连续的规则边界。
霍夫变换是全局边界连接技术中针对规则形状的“杀手锏”——它通过将图像中的边缘点映射到参数空间并利用全局投票机制,精准捕捉直线、圆等几何形状的全局特征,从而高效连接因模糊、遮挡或噪声导致的断裂边缘片段。
案例:
发票校正案例:👇
import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负
# 发票校正函数
def hough_correct_invoice_optimized(image_path, output_path=None, delta_angle=3.0):
img = cv2.imread(image_path)
if img is None:
raise ValueError("图片加载失败,请检查路径!")
original = img.copy()
h, w = img.shape[:2]
# 1. 二值化优化(自适应阈值,调整blockSize和C)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
binary = cv2.adaptiveThreshold(
gray, 255,
cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
cv2.THRESH_BINARY_INV,
blockSize=15, # 增大blockSize(适应光照不均)
C=3 # 增大C(增强对比度)
)
# 2. 边缘检测(直接用二值图,或可选Canny)
edges = binary # 直接用二值图(文本/表格线为白色)
# 3. 霍夫变换参数放宽(检测更多线段)
lines = cv2.HoughLinesP(
edges,
rho=1,
theta=np.pi/180,
threshold=30, # 降低投票阈值
minLineLength=20, # 允许更短线段
maxLineGap=10 # 连接更大间隙
)
# 4. 提取并分析角度
angles = []
if lines is not None:
for line in lines:
x1, y1, x2, y2 = line[0]
angle = np.degrees(np.arctan2(y2 - y1, x2 - x1))
angles.append(angle)
if not angles:
print("未检测到有效直线!请检查二值化参数。返回原图。")
return original
angles_array = np.array(angles)
mean_angle = np.mean(angles_array)
std_angle = np.std(angles_array)
print(f"检测到的角度:均值={mean_angle:.2f}°, 标准差={std_angle:.2f}°")
# 5. 放宽角度容差(避免过滤真实倾斜)
valid_angles = angles_array[
(angles_array >= mean_angle - delta_angle) &
(angles_array <= mean_angle + delta_angle)
]
final_angle = np.mean(valid_angles)
print(f"过滤后主流角度:±{delta_angle}°, 最终校正角度={final_angle:.2f}°")
# 6. 旋转校正
center = (w // 2, h // 2)
rotation_matrix = cv2.getRotationMatrix2D(center, final_angle, 1.0)
rotated = cv2.warpAffine(
original,
rotation_matrix,
(w, h),
borderValue=(255, 255, 255)
)
# # 7. 保存与显示
if output_path:
cv2.imwrite(output_path, rotated)
print(f"校正后的图片已保存至:{output_path}")
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.imshow(cv2.cvtColor(original, cv2.COLOR_BGR2RGB))
plt.title(f'原始发票(倾斜约{final_angle:.1f}°)')
plt.axis('off')
plt.subplot(1, 2, 2)
plt.imshow(cv2.cvtColor(rotated, cv2.COLOR_BGR2RGB))
plt.title(f'校正后(补偿{-final_angle:.1f}°)')
plt.axis('off')
plt.tight_layout()
plt.show()
return rotated
# 使用示例
input_image = "./img/table.png" # 替换为您的发票路径
output_image = "invoice_corrected_optimized.jpg"
corrected_img = hough_correct_invoice_optimized(input_image, output_image, delta_angle=3.0)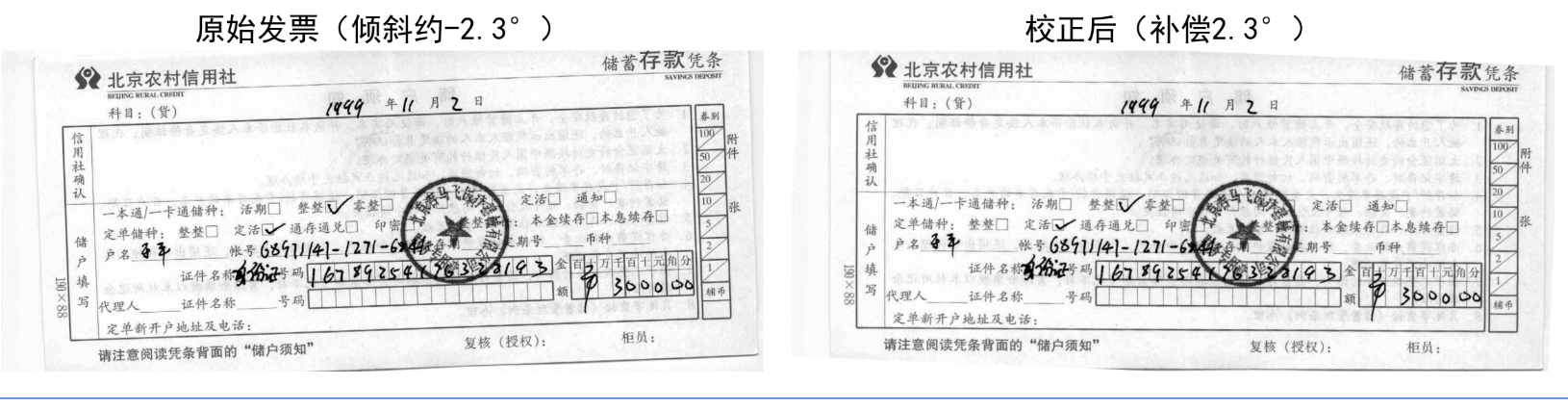
2. 区域分割
2.1 区域生长
前言
在前面的边界连接技术中,我们主要关注如何连接断裂的边缘或线条,让目标的轮廓更完整。但有时候,我们的目标不仅仅是“画出边界”,而是要直接把图像中具有相似特征(如灰度、颜色、纹理)的像素聚合成一个完整的区域(比如文档中的文字区域、医学图像中的器官、工业零件中的缺陷块)。
这时候,就需要用到 区域分割 技术,而 区域生长 是其中最经典、最直观的方法之一。
区域生长的核心思想是“相似像素聚合”
但它并不单一,而是可以根据不同的“相似性判断标准”细分为多种策略。接下来,我们将从三个经典维度展开讲解:
- 基于区域灰度差的生长(最基础的像素级相似)
- 基于区域内灰度分布统计性质的生长(考虑整体统计特征)
- 基于区域形状的生长(引入结构化约束),逐步深入区域生长的多维度应用。
1. 基于区域灰度差的生长
最初的区域生长方法非常直观——它不考虑复杂的统计特性,也不关心区域的整体形状,而是只关注像素与邻居之间最朴素的灰度差异:如果一个像素和它已经属于目标区域的“邻居”灰度值很接近,那它大概率也属于同一目标。这种基于“局部灰度差”的生长策略,是区域生长的最基础形式,也是理解后续复杂方法的基础。
核心思想: 👇
基于区域灰度差的生长,其核心判断标准是:待生长的像素与当前已生长区域的边界像素(或区域平均灰度)之间的灰度差是否小于某个预设阈值。如果满足,则认为该像素与区域相似,将其纳入区域;否则拒绝。
典型实现逻辑
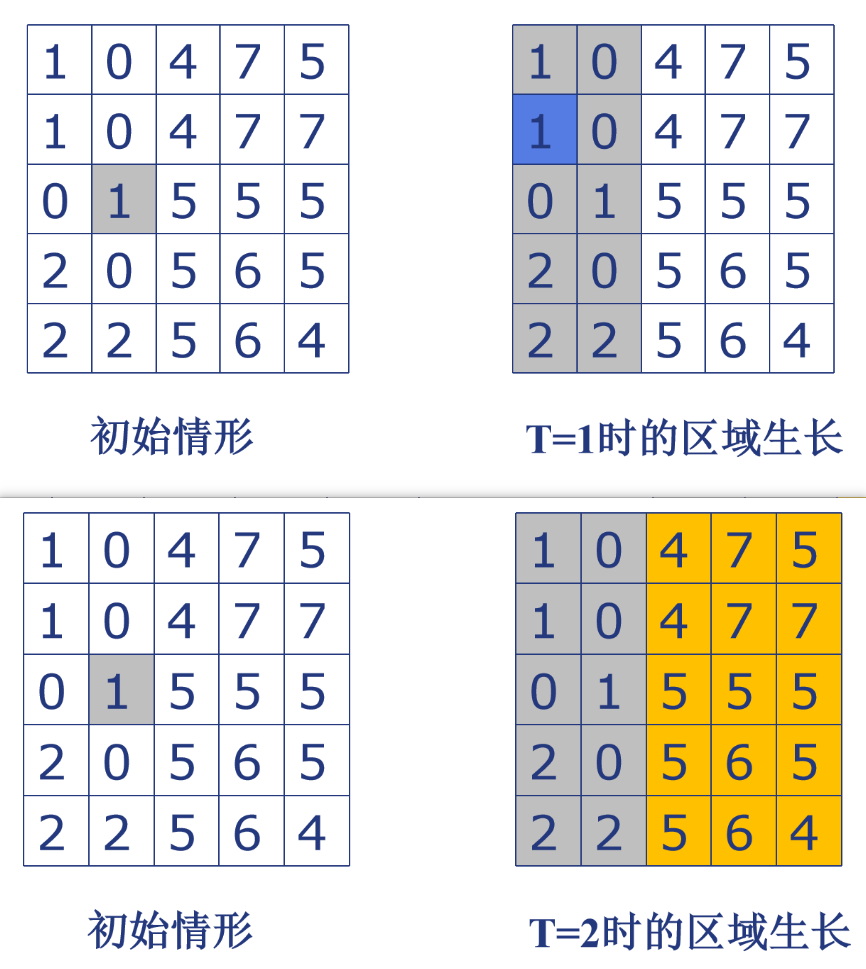
- 种子点选择:用户手动或自动选取若干个“肯定属于目标”的像素(如文档中文字笔画的一个深色像素)。
- 生长阈值(T):设定一个灰度差阈值(如10),表示新像素与已生长区域的灰度允许的最大差异。
- 生长过程:
- 从种子点开始,标记其为已生长;
- 对于每个已生长像素,检查其邻域(4邻域或8邻域)内的未生长像素;
- 若邻域像素的灰度值与当前已生长区域的平均灰度(或边界像素灰度)的差值 ≤ T,则将该邻域像素纳入区域,并更新区域平均灰度;
- 重复直到没有新像素满足条件。
适用场景与优势 : 👇
适合: 光照较均匀、目标与背景灰度差异明显的图像(如文档中的黑白文字)。
局限: 对局部灰度波动敏感(比如文字笔画中因纸张褶皱导致的局部深浅变化可能被误判为不相似);仅依赖单一灰度差,无法处理复杂统计特性(如灰度分布偏斜)。
2. 基于区域内灰度分布统计性质的生长
当图像中目标与背景的灰度差异不均匀,不仅看单个像素的灰度值,还要分析整个已生长区域的灰度统计特性(如均值、方差),并通过对比新像素与区域统计分布的匹配程度来决定是否生长。
核心思想: 👇
基于区域内灰度分布统计性质的生长,其核心是通过计算已生长区域的灰度统计特征(如均值μ、方差σ²),并定义一个统计相似性准则(如新像素灰度值落在区域均值±k×标准差的范围内),来判断新像素是否属于同一目标。
典型实现逻辑
- 种子点选择与初始化:同前,选取种子点并标记为已生长,初始化区域的像素集合。
- 统计特征计算:在每次迭代中,动态计算已生长区域的灰度均值(μ)和方差(σ²)(或仅均值)。
- 生长条件:对于邻域内的未生长像素,判断其灰度值是否符合以下任一统计准则:
- 均值±阈值法 :若 |新像素灰度 - μ| ≤ T(T为固定阈值,如15),则纳入;
- 标准差约束法 :若 |新像素灰度 - μ| ≤ k×σ(k为系数,如2~3),则纳入(考虑灰度分布的离散程度);
- 高斯分布匹配 (更复杂):假设区域灰度服从高斯分布,计算新像素属于该分布的概率,若概率高于阈值则纳入。
- 动态更新:每纳入一个新像素,重新计算区域的μ和σ²,用于下一轮判断。
适用场景与优势 : 👇
适合 :目标灰度分布不均匀(如文档中因阴影导致文字局部深浅变化)、或需要区分多目标(如背景与文字的灰度分布差异显著)的场景。
优势 :通过统计特性更全面地描述区域特征,对局部噪声和灰度波动更鲁棒;可区分灰度均值相近但分布不同的区域(如浅色文字与浅色背景)。
3. 基于区域形状的生长
前两种方法主要关注像素的“灰度相似性” ,但实际场景中,目标区域往往还具有特定的形状或空间结构(比如文档中的文字通常是连通的、规则的块状区域,而非零散的像素簇;医学图像中的器官可能有平滑的边界)。如果仅依赖灰度相似性生长,可能会把形状不连续的噪声像素误纳入区域,或无法区分灰度相似但结构不同的目标(比如两个灰度相近但形状分离的物体)。这时,我们需要引入形状约束——在灰度相似的基础上,进一步要求生长的区域满足特定的形状规则。
核心思想: 👇
基于区域形状的生长,在灰度相似性判断的基础上,增加了对区域形状特征(如连通性、面积、边界曲率、紧凑度)的约束。例如:只允许生长出连通的像素块;限制区域的面积范围(避免过小噪声块);要求边界尽量平滑(排除锯齿状伪区域)。
4. 案例代码:
import numpy as np
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负
#定义区域生长函数
def regionGrow(img,p1,p2):
#p1,p2分别是两个种子点的坐标
img_array = np.array(img)#图片转为数组方便操作
[m,n]=img_array.shape#返回图片的长和宽
a = np.zeros((m,n)) #建立等大小空矩阵
a[p1]=1 #设立种子点
a[p2]=1
k = 30 #设立生长阈值
is_My_Area=1
while is_My_Area==1: #当区域生长时
is_My_Area=0 #初始化区域生长标志为0
lim = (np.cumsum(img_array*a)[-1])/(np.cumsum(a)[-1]) #计算区域平均灰度
for i in range(2,m-2): #遍历区域
for j in range(2,n-2): # 遍历区域
if a[i,j]==1:#如果该点已经属于区域
for x in range(-1,2):
for y in range(-1,2):
if a[i+x,j+y]==0: #如果该点未属于区域
if (abs(img_array[i+x,j+y]-lim)<=k) :
is_My_Area = 1 #
a[i+x,j+y]=1
data = img_array*a #矩阵相乘获取生长图像的矩阵
# new_img = Image.fromarray(data) #data矩阵转化为二维图片
return data
image0 = cv2.imread(r'./img/lung.jpg',0)
plt.figure(figsize=(10,4))
plt.subplot(1,3,1)
plt.axis("off")
plt.imshow(image0,vmin=0, vmax=255,cmap = plt.cm.gray)
plt.title('原图像')
image1= regionGrow(image0,(100,100),(100,250))
plt.subplot(1,3,2)
plt.imshow(image1,vmin=0, vmax=255,cmap = plt.cm.gray)
plt.title('生长图像')
plt.axis("off")
plt.subplot(1,3,3)
aa=image0[100:200,250:300]
plt.imshow(aa,cmap="gray")
plt.title('局部图像')
plt.axis("off")
plt.show()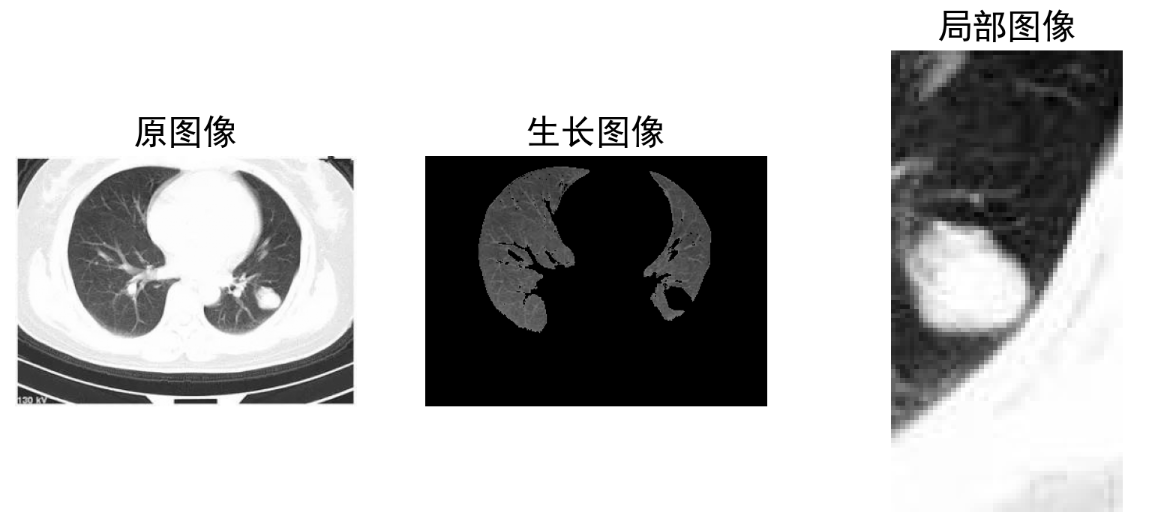
2.2 区域分裂与合并
前言
在前面的区域生长技术中,我们围绕“如何从种子点出发,通过相似性聚合像素形成完整区域”展开,核心逻辑是“自下而上”地生长——先有种子,再逐步合并邻居像素。
但这种方法依赖种子点的选择,且对复杂图像(如目标与背景灰度交错、多目标紧密相邻)可能不够灵活:如果初始种子选得不好,可能漏掉部分目标或误合并背景;如果图像中存在多个灰度差异显著的目标,单一生长策略难以同时处理。
这时,我们需要一种更“智能”的分割思路——不依赖预先设定的种子点,而是先对图像进行全局划分,再根据局部区域的特征动态决定是否拆分(分裂)或合并相邻区域,最终得到一组语义合理的分割块。这种方法就是 分裂合并法,它是区域分割中“自上而下+自下而上”结合的经典策略。
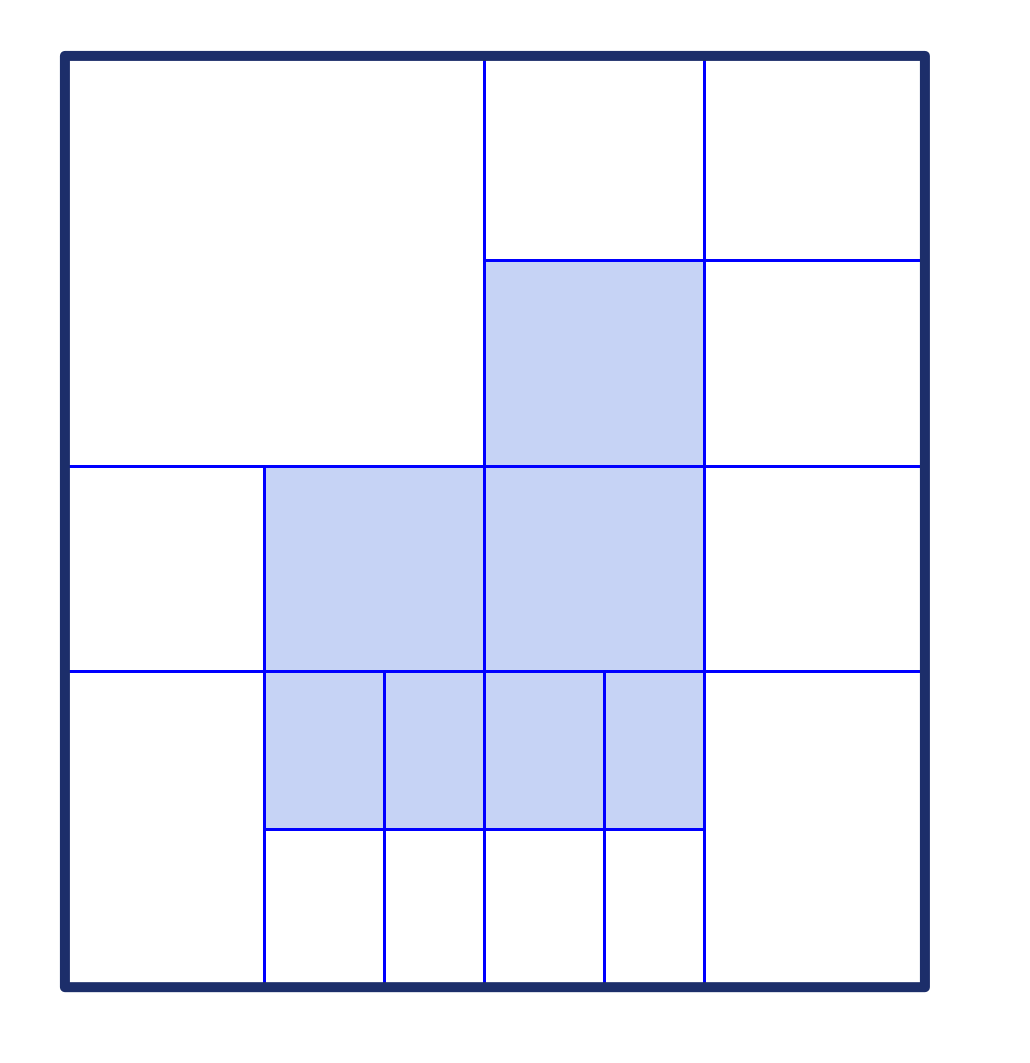
分裂合并法的解决思路是:先不管细节,把整幅图像当作一个“粗糙的整体区域”,然后逐步拆分成更小的子区域(分裂),再把相似的子区域合并成有意义的目标区域(合并)。它不依赖种子点,而是通过分析每个区域的内部一致性,动态决定如何拆分与组合,最终实现更自适应的分割。
2.3 图像水域分割
前言
之前的区域生长和分裂合并法,本质上都是基于“像素或区域的相似性”进行分割:区域生长依赖“邻居像素灰度接近”逐步聚合,分裂合并法依赖“区域内部统计特征一致”或“邻域区域相似”。但这些方法在面对目标边界模糊(如文字笔画因墨水扩散而粘连)、多个目标物理接触(如文档中相邻的两个印章重叠)时,容易出现两个问题:
- 过度分割(Over-segmentation):把一个完整的目标拆分成多个小块(比如一个文字被误分成几段);
- 欠分割(Under-segmentation):把多个相邻目标合并成一个区域(比如两个接触的印章被误认为一个整体)。
水域分割的解决思路完全不同——它不直接分析像素的灰度相似性,而是将图像转换为“地形高度图”,通过模拟水的流动路径自然形成目标边界。这种方法对边界模糊和目标接触的场景更鲁棒,能更精准地保留目标的完整性。
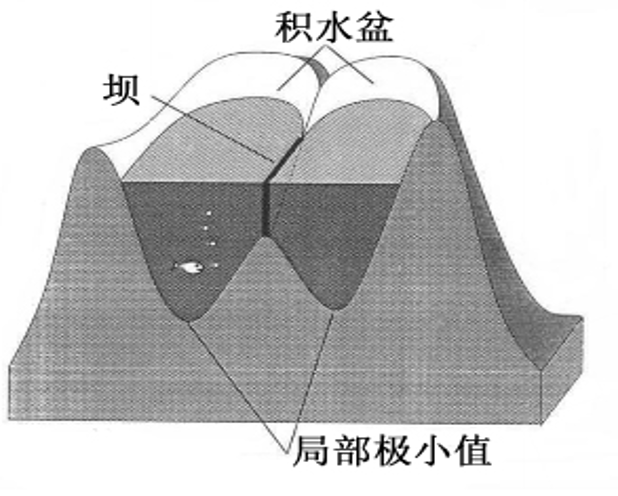
水域分割的基本思想是基于局部极小值和积水盆的概念。
积水盆是地形中局部极小点的影响区,水平面从这些局部极小值 处上涨,在水平面浸没地形的过程中,每一个积水盆被筑起的“坝 ”所包围,这些坝用来防止不同积水盆里的水混合到一起。在地形完全浸没到水中之后,这些筑起的坝 就构成了分水岭 。
水域分割的核心隐喻是:把图像的灰度值看作地形的高度(像素越亮,高度越高;像素越暗,高度越低),而分割的目标是找到“山峰”(目标)和“山谷”(背景)之间的自然分水岭(边界)。
代码演示: 👇
下面的代码实现了 基于水域分割(Watershed算法)的硬币分割。核心目标是通过模拟水的自然扩散过程,将紧密接触的硬币分割成独立的区域,避免传统阈值法导致的粘连问题。
代码主要流程:
- 图像预处理:灰度化 → Otsu阈值二值化(反色)→ 开运算去噪。
- 确定背景/前景/未知区域:通过膨胀确定背景,距离变换+阈值确定前景,剩余部分为未知区域。
- 标记生成:连通域标记前景 → 未知区域标记为0 → 调用 cv2.watershed执行分水岭分割。
- 结果可视化:展示开运算、背景、前景、未知区域、标记图和最终分割图。
import numpy as np
import cv2
from matplotlib import pyplot as plt
# 设置Matplotlib支持中文显示(避免坐标轴标签乱码)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
# ===================== 1. 读取图像并灰度化 =====================
img = cv2.imread(r'./img/coin.jpg') # 读取硬币图像(路径替换为实际路径,如 'coin.jpg')
if img is None:
raise FileNotFoundError("图片加载失败,请检查路径是否正确!")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 转为灰度图(水域分割基于灰度信息)
# ===================== 2. Otsu阈值二值化(反色)=====================
ret, thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU)
# 作用:自动计算阈值,将硬币(目标)转为黑色(0),背景转为白色(255)
# 若硬币为浅色(目标比背景亮),需去掉 THRESH_BINARY_INV 或调整后续步骤
# ===================== 3. 开运算去噪 =====================
kernel = np.ones((3, 3), np.uint8) # 3x3方形结构元素(用于形态学操作)
opening = cv2.morphologyEx(thresh, cv2.MORPH_OPEN, kernel, iterations=2)
# 作用:先腐蚀后膨胀,移除小噪声点(如灰尘、扫描噪点)
# 迭代次数可根据噪声量调整(一般1~3次)
# ===================== 4. 确定背景区域 =====================
sure_bg = cv2.dilate(opening, kernel, iterations=3)
# 作用:对开运算结果膨胀,扩展背景区域(确保背景被完全标记)
# 迭代次数影响背景覆盖范围(粘连硬币时需足够大,避免背景边缘误判)
# ===================== 5. 确定前景区域(距离变换 + 阈值)=====================
dist_transform = cv2.distanceTransform(opening, cv2.DIST_L2, 5)
# 作用:计算每个前景像素到最近背景像素的欧氏距离(L2范数)
# 参数5是距离变换的掩模大小(通常3~5,影响计算精度)
ret, sure_fg = cv2.threshold(dist_transform, 0.7 * dist_transform.max(), 255, cv2.THRESH_BINARY)
# 作用:保留距离背景较远的像素(硬币中心),阈值比例为0.7(经验值)
# 紧密粘连硬币可减小比例(如0.5),轻微粘连可增大比例(如0.8)
# 结果:二值图,白色(255)为确定的前景(硬币中心),黑色(0)为其他
# ===================== 6. 生成未知区域(背景 - 前景)=====================
sure_fg = np.uint8(sure_fg) # 转换为8位无符号整型(0-255)
unknown = cv2.subtract(sure_bg, sure_fg)
# 作用:未知区域 = 背景 - 前景(即硬币之间的边界或边缘像素)
# 这些区域是分水岭算法需要重点处理的部分
# ===================== 7. 标记生成(连通域标记 + 未知区域标记)=====================
ret, markers = cv2.connectedComponents(sure_fg)
# 作用:对确定的前景进行连通域分析,返回每个像素的连通域编号(背景为0,每个硬币为1,2,3...)
markers = markers + 1 # 标记值从1开始(避免0被误用,分水岭算法中0表示未知区域)
markers[unknown == 255] = 0 # 将未知区域标记为0(提示分水岭算法此处需计算边界)
# 最终:markers中,0=未知区域,1,2,3...=不同硬币的连通域
# ===================== 8. 执行分水岭分割 =====================
markers = cv2.watershed(img, markers)
# 作用:对输入图像img和标记图markers执行分水岭算法
# 算法会将未知区域(0)划分为不同连通域,并在分水岭边界处标记为-1
img[markers == -1] = [255, 255, 255] # 将分水岭边界(-1)在原图上标记为白色(可视化用)
# ===================== 9. 可视化各阶段结果 =====================
plt.figure(figsize=(8, 6))
# 子图1:开运算去噪后
plt.subplot(231)
plt.imshow(opening, cmap="gray")
plt.title("开运算去噪后")
plt.axis("off")
# 子图2:确定的背景区域
plt.subplot(232)
plt.imshow(sure_bg, cmap="gray")
plt.title("背景")
plt.axis("off")
# 子图3:确定的前景区域(硬币中心)
plt.subplot(233)
plt.imshow(sure_fg, cmap="gray")
plt.title("前景")
plt.axis("off")
# 子图4:未知区域(硬币边界)
plt.subplot(234)
plt.imshow(unknown, cmap="gray")
plt.title("未知区域")
plt.axis("off")
# 子图5:标记图(连通域+未知区域)
plt.subplot(235)
plt.imshow(markers, cmap="nipy_spectral") # 用光谱色显示不同标记值(连通域)
plt.title("标记图")
plt.axis("off")
# 子图6:最终分割结果(含分水岭边界)
plt.subplot(236)
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)) # BGR转RGB以正确显示颜色
plt.title("分割图(白色线为分水岭边界)")
plt.axis("off")
plt.tight_layout() # 自动调整子图间距
plt.show()
# 打印标记图的最小值(调试用,通常未知区域为0,连通域从1开始)
print("标记图最小值(未知区域):", markers.min())
print("标记图最大值(连通域):", markers.max()) # 输出标记图最大值(连通域)
unique_markers = np.unique(markers)
coin_count = len([m for m in unique_markers if m > 1]) # 假设1是背景
print("检测到的硬币数量:", coin_count)
