第八章 图像分割-part1
- 图像分割技术简介
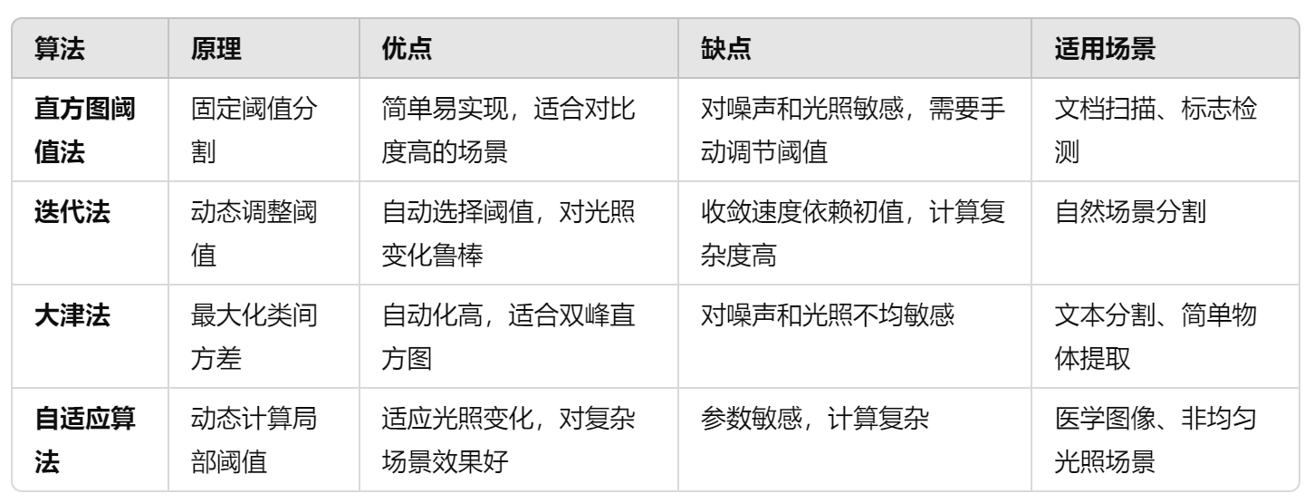
- 阈值分割
- 直方图阈值法
- 基本全局阈值法
- Otsu阈值法
- 移动平均阈值法
- 自适应阈值法
1. 图像分割算法
前言
图像分割就是将人们感兴趣的部分(前景)从背景中提取出来
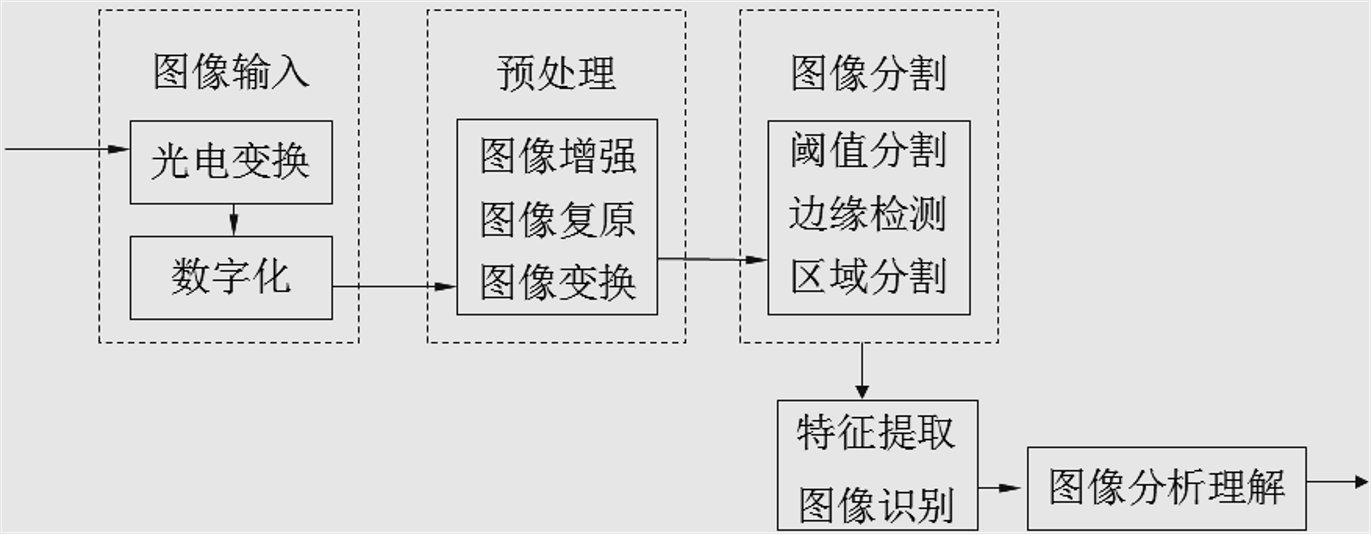
图像分割就是根据图像的 灰度、彩色、空间纹理、几何形状 等特征把图像划分成若干个互不相交的区域 ,使得这些特征在 同一区域内表现出一致性或相似性,而在 不同区域间表现出明显的不同。 如下图👇

随着深度学习技术的进步,图像分割技术也得到了很大的发展,目前已经出现了一些非常优秀的图像分割算法,基本的图像分割算法有:
- 灰度阈值分割
- 区域分割
- 边缘分割
还有更多的图像分割算法,如:🚀
- 基于聚类的分割
- 基于图论的分割
- 基于深度学习的分割
- 基于概率的分割
- 基于小波的分割
- 基于神经网络的分割
注意: 本节只介绍最基本的图像分割算法,其他的算法感兴趣的同学可以自行查阅相关资料。
2. 阈值分割
2.1 直方图阈值法
前言
在本学期前面是学过直方图的,这里简单回顾一下:
对于一幅灰度图像(像素值范围通常是0-255,0为纯黑,255为纯白),其灰度直方图是一个统计图表,横轴表示灰度级(0~255),纵轴表示该灰度级在图像中出现的像素数量(或频率)。

2. 直方图的直观意义
直方图的形状反映了图像中像素灰度的分布规律:
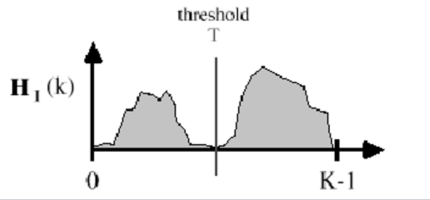
- 双峰直方图:图像中有明显的两类像素(如前景和背景),直方图会出现两个峰值(分别对应两类像素的灰度集中区域),两峰之间的谷底通常可以作为分割阈值。

- 单峰直方图:图像中像素灰度分布均匀(如渐变图像),难以直接通过阈值分割。
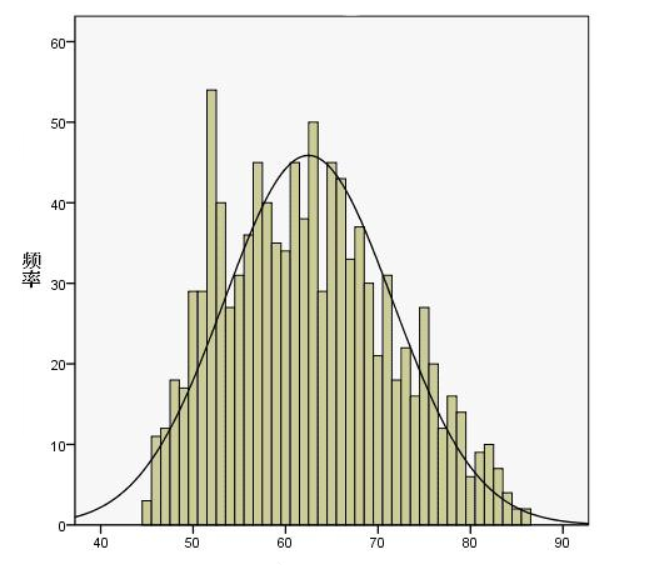
直方图阈值法的基本逻辑是:通过分析灰度直方图的分布,找到一个或多个阈值,将像素分为两类(如前景和背景),从而实现分割。
对于双峰直方图,可以找出两个峰值,分别对应前景和背景的灰度分布,然后取两个峰值的中间值作为阈值,将像素分为两类。公式如下:

对于三峰直方图,可以找出三个峰值,分别对应前景、背景和中间区域的灰度分布,然后取三个峰值的中间值作为阈值,将像素分为三类。公式如下:
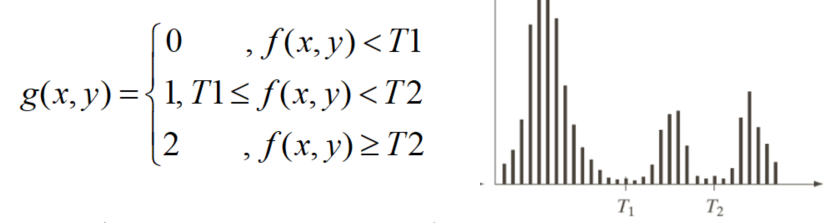
最大的问题是:如何确定阈值?
挑战:
- 噪声
- 不均匀光照
import numpy as np
import cv2
import matplotlib.pyplot as plt
import random
import math
%matplotlib inline
%config InlineBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
# 全局线性变换
def global_linear_transmation(im, c=0.0, d=255.0):
img = im.copy()
maxV = np.float32(img.max())
minV = np.float32(img.min())
for i in range(img.shape[0]):
for j in range(img.shape[1]):
img[i, j] = ((d-c) / (maxV - minV)) * (img[i, j] - minV) + c
return np.uint8(img)
# 添加椒盐噪声
def addSaltAndPepper(src, percentage):
NoiseImg = src.copy()
NoiseNum = int(percentage * src.shape[0] * src.shape[1])
for i in range(NoiseNum):
randX = random.randint(0, src.shape[0] - 1)
randY = random.randint(0, src.shape[1] - 1)
if random.randint(0, 1) == 0:
NoiseImg[randX, randY] = 0
else:
NoiseImg[randX, randY] = 255
return NoiseImg
# 添加高斯噪声
def addGaussianNoise(src, mu, sigma):
NoiseImg = src.copy()
NoiseImg = NoiseImg / NoiseImg.max()
rows = NoiseImg.shape[0]
cols = NoiseImg.shape[1]
for i in range(rows):
for j in range(cols):
NoiseImg[i,j] = NoiseImg[i,j] + random.gauss(mu, sigma)
maxV = NoiseImg.max()
minV = NoiseImg.min()
for i in range(NoiseImg.shape[0]):
for j in range(NoiseImg.shape[1]):
NoiseImg[i, j] = (1 / (maxV - minV)) * (NoiseImg[i, j] - minV)
img = np.uint8(NoiseImg * 255)
return img
# 添加瑞利噪声
def addRayleighNoise(src, scale):
NoiseImg = src.copy()
NoiseImg = NoiseImg / NoiseImg.max()
rows = NoiseImg.shape[0]
cols = NoiseImg.shape[1]
for i in range(rows):
for j in range(cols):
NoiseImg[i,j] = NoiseImg[i,j] + np.random.rayleigh(scale)
if NoiseImg[i,j] < 0:
NoiseImg[i,j] = 0
elif NoiseImg[i,j] > 1:
NoiseImg[i,j] = 1
NoiseImg = np.uint8(NoiseImg * 255)
return NoiseImg
# 添加不均匀光照效果
def addNonUniformIllumination(src):
# 创建渐变光照掩模(模拟从左上到右下的光照衰减)
rows, cols = src.shape
x = np.linspace(0, 1, cols)
y = np.linspace(0, 1, rows)
X, Y = np.meshgrid(x, y)
# 生成径向渐变(中心亮,四周暗)+ 方向性渐变(模拟斜向光源)
radial_gradient = 1 - np.sqrt((X - 0.5)**2 + (Y - 0.5)**2) * 0.8 # 径向衰减
directional_gradient = (X * 0.6 + Y * 0.4) # 方向性分量
# 组合渐变并归一化到0.6-1.0范围(模拟光照不均但不过于极端)
combined_gradient = (radial_gradient * 0.5 + directional_gradient * 0.5)
combined_gradient = np.clip(combined_gradient, 0.6, 1.0) # 限制范围
# 应用渐变到原图
illuminated = src.astype(np.float32) * combined_gradient
illuminated = np.clip(illuminated, 0, 255).astype(np.uint8)
return illuminated
plt.imshow(img_uneven, vmin=0, vmax=255, cmap='gray')
plt.title('不均匀光照')
plt.subplot(3, 4, 10)
img_uneven_flat = img_uneven.reshape(-1, 1)
countUneven, binsUneven, _ = plt.hist(img_uneven_flat, bins=128, color='brown', alpha=0.7)
if __name__ == '__main__':
# 读取图像(保持您原来的路径)
img = cv2.imread(r"./img/ch08-4(a).jpg", 0)
img0 = cv2.resize(img, (200, 150)) if img is not None else None
# 如果图像加载失败,创建模拟文档图像
if img0 is None:
print("图像加载失败,使用模拟文档图像演示")
img0 = np.ones((150, 200), dtype=np.uint8) * 200 # 浅灰背景
for i in range(20, 130, 25):
for j in range(30, 170, 30):
img0[i:i+8, j:j+4] = 50 # 暗色文字
img0 = cv2.resize(img0, (200, 150))
# 创建2行4列画布
plt.figure(figsize=(16, 8))
# ========== 第一行:原始图像及三种干扰图像 ==========
# 1. 原图
plt.subplot(2, 4, 1)
plt.axis("off")
plt.imshow(img0, cmap='gray', vmin=0, vmax=255)
plt.title('原始图像\n(模拟文档)')
# 2. 高斯噪声(方差0.05)
img_gauss = addGaussianNoise(img0.copy(), 0, 0.05)
plt.subplot(2, 4, 2)
plt.axis("off")
plt.imshow(img_gauss, cmap='gray', vmin=0, vmax=255)
plt.title('高斯噪声\n(σ=0.05)')
# 3. 椒盐噪声(5%)
img_sp = addSaltAndPepper(img0.copy(), 0.05)
plt.subplot(2, 4, 3)
plt.axis("off")
plt.imshow(img_sp, cmap='gray', vmin=0, vmax=255)
plt.title('椒盐噪声\n(5%)')
# 4. 不均匀光照
img_uneven2 = addNonUniformIllumination(img0.copy())
img_uneven = addGaussianNoise(img_uneven2, 0, 0.05)
plt.subplot(2, 4, 4)
plt.axis("off")
plt.imshow(img_uneven, cmap='gray', vmin=0, vmax=255)
plt.title('不均匀光照')
# ========== 第二行:对应直方图 ==========
# 5. 原图直方图
plt.subplot(2, 4, 5)
hist, bins = np.histogram(img0.flatten(), bins=128, range=[0,256])
plt.bar(bins[:-1], hist, width=1, color='black', alpha=0.7)
plt.title('原始直方图')
plt.xlim([0, 255])
# 6. 高斯噪声直方图
plt.subplot(2, 4, 6)
hist, bins = np.histogram(img_gauss.flatten(), bins=128, range=[0,256])
plt.bar(bins[:-1], hist, width=1, color='orange', alpha=0.7)
plt.title('高斯噪声直方图')
plt.xlim([0, 255])
# 7. 椒盐噪声直方图
plt.subplot(2, 4, 7)
hist, bins = np.histogram(img_sp.flatten(), bins=128, range=[0,256])
plt.bar(bins[:-1], hist, width=1, color='red', alpha=0.7)
plt.title('椒盐噪声直方图')
plt.xlim([0, 255])
# 8. 不均匀光照直方图
plt.subplot(2, 4, 8)
hist, bins = np.histogram(img_uneven.flatten(), bins=128, range=[0,256])
plt.bar(bins[:-1], hist, width=1, color='brown', alpha=0.7)
plt.title('不均匀光照直方图')
plt.xlim([0, 255])
plt.tight_layout()
plt.show()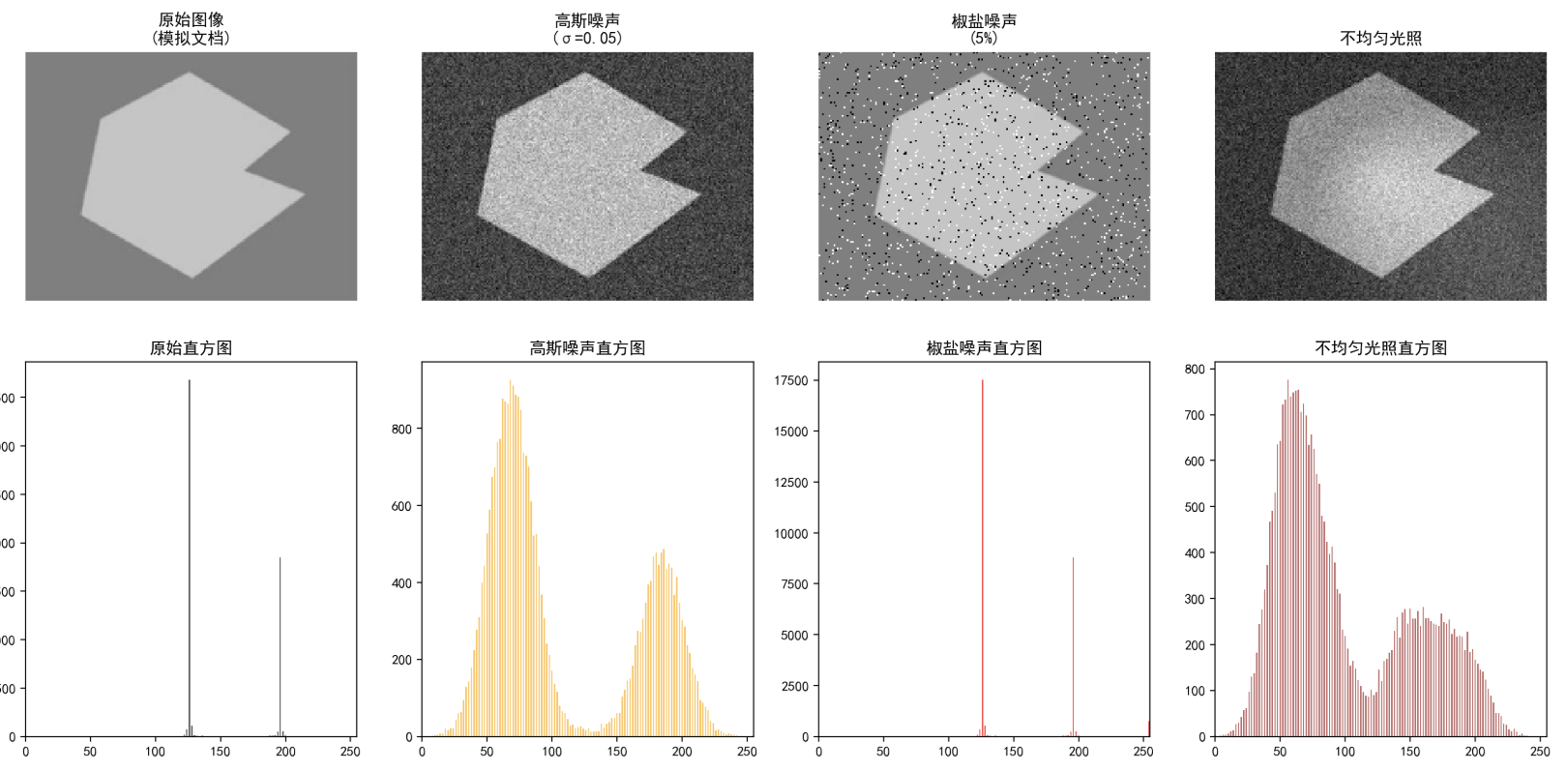
2.2 基本全局阈值法
前言
上一节我们介绍了直方图阈值法,但是它存在一个很大的问题:如何确定阈值?,这一节我们介绍一种基本的全局阈值法,它不需要手动设置阈值,而是通过计算得到一个最优的阈值。
1.定义
在图像分割任务中,若图像的目标(前景)和背景的灰度 差异明显 (例如文档中的黑白文字、显微镜下的细胞与背景),可以通过设定一个全局统一的阈值,将所有像素分为两类:
- 像素灰度值 ≥ 阈值 → 归为前景(或背景);
- 像素灰度值 < 阈值 → 归为背景(或前景)。
基本全局阈值法(Basic Global Thresholding) 是这类方法中最基础的算法,它通过迭代优化的方式,从图像整体出发自动确定一个“最佳” 的全局阈值,从而实现简单高效的分割。
2.核心逻辑
基本全局阈值法的核心逻辑是:先猜测一个初始阈值,用它分割图像并计算两类像素的平均灰度,再根据两类平均灰度更新阈值,不断迭代直到阈值稳定。最终得到的阈值能较好地区分前景和背景。
具体步骤:
步骤1:选个初始阈值
- 随便猜一个数字当阈值(比如直接用整张图片的平均灰度值,或者简单设成128)。
步骤2:按阈值分图片
用这个阈值把图片里的所有像素分成两类:
- 灰度值 比阈值小或等于 的像素 → 算成“背景类”;
- 灰度值 比阈值大 的像素 → 算成“目标类”。
步骤3:算两类的平均灰度
分别算出这两类像素自己的平均灰度值:
- “背景类”里所有像素灰度值的平均数;
- “目标类”里所有像素灰度值的平均数。
步骤4:更新阈值
把刚才算出来的两个平均灰度值 加起来再除以2,得到的新数字就是下一次要用的新阈值。
步骤5:检查是否停
看看新阈值和上一次用的阈值差别大不大(比如差值小于0.5或1这种很小的数):
- 如果差别很小 → 说明阈值已经稳定了,不用再改了,当前的阈值就是最后要用的最佳阈值;
- 如果差别还大 → 把新阈值当成当前的阈值,然后回到步骤2重新算,一直重复到阈值稳定为止。
总结:就是先猜一个阈值,分像素→算平均→调阈值,不断试直到阈值不再变,最后用这个稳定的值把图片分成目标和背景两部分。
案例代码和Otsu一起展示 👇
2.3 Otsu阈值法
前言
1.背景和定义
通过前面的学习,我们已经知道基本全局阈值法的核心是:先猜一个初始阈值,然后通过迭代计算两类像素的平均灰度,不断调整阈值直到稳定。这种方法虽然简单,但依赖初始值,且对前景和背景灰度分布重叠严重 的图像(比如直方图没有明显双峰)效果可能不佳——因为迭代过程只是机械地平衡两类均值,未必能找到真正让两类区分最明显的阈值。
那么,有没有一种方法能直接自动找到最优阈值,而且更科学地衡量“两类区分是否明显”呢?
答案就是本节要介绍的 Otsu阈值法(大津法),也叫最大类间方差法,它是图像处理领域最经典、最常用的自动阈值分割算法之一,核心思想是 “让前景和背景的差异最大化”,而非简单平衡两类均值。
2.Otsu阈值法的核心逻辑
- 分析直方图:先统计图像中每个灰度级(0~255)出现的频率(比如灰度值50的像素有多少个,灰度值100的像素有多少个)。
- 遍历所有可能的阈值:从灰度值0到255,依次假设每个灰度值作为候选阈值(比如先试试T=50,再试T=51,直到T=255)。
- 对每个阈值,把像素分成两类:
- 一类是灰度值 ≤ 阈值的像素(通常是背景);
- 另一类是灰度值 > 阈值的像素(通常是前景)。
- 计算每组阈值下的“类间方差”:衡量这两类像素的灰度差异有多大。
- 选方差最大的阈值 :当某个阈值对应的类间方差达到最大值时,说明用这个阈值分割后,前景和背景的区分最明显,这就是我们要找的最佳阈值!👍
补充: 👇
- 以最佳阈值将图像的灰度直方图分割成两部分,使两类之间的方差取最大值,即分离性最大。此算法利用了最小二乘法原理。
- 编程的时候可以使用穷尽法,让阈值T从0到L-1,找到方差最大的T值,即为最佳阈值。
3. 案例代码
import numpy as np
import cv2
from matplotlib import pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负
# 基本全局阈值法
def basic_global_thresholding(Img,T0=0.1): #输入的图像要求为灰度图像
'''
:param Img: 需进行全阈值分割的图像
:param T0: 迭代终止容差,当相临迭代得到的阈值差小于此值,则终止迭代
:return: 全阈值
'''
G1 = np.zeros(Img.shape, np.uint8) # 定义矩阵分别用来装被阈值T1分开的两部分
G2 = np.zeros(Img.shape, np.uint8)
T1 = np.mean(Img)
diff=255
while(diff>T0):
_,G1=cv2.threshold(Img,T1,255,cv2.THRESH_TOZERO_INV) #THRESH_TOZERO 超过thresh的像素不变, 其他设为0
_,G2=cv2.threshold(Img,T1,255,cv2.THRESH_TOZERO)
garray1 = np.array(G1)
garray2 = np.array(G2)
loc1 = np.where(garray1>0.001) #可以对二维数组操作
loc2 = np.where(garray2 > 0.001)
# g1 = list(filter(lambda a: a > 0, G1.flatten()))#只能对一维列表筛选,得到的是一个筛选对象
# g2 = list(filter(lambda a: a > 0, G2.flatten()))
ave1=np.mean(garray1[loc1])
ave2=np.mean(garray2[loc2])
T2=(ave1+ave2)/2.0
diff=abs(T2 - T1)
T1=T2
return T2
# 直方图
def histogram(image):
(row, col) = image.shape
#创建长度为256的list
hist = [0]*256
for i in range(row):
for j in range(col):
hist[image[i,j]] += 1
return hist
# 案例1
img = cv2.imread(r'./img/paopao.jpg',0)
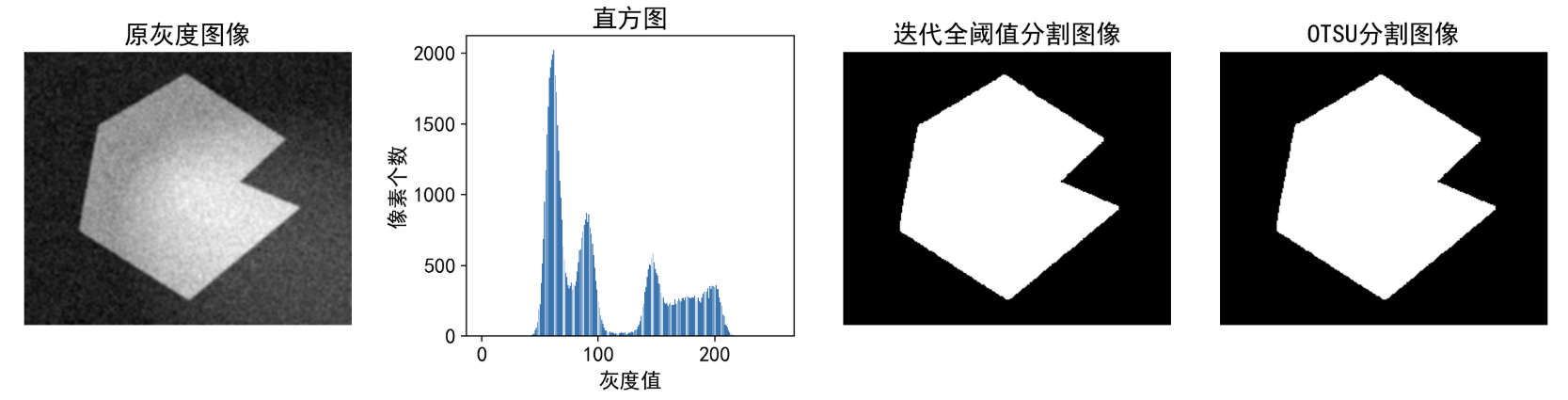
#案例2 将上面的注释 试试这个 叠加噪声和不均光照试试
# img22 = cv2.imread(r'./img/ch08-4(a).jpg',0) # 读取图像,0表示读取为灰度图像
# # 添加不均匀光照
# img_uneven222 = addNonUniformIllumination(img22.copy())
# # 添加高斯噪声
# img = addGaussianNoise(img_uneven222, 0, 0.05)
# #平滑一下
# img=cv2.blur(img,(3,3))
# 案例3 将上面的注释,试试这个
# img = cv2.imread(r'./img/ch11-01.png',0) # 读取图像,0表示读取为灰度图像
T2=basic_global_thresholding(img,T0=0.1) # 调用全局阈值分割函数,T0为迭代终止容差,当相临迭代得到的阈值差小于此值,则终止迭代
_,img_result=cv2.threshold(img,T2,255,cv2.THRESH_BINARY) # ,_为阈值,img_result为分割结果,255为最大值,THRESH_BINARY为二值化
_,img_otsu=cv2.threshold(img,128,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU) # Otsu阈值分割,128为初始阈值,255为最大值,THRESH_OTSU为Otsu阈值分割
plt.figure(figsize=(15,5))
plt.rcParams.update({"font.size":14})
plt.axes([0.0, 0.1, 0.2, 0.8])
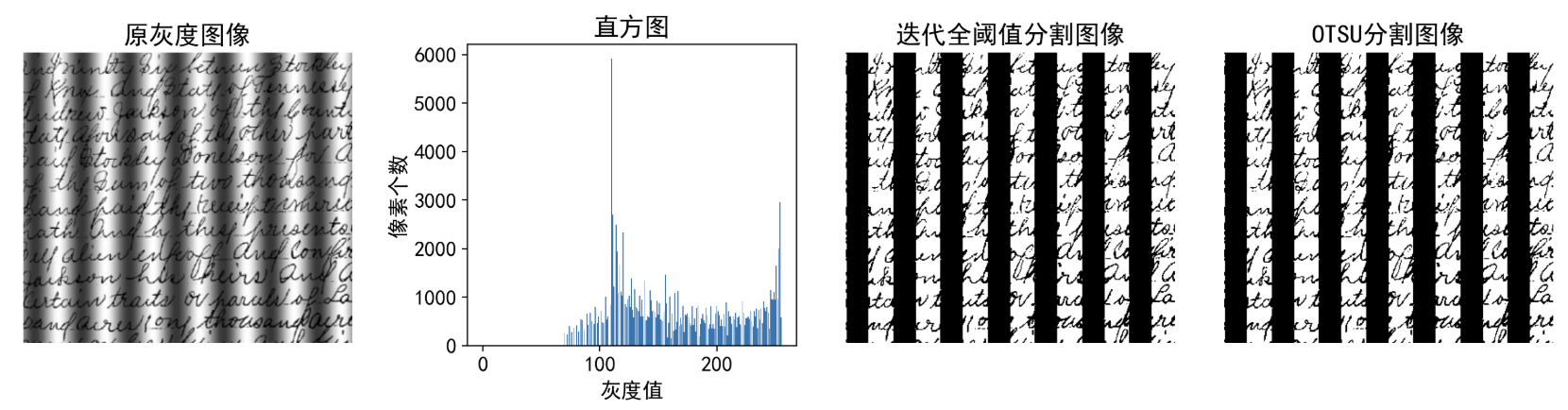
plt.title("原灰度图像")
plt.axis("off")
plt.imshow(img,cmap="gray")
plt.axes([0.27, 0.23, 0.2, 0.55])
plt.title("直方图")
h1=histogram(img)
plt.bar(range(256),h1)
plt.xlabel("灰度值")
plt.ylabel("像素个数")
plt.axes([0.5, 0.1, 0.2, 0.8])
plt.title("迭代全阈值分割图像")
plt.axis("off")
plt.imshow(img_result,cmap="gray")
plt.axes([0.73, 0.1, 0.2, 0.8])
plt.title("OTSU分割图像")
plt.axis("off")
plt.imshow(img_otsu,cmap="gray")
plt.show()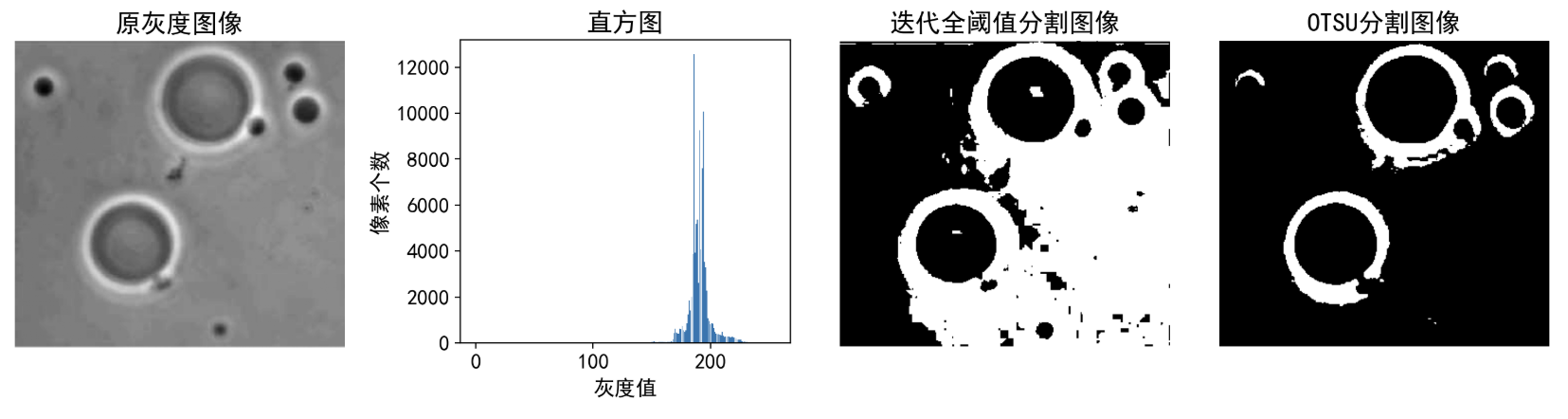
2.4 移动平均阈值法
前言
1.背景和定义
前面2种方法都是全局阈值法,它们的阈值是通过迭代计算得到的,但它们的计算过程是基于全局的,无法处理局部变化。
但在实际应用中,许多图像并不满足这些理想条件”,比如:👇
- 拍摄的文档可能存在光照不均(一侧亮、一侧暗)
- 工业检测中的零件可能因表面反光导致局部灰度突变
- 医学图像中器官与周围组织的灰度差异可能随区域变化。
这时,若用全局统一的阈值分割,会出现“某些区域分割准确,另一些区域却完全错误 ”的问题(例如:亮区文字被误判为背景,暗区背景被误判为目标)。
那么,有没有一种方法能根据图像不同区域的灰度特点,动态调整局部阈值,从而适应复杂光照或灰度变化的场景呢?
答案就是本节要介绍的 移动平均阈值法(Moving Average Thresholding) ,它是一种局部自适应阈值分割技术,核心思想是:通过滑动窗口计算局部区域的平均灰度,动态生成该区域的阈值,实现“哪里亮哪里调高阈值,哪里暗哪里调低阈值”的智能分割。
2.移动平均阈值法的核心逻辑 👇
- 划分局部区域 :把整张图片分成许多小的“窗口”(可以是固定大小的方块,比如15×15像素,也可以是滑动的窗口),每个窗口覆盖图像的一小部分。
- 计算局部平均灰度 :对每个小窗口内的所有像素,计算它们的灰度平均值(即该区域的“整体明暗程度”)。
- 动态生成局部阈值 :根据局部平均灰度,调整该窗口的阈值(例如:窗口较亮时,阈值适当提高,避免把亮背景误判为目标;窗口较暗时,阈值适当降低,避免把暗目标误判为背景)。
- 常见的调整方式 :直接用局部平均灰度作为阈值,或在其基础上加减一个固定偏移量(如阈值 = 局部平均灰度 ± 常数)。
- 逐区域分割 :对每个小窗口内的像素,用该窗口对应的局部阈值进行二值化(例如:像素灰度 ≥ 局部阈值 → 前景;像素灰度 < 局部阈值 → 背景)。
- 合并结果 : 将所有小窗口的分割结果拼接起来,形成整张图片的最终二值图像。
举个例子帮助理解
假设有一张扫描的文档图片,左侧因光源直射较亮(文字灰度约180200),右侧因阴影较暗(文字灰度约100120),背景左侧灰度约220240,右侧灰度约80100。

移动平均阈值法:将图片分成多个15×15的小窗口后,右侧亮区的窗口平均灰度约210,动态阈值可能设为200(文字180200仍高于阈值,被分为前景);左侧暗区的窗口平均灰度约90,动态阈值可能设为80(文字100120高于阈值,被分为前景)。最终,左右两侧的文字都能被准确分割,而背景被正确排除。

👇 👇
在OpenCV中,移动平均阈值法和自适应阈值法核心思想相似(都是局部自适应分割),但OpenCV官方库中没有直接提供“移动平均阈值法”的现成函数,而提供了专门的 cv2.adaptiveThreshold()函数来实现自适应阈值法。因此,两者的主要区别体现在:一个是需要手动实现(或自行封装逻辑),另一个是OpenCV原生支持。
2.5 自适应阈值法
前言
1.背景和定义
通过前面的学习,我们已经掌握了三种经典阈值分割方法:
- 基本全局阈值法(迭代平衡两类均值,适合简单均匀场景);
- Otsu阈值法(自动最大化类间方差,适合双峰直方图场景);
- 移动平均阈值法(通过局部窗口平均灰度动态调整阈值,应对光照不均)。
但在实际应用中,图像的复杂性可能远超想象:比如 👇
- 文档扫描时,不仅存在整体光照不均(左侧亮右侧暗),还可能因纸张褶皱、镜头畸变 导致局部区域的灰度突变(比如某个角落突然变暗或变亮);
- 医学图像中,器官与周围组织的灰度差异可能随位置微小变化而波动;
- 工业检测里,零件表面的反光点或划痕会让相邻像素的灰度值差异极大。
这时,“局部窗口平均灰度”的移动平均阈值法虽能适应一定程度的变化,但仍存在局限——它的阈值是基于固定大小的窗口内所有像素的平均值计算的,对窗口内的极端值(如突然出现的反光点)敏感 ,且窗口大小需要手动调整(太大则局部适应性差,太小则噪声多)。
那么,有没有一种方法能更精细地根据每个像素周围的局部灰度特征,动态计算专属阈值,从而实现对复杂场景中每一个微小区域的精准分割呢?
本节要介绍的 自适应阈值法 ,它是移动平均阈值法的升级版,核心思想是:为图像中的每个像素单独计算一个“量身定制”的阈值,该阈值由其周围邻近区域的灰度分布决定,实现真正的“因地制宜”分割。
2. 案例
在openCV中,可以用adaptiveThreshold()函数实现自适应阈值法,它有3个关键参数:
- src:待分割的灰度图像;
- maxValue:二值化后,像素值大于阈值时的最大值;
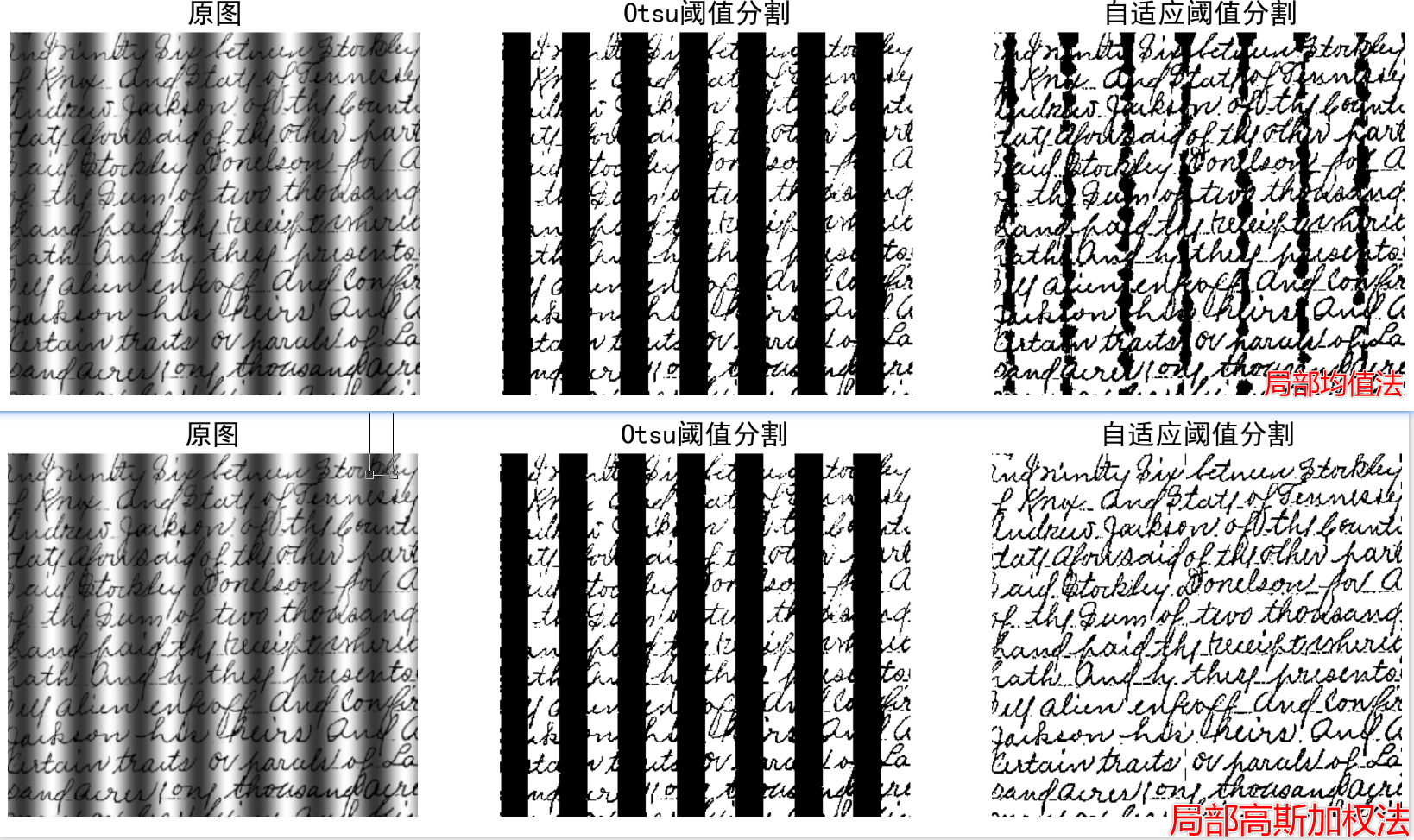
- adaptiveMethod:自适应阈值算法,可选ADAPTIVE_THRESH_MEAN_C(局部均值法)或ADAPTIVE_THRESH_GAUSSIAN_C(局部高斯加权法);
3. 案例代码
import numpy as np
import cv2
from matplotlib import pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负
img0 = cv2.imread(r'./img/light_circle.jpg',0)
# 案例2 将上面的注释,试试这个
img0 = cv2.imread(r'./img/ch11-01.png',0)
# 案例3 将上面的注释,试试这个
# img0 = cv2.imread(r'./img/Fig0926(a)(rice).tif',0)
_,img_seg=cv2.threshold(img0,128,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
# 自适应阈值分割 ADAPTIVE_THRESH_MEAN_C 为局部均值法,ADAPTIVE_THRESH_GAUSSIAN_C为局部高斯加权法,THRESH_BINARY为二值化,kernalSize为窗口大小,6为偏移量
kernalSize=19
img_seg_adapt = cv2.adaptiveThreshold(img0, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, kernalSize, 6)
# 自适应阈值分割 ADAPTIVE_THRESH_MEAN_C 为局部均值法,ADAPTIVE_THRESH_GAUSSIAN_C为局部高斯加权法,THRESH_BINARY为二值化,kernalSize为窗口大小,6为偏移量
plt.figure(figsize=(15,5))
plt.subplot(131)
plt.imshow(img0,cmap="gray")
plt.axis("off")
plt.title("原图")
plt.subplot(132)
plt.imshow(img_seg,cmap="gray")
plt.axis("off")
plt.title("Otsu阈值分割")
plt.subplot(133)
plt.imshow(img_seg_adapt,cmap="gray")
plt.axis("off")
plt.title("自适应阈值分割")
plt.show()

总结