第五章 图像复原
大约 8 分钟数字图像处理数字图像处理
完成227页的实验四内容
图像复原实验
1.实验目的
- 理解图像复原的基本原理和方法
- 理解图像复原的算法及其性能
2.实验内容
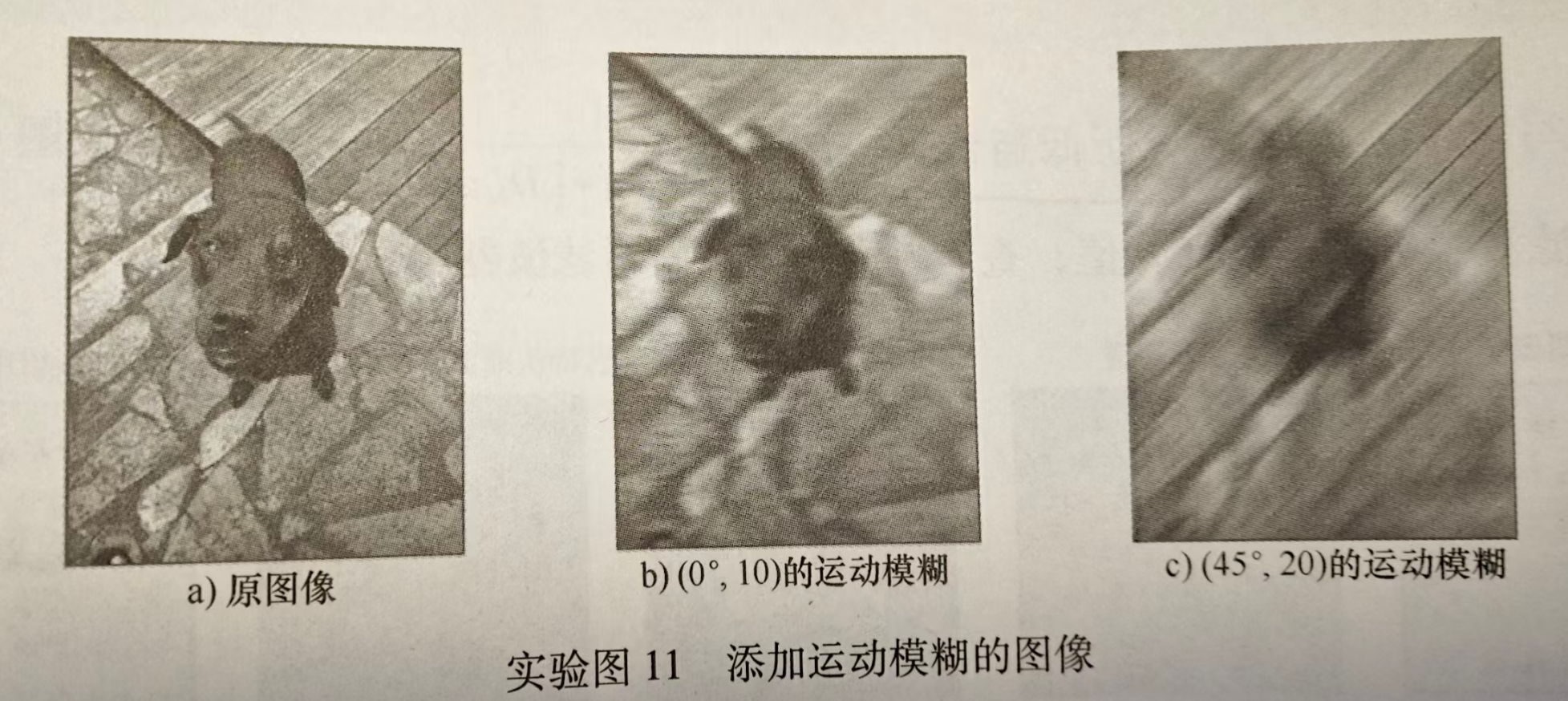
1. 完善以下程序,实现在空域给图像添加指定方向、大小的运动模糊,效果如实验图11所示。其中,实验图11b添加了方向为0°、强度为10 的运动模糊;实验图 11c 添加了方向为 45°、强度为 20 的运动模糊。
完成下列代码填空👇
import numpy as np
import cv2
#生成运动模糊核
def make_PSF(kernel_size=15, angle=60):
PSF = np.diag(np.ones(kernel_size)) #初始模糊核的方向是-45°
angle = angle + 45 #抵消-45°的影响
M = cv2.getRotationMatrix2D((kernel_size/2, kernel_size/2), angle, 1) #生成旋转算子
PSF = cv2.warpAffine(这里怎么填啊) #实现旋转变换
PSF = PSF / PSF.sum() #使模糊核的权重和为1
return PSF
#在空域对图像进行运动模糊
def motion_blur(image, PSF):
blurred = 这里怎么填啊 #通过二维卷积运算给图像添加模糊
#convert to uint8
cv2.normalize(blurred, blurred, 0, 255, cv2.NORM_MINMAX)
blurred = np.array(blurred, dtype=np.uint8)
return blurred
if __name__ == "__main__":
img = cv2.imread('./img/adip.png', 0) # 以灰度模式读取图像
PSF = 这里怎么填啊()
img_ = 这里怎么填啊(img, PSF)
cv2.imshow('Source image', img)
cv2.imshow('blur image', img_)
cv2.waitKey(0)
cv2.destroyAllWindows()2. 阅读并完善以下程序,要求先给图像添加强度为15,方向为60°的运动模糊,然后使用逆滤波进行图像复原,效果如实验图12所示。

完成下列代码填空👇
import matplotlib.pyplot as plt
import numpy as np
from numpy import fft
from __future__ import division # 在此需要调用第1题的make_PSF函数
import math
import cv2
# 此函数扩展运动模糊PSF,使之与原图像image0具有同样的维度大小
def extension_PSF(image0, PSF0):
[img_h, img_w] = image0.shape
[h, w] = PSF0.shape # 获取运动模糊核的维度
PSF = np.zeros((img_h, img_w)) # 初始化扩展后的运动模糊核
PSF[0:h, 0:w] = 这里填什么
return PSF
# 在频域对图像进行运动模糊
def make_blurred(input, PSF, eps):
input_fft = 这里填什么 # 对输入图像进行傅里叶变换
# 对运动模糊核进行傅里叶变换,并加上一个很小的数
PSF_fft = fft.fft2(PSF) + eps
blurred = fft.ifft2( 这里填什么 ) # 在频域进行运动模糊
blurred = np.abs(blurred)
return blurred
def inverse(input, PSF, eps): # 逆滤波
input_fft =这里填什么 # 对退化图像进行傅里叶变换
# 对运动模糊核进行傅里叶变换,并加上一个很小的数
PSF_fft = 这里填什么
Output_fft = 这里填什么 # 在频域进行逆滤波
result = fft.ifft2(Output_fft) # 进行傅里叶反变换
result = np.abs(result)
return result
if __name__ == "__main__": # 主程序判断语句
image = cv2.imread('这里填什么', 0) # 以灰度模式读取图像
plt.figure(figsize=(8, 6))
plt.subplot(131)
plt.axis("off")
plt.title("Original Image")
plt.gray()
plt.imshow(image) # 显示原图像
# 生成运动模糊核
PSF = 这里填什么 # 这里简单创建一个15x15的零矩阵作为示例,实际应根据需求生成
PSF[7, :] = 1 # 假设水平方向的运动模糊
PSF = PSF / np.sum(PSF) # 归一化
# 扩展PSF,使其与图像一样大小
PSF = 这里填什么
blurred = make_blurred(image, PSF, 1e-6) # 在频域对图像进行运动模糊
plt.subplot(132)
plt.axis("off")
plt.title("Motion blurred")
plt.imshow(blurred)
result = inverse(blurred, PSF, 1e-6) # 逆滤波
plt.subplot(133)
plt.axis("off")
plt.title("inverse deblurred")
plt.imshow(result)
plt.show()3.阅读并完善以下程序,首先给运动模糊图像添加噪声,然后分别用逆滤波和维纳滤波进行图像复原,效果如实验图13所示,最后分析K值对维纳滤波器影响。
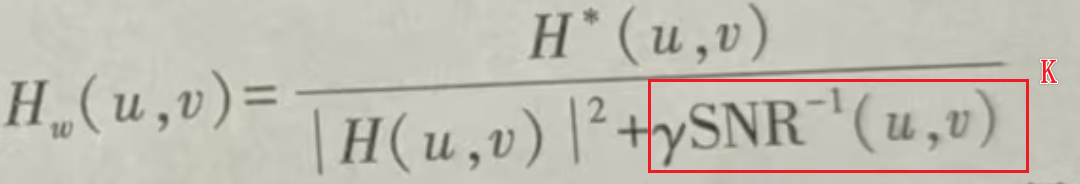

完成下列代码填空👇
# 维纳滤波图像复原(wienerNoise.py)
import cv2
import numpy as np
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
# 生成运动模糊核PSF
def make_PSF(kernel_size=15, angle=60):
"""
生成运动模糊点扩散函数(PSF)
参数:
kernel_size: 模糊核大小
angle: 运动方向角度(度)
返回:
PSF: 归一化的运动模糊核
"""
PSF = np.diag(np.ones(kernel_size)) # 初始模糊核的方向是-45度(对角线)
angle = angle + 45 # 抵消-45度的影响,使角度参数直观
# 图像旋转是一种几何变换,实现图像几何变换有两步:先生成变换算子,再执行变换
M = cv2.getRotationMatrix2D((kernel_size / 2, kernel_size / 2), angle, 1) # 生成旋转算子
PSF = cv2.warpAffine(PSF, M, (kernel_size, kernel_size), flags=cv2.INTER_LINEAR)
PSF = PSF / PSF.sum() # 模糊核的权重和为1
return PSF
# 此函数扩展运动模糊核PSF0,使之与原图像image0一样大小
def extension_PSF(image0, PSF0):
[img_h, img_w] = image0.shape
[h, w] = PSF0.shape
PSF = np.zeros((img_h, img_w))
PSF[0:h, 0:w] = PSF0
return PSF
# 在频域对图片进行模糊
def make_blurred(input, PSF):
"""
在频域进行图像模糊处理
参数:
input: 输入图像
PSF: 点扩散函数
返回:
blurred: 模糊后的图像
"""
input_fft = 这里填什么? # 进行二维数组的傅里叶变换
PSF_fft = np.fft.fft2(PSF)
blurred = np.fft.ifft2(这里填什么?) # 频域卷积等于空间域卷积
blurred = np.abs(blurred)
return blurred
def inverse_filter(input, PSF, eps=1e-6):
input_fft = 这里填什么?
PSF_fft = 这里填什么?
result = np.fft.ifft2(input_fft / (PSF_fft + eps))
result = np.abs(result)
return result
def wiener(input, PSF, K=1e-3):
"""
维纳滤波图像复原
参数:
input: 模糊图像
PSF: 点扩散函数
K: 噪声功率与信号功率之比(正则化参数)
返回:
result: 复原后的图像
"""
input_fft = np.fft.fft2(input)
PSF_fft = np.fft.fft2(PSF)
# 维纳滤波公式:H*/(|H|² + K)
PSF_fft_1 = np.conj(PSF_fft) / (np.abs(PSF_fft) ** 2 + K)
result = 这里填什么?
result = np.abs(result)
return result
if __name__ == "__main__":
# 读取并预处理图像
image = cv2.imread('这里填什么?',0) # 请确保路径正确
# 生成运动模糊核
PSF = make_PSF(33, -60)
# 扩展PSF使其与图像大小一致
PSF = extension_PSF(image, PSF)
# 1. 原始图像
plt.figure(figsize=(12, 8))
plt.subplot(221)
plt.axis("off")
plt.gray()
plt.title("原图")
plt.imshow(image)
# 2. 运动模糊+噪声图像
# 在频域对图片进行运动模糊
blurred = np.abs(make_blurred(image, PSF))
# blurred_noisy = cv2.filter2D(image, -1,PSF)
blurred_noisy = blurred + 0.1 * blurred.std() * np.random.standard_normal(blurred.shape)
plt.subplot(222)
plt.axis("off")
plt.gray()
plt.title("模糊噪声图")
plt.imshow(blurred_noisy)
# 3. 逆滤波复原
inverse_result = inverse_filter(blurred_noisy, PSF, eps=1e-6)
plt.subplot(223)
plt.axis("off")
plt.gray()
plt.title("逆滤波")
plt.imshow(inverse_result)
# 4. 维纳滤波复原
wiener_result = 这里填什么?
plt.subplot(224)
plt.axis("off")
plt.gray()
plt.title("维纳(K=0.01)")
plt.imshow(wiener_result)
plt.tight_layout()
plt.show()
4.程序填空,使用均方误差来评价维纳滤波的图像复原效果,分析维纳滤波器的K值对图像复原的影响。
完成下列代码填空👇
import cv2
import numpy as np
from matplotlib import pyplot as plt
# 计算两图像的均方误差
def meanSquare(image0, image1):
[m, n] = image0.shape
MSE = 0
for i in range(m):
for j in range(n):
MSE = 这里填什么? # 按公式计算误差累加和
MSE = MSE / (m * n)
return MSE
if __name__ == "__main__":
image = cv2.imread('./img/kennysmall.jpg')
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
PSF = make_PSF()
PSF = extension_PSF(image, PSF)
blurred = make_blurred(image, PSF)
# 添加噪声, standard_normal 产生随机的函数
blurred_noisy = blurred + 0.5 * blurred.std() * np.random.standard_normal(blurred.shape)
K = 0.005
MSE_min = np.inf
best_K_list = [] # 用于存储每次的最佳K值,便于后续分析
best_restruct = None
while K < 0.5:
restruct = 这里填什么? # 对添加噪声的图像进行维纳滤波
MSE = meanSquare(restruct, image) # 计算重构图像与原始图像之间的均方误差
if MSE < MSE_min:
K_best = K
MSE_min = MSE
best_K_list.append(K_best) # 存储本次最佳K值
best_restruct=restruct
print('MSE:',MSE)
K = 这里填什么? # 更新K值,步长可以根据需要调整
print('The best K is', K_best)
plt.figure(figsize=(10, 5))
# 原图
plt.subplot(1, 3, 1)
plt.imshow(image, cmap='gray')
plt.axis('off')
plt.title('原图(清晰图像)')
# 模糊+噪声图像
plt.subplot(1, 3, 2)
plt.imshow(blurred_noisy, cmap='gray')
plt.axis('off')
plt.title('模糊+噪声图像')
# 维纳滤波复原图(使用最佳K值)
plt.subplot(1, 3, 3)
plt.imshow(best_restruct, cmap='gray')
plt.axis('off')
plt.title(f'维纳滤波复原图\n(K={K_best:.3f})')
plt.tight_layout()
plt.show()
