第五章 图像复原
1. 图像复原算法
图像复原算法
一、图像复原就像修复老照片
想象你有一张祖传的老照片,已经泛黄模糊,还带着划痕。图像复原技术就像一位专业的照片修复师,只不过用的是数学方法而不是画笔。

典型场景:
- 模糊的监控录像要看清车牌
- 医学影像需要更清晰诊断
- 天文照片要去除大气干扰
- 手机拍糊的照片想挽救

二、无约束复原:简单粗暴的"时光倒流"
1️⃣ 1. 逆滤波——最直接的思路
就像你知道照片是因为镜头晃动变模糊的,于是尝试"倒着晃动"来还原。数学上就是直接除以模糊函数。
**简单的比喻:**逆滤波就像一个人拼命想擦干净一块脏玻璃(去模糊),结果用力过猛,把抹布上的脏东西(噪声)全糊在玻璃上了,越擦越花。
适合情况:
- 非常清楚模糊原因(比如知道相机抖动了多少像素)
- 图片几乎没有噪点(像在无尘室拍的照片)

致命缺点:
- ⚠️对噪声极度敏感,就像用放大镜看老照片时,连灰尘颗粒都被放大了⚠️
- 遇到某些频率会除零出错
2️⃣ 2. 伪逆滤波——给方法装上安全阀
在逆滤波基础上加了个" 保险丝 ",当发现要 除以接近零 的数时就停止操作。
就像修照片时,发现某块区域信息完全丢失了,就不再强行修复。
实际应用:
- 卫星图片去模糊(知道卫星抖动特性)
- 显微镜图像校正(了解镜头畸变参数)
镜头畸变是指光学透镜在成像时产生的几何形变
三、有约束复原:更聪明的修复策略
3️⃣ 3. 维纳滤波——懂平衡的艺术
就像经验丰富的修图师,既要去模糊又要控制噪声。它会自动权衡:
- 高频部分(细节)保留多少
- 噪声要抑制到什么程度
公式: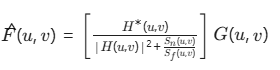
H(u,v):模糊函数(知道镜头怎么模糊的)- 例如:相机抖动模糊的轨迹
*H(u,v):H的复共轭(数学上表示反向操作)- 相当于:"既然模糊是往右抖,那我就往左抖回去"
- 分母部分:关键创新点
|H|²:模糊程度的强度Sn/Sf:噪声功率谱/信号功率谱(信噪比的倒数)- 作用:当信噪比低时(Sn大),公式自动减小修复力度,防止放大噪声
就像修复师工作时:
- 发现图片某区域信噪比高(如蓝天):大胆修复细节
- 发现信噪比低(如阴影部分):保守处理避免噪点

典型用途:
- 老电影修复(同时处理划痕和模糊)
- CT扫描图像(在低辐射剂量下保持清晰)
4️⃣4. 约束最小二乘(维纳滤波变种)——自带保护机制的修复
“二乘/平方”的思想:“复原后的图像再经过模糊”与“你手中已有的模糊图像”之间的差距
相当于在修复时给自己定规矩:
- 修复后的图像要尽可能接近模糊前的样子
- 同时要保持图像自然(不过度锐化)
一句话概括核心思想:“带着刹车去还原图像”,在追求清晰度的同时,用一个“平滑”的约束管住自己,防止把噪声也一并放大了,从而得到一个既清晰又干净的结果。
公式: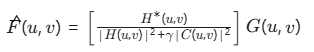
公式说明:
C(u,v):约束算子(通常用拉普拉斯算子)- 物理意义:惩罚图像中不自然的高频突变
- 效果类似:"修复后相邻像素亮度不要跳变太大"
γ:调节参数γ=0:退化成逆滤波(完全不管噪声)γ→∞:图像过度平滑(像打了马赛克)

关键改进 :
不需要知道噪声统计量(Sn/Sf),而是通过:
- 约束图像的二阶微分能量(|C(u,v)|²)
- 用γ平衡"去模糊"和"平滑度"
就像考古修复文物 :
γ是"保守程度"旋钮:
- 调小:大胆还原纹饰(可能引入伪影)
- 调大:优先保证完整性(可能丢失细节)实际选择口诀:
- 知道怎么模糊的 + 几乎没噪声 → 逆滤波
- 知道怎么模糊的 + 有点噪声 → 伪逆滤波
- 知道怎么模糊的 + 知道噪声水平 → 维纳滤波
- 知道怎么模糊的 + 不知道噪声 → 约束最小二乘
- 不知道怎么模糊的 → 需要更高级的盲去卷积
工程选择建议:
- 优先尝试维纳滤波如果:
- 有噪声统计数据(如相机ISO噪声模型)
- 处理同类批量图像(如医学影像序列)
- 优先约束最小二乘如果:
- 噪声特性复杂(如扫描的古籍)
- 需要灵活调节结果(交互式修复系统)
- 高级技巧:
- 维纳滤波的K=Sn/Sf可以分区设置(天空用大K,建筑用小K)
- 约束最小二乘的C算子可以定制(如针对文字图像优化)
案例代码:
import numpy as np
import math
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format="retina" # 修复了这里的拼写错误
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
# 生成大气湍流模糊核
def turbulence_PSF(input, k):
"""
生成大气湍流点扩散函数(PSF)
参数:
input: 输入图像,用于获取尺寸
k: 湍流强度参数,k越大模糊越强
返回:
PSF1: 归一化的大气湍流模糊核
"""
[m, n] = input.shape
PSF = np.zeros((m, n))
p = m / 2 # 中心点坐标
q = n / 2
# 生成基于距离的湍流模糊核
for u in range(m):
for v in range(n):
PSF[u, v] = math.exp(-k * ((u-p)*(u-p) + (v-q)*(v-q))**(5/6))
PSF1 = np.fft.ifft2(PSF) # 逆傅里叶变换得到空间域模糊核
PSF1 = np.abs(PSF1)
PSF1 = PSF1 / PSF1.sum() # 模糊核的权重和为1
return PSF1
# 此函数生成的运动模糊核是由旋转来控制运动方向
def make_PSF(kernel_size=15, angle=60):
"""
生成运动模糊点扩散函数(PSF)
参数:
kernel_size: 模糊核大小
angle: 运动方向角度(度)
返回:
PSF: 归一化的运动模糊核
"""
PSF = np.diag(np.ones(kernel_size)) # 初始模糊核的方向是-45度(对角线)
angle = angle + 45 # 抵消-45度的影响,使角度参数直观
# 图像旋转是一种几何变换,实现图像几何变换有两步:先生成变换算子,再执行变换
M = cv2.getRotationMatrix2D((kernel_size / 2, kernel_size / 2), angle, 1) # 生成旋转算子
PSF = cv2.warpAffine(PSF, M, (kernel_size, kernel_size), flags=cv2.INTER_LINEAR)
PSF = PSF / PSF.sum() # 模糊核的权重和为1
return PSF
# 此函数扩展PSF0,使之与image0一样大小
def extension_PSF(image0, PSF0):
"""
将小尺寸的PSF扩展到与图像相同尺寸
参数:
image0: 原始图像
PSF0: 小尺寸模糊核
返回:
PSF: 扩展后的模糊核
"""
[img_h, img_w] = image0.shape
[h, w] = PSF0.shape
PSF = np.zeros((img_h, img_w))
PSF[0:h, 0:w] = PSF0[0:h, 0:w] # 将小模糊核放在大矩阵的左上角
return PSF
# 在频域对图片进行模糊
def make_blurred(input, PSF):
"""
在频域进行图像模糊处理
参数:
input: 输入图像
PSF: 点扩散函数
返回:
blurred: 模糊后的图像
"""
input_fft = np.fft.fft2(input) # 进行二维数组的傅里叶变换
PSF_fft = np.fft.fft2(PSF)
blurred = np.fft.ifft2(input_fft * PSF_fft) # 频域卷积等于空间域卷积
blurred = np.abs(blurred)
return blurred
def inverse(input, PSF):
"""
逆滤波图像复原
参数:
input: 模糊图像
PSF: 点扩散函数
返回:
result: 复原后的图像
"""
input_fft = np.fft.fft2(input)
PSF_fft = np.fft.fft2(PSF) + 1e-3 # 为了避免分母为零,将PSF的傅里叶变换加一个极小值eps
result = np.fft.ifft2(input_fft / PSF_fft) # 逆滤波公式
result = np.abs(result)
return result.copy()
# 伪逆滤波
def Pseudo_inverse(input, PSF, w, k):
"""
伪逆滤波图像复原
参数:
input: 模糊图像
PSF: 点扩散函数
w: 截止频率半径
k: 高频增强系数
返回:
result: 复原后的图像
"""
input_fft = np.fft.fft2(input)
input_sfft = np.fft.fftshift(input_fft) # 将零频率移到中心
PSF_fft = np.fft.fft2(PSF)
PSF_sfft = np.fft.fftshift(PSF_fft)
[M, N] = input_fft.shape
c0 = int((M-1)/2) # 频率域中心坐标
c1 = int((N-1)/2)
F = np.zeros((M, N)) + 0j # 创建复数数组
# 在频率域进行滤波处理
for u in range(M):
for v in range(N):
D = np.sqrt((u-c0)**2 + (v-c1)**2) # 计算到频率域中心的距离
if D <= w: # 低频区域使用逆滤波
F[u, v] = input_sfft[u, v] / PSF_sfft[u, v]
else: # 高频区域使用直接传递(避免噪声放大)
F[u, v] = k * input_sfft[u, v]
result = np.fft.ifft2(np.fft.fftshift(F)) # 移回原始频率布局并逆变换
return np.abs(result)
def wiener(input, PSF, K=1e-3):
"""
维纳滤波图像复原
参数:
input: 模糊图像
PSF: 点扩散函数
K: 噪声功率与信号功率之比(正则化参数)
返回:
result: 复原后的图像
"""
input_fft = np.fft.fft2(input)
PSF_fft = np.fft.fft2(PSF)
# 维纳滤波公式:H*/(|H|² + K)
PSF_fft_1 = np.conj(PSF_fft) / (np.abs(PSF_fft) ** 2 + K)
result = np.fft.ifft2(input_fft * PSF_fft_1)
result = np.abs(result)
return result
def clsFilter(image, PSF, Q, lambd=1e-3):
"""
约束最小二乘滤波图像复原
参数:
image: 模糊图像
PSF: 点扩散函数
Q: 约束算子(通常是拉普拉斯算子)
lambd: 正则化参数
返回:
result: 复原后的图像
"""
input_fft = np.fft.fft2(image)
PSF_fft = np.fft.fft2(PSF)
Q_fft = np.fft.fft2(Q)
# 约束最小二乘滤波公式:H*/(|H|² + λ|Q|²)
PSF_fft_1 = np.conj(PSF_fft) / (np.abs(PSF_fft) ** 2 + lambd * np.abs(Q_fft) ** 2)
result = np.fft.ifft2(input_fft * PSF_fft_1)
result = np.abs(result)
return result
# 主程序开始
# 读取图像
image = cv2.imread('./img/adip.png', 0) # 以灰度模式读取图像
# 生成运动模糊核并扩展
PSF0 = make_PSF(20, -60) # 生成20x20大小,角度为-60度的运动模糊核
PSF = extension_PSF(image, PSF0) # 扩展psf,使其大小与图像大小一致
# 在频域对图片进行运动模糊
blurred = np.abs(make_blurred(image, PSF))
# 产生最小二乘滤波需要的锐化算子(拉普拉斯算子)
lap0 = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]]) # 拉普拉斯算子模板
# 扩展到图像尺寸,如下:
# [0,1,0]
# [1,-4,1]
# [0,1,0]
lap = extension_PSF(image, lap0) # 扩展到图像尺寸,如下:
# [[ 0. 1. 0. ... 0. 0. 0.]
# [ 1. -4. 1. ... 0. 0. 0.]
# [ 0. 1. 0. ... 0. 0. 0.]
# ...
# [ 0. 0. 0. ... 0. 0. 0.]
# [ 0. 0. 0. ... 0. 0. 0.]
# [ 0. 0. 0. ... 0. 0. 0.]]
# 创建显示窗口
fig, axes = plt.subplots(3, 4, sharex=True, sharey=True, figsize=(14, 10))
# 设置不同噪声水平进行测试
w = 0.5 # 初始噪声强度
noise_levels = ['高噪声', '中噪声', '低噪声'] # 噪声水平标签
for i in range(3):
# 添加不同强度的噪声
blurred_noisy = blurred + w * blurred.std() * np.random.standard_normal(blurred.shape)
#blurred_noisy是模糊+噪声图像,PSF是运动模糊核
# 使用不同方法进行图像复原
imgRI = inverse(blurred_noisy, PSF) # 逆滤波,blurred_noisy是模糊+噪声图像,PSF是运动模糊核
imgRW = wiener(blurred_noisy, PSF, w/10) # 维纳滤波,w/10是噪声强度,w/10越小,噪声越小,复原效果越好
imgRC = clsFilter(blurred_noisy, PSF, lap, w/10) # 约束最小二乘滤波,w/10是噪声强度,w/10越小,噪声越小,复原效果越好 lap是拉普拉斯算子
# 显示结果
axes[i, 0].imshow(blurred_noisy, cmap="gray")
axes[i, 0].set_title(f'模糊+噪声\n({noise_levels[i]})', fontsize=10)
axes[i, 0].set_xticks([]), axes[i, 0].set_yticks([])
axes[i, 1].imshow(imgRI, cmap="gray")
axes[i, 1].set_title('逆滤波复原', fontsize=10)
axes[i, 1].set_xticks([]), axes[i, 1].set_yticks([])
axes[i, 2].imshow(imgRW, cmap="gray")
axes[i, 2].set_title('维纳滤波复原', fontsize=10)
axes[i, 2].set_xticks([]), axes[i, 2].set_yticks([])
axes[i, 3].imshow(imgRC, cmap="gray")
axes[i, 3].set_title('约束最小二乘复原', fontsize=10)
axes[i, 3].set_xticks([]), axes[i, 3].set_yticks([])
w /= 10 # 降低噪声强度
plt.subplots_adjust(wspace=0.05, hspace=0.15) # 调整子图间距
plt.suptitle('不同噪声水平下的图像复原方法比较', fontsize=14, fontweight='bold')
plt.show()
结果分析: 👇
- 第一行(高噪声情况):
- 逆滤波:效果最差,噪声被严重放大
- 维纳滤波:有一定去噪效果,但细节损失较多
- 约束最小二乘:平衡了去模糊和去噪,效果相对较好
- 第二行(中噪声情况):
- 所有方法效果都有所改善
- 逆滤波开始显现一些复原效果,但仍有噪声
- 维纳滤波和约束最小二乘效果接近
- 第三行(低噪声情况):
- 逆滤波效果最佳(接近理论最优)
- 维纳滤波和约束最小二乘也表现良好
- 方法比较结论:
- 噪声水平高时:约束最小二乘 > 维纳滤波 > 逆滤波
- 噪声水平低时:逆滤波 ≈ 约束最小二乘 ≈ 维纳滤波
总结:
- 逆滤波 :
- 优点:理论简单,无噪声时效果最好
- 缺点:对噪声敏感,高频噪声会被放大
- 适用场景:噪声极小的理想情况
- 维纳滤波:
- 优点:考虑了噪声统计特性,抗噪性好
- 缺点:需要估计噪声功率谱
- 适用场景:已知或可估计噪声特性的情况
- 约束最小二乘滤波:
- 优点:引入平滑约束,能有效抑制噪声
- 缺点:需要选择合适的约束算子
- 适用场景:需要平衡去模糊和去噪的情况
2. 案例:图像复原
前言
实验设计说明
三种退化情况:
-45度平面匀速运动模糊
- 只添加运动模糊,无噪声
- 测试理想情况下各方法的性能
- 大气湍流模糊 + 高斯噪声
- 模拟大气扰动造成的模糊
- 添加适量高斯噪声
- 测试方法对复杂模糊和噪声的适应性
- 120度平面匀速运动模糊 + 高斯噪声
- 不同角度的运动模糊
- 添加高斯噪声
- 测试方法对不同方向模糊的鲁棒性
复原方法对比:
- 逆滤波
- 维纳滤波
- 约束最小二乘
import numpy as np
import math
import cv2
import matplotlib.pyplot as plt
from scipy import ndimage
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 生成大气湍流模糊核, 原理是高斯函数的5/3次方,模拟大气湍流的模糊效果
def turbulence_PSF(img_size, k=0.0025):
m, n = img_size
PSF = np.zeros((m, n))
center_x, center_y = n//2, m//2
for u in range(m):
for v in range(n):
distance = np.sqrt((u-center_y)**2 + (v-center_x)**2)
PSF[u, v] = np.exp(-k * (distance** (5/3)))
PSF = PSF / PSF.sum()
return PSF
# 生成运动模糊核,原理是线段,模拟匀速运动模糊效果
def motion_PSF(kernel_size=30, angle=-45, length=20): # kernel_size是核大小,angle是运动方向,length是运动长度
PSF = np.zeros((kernel_size, kernel_size))
center = kernel_size // 2
angle_rad = np.deg2rad(angle)
x_start = center - 0.5 * length * np.cos(angle_rad)
y_start = center - 0.5 * length * np.sin(angle_rad)
x_end = center + 0.5 * length * np.cos(angle_rad)
y_end = center + 0.5 * length * np.sin(angle_rad)
cv2.line(PSF,
(int(x_start), int(y_start)),
(int(x_end), int(y_end)),
1, thickness=1)
PSF = PSF / PSF.sum()
return PSF
# 扩展PSF到图像尺寸
def extend_PSF(image, PSF_small): # image是图像,PSF_small是运动模糊核
h, w = image.shape
h_psf, w_psf = PSF_small.shape
PSF_large = np.zeros((h, w))
start_h = (h - h_psf) // 2
start_w = (w - w_psf) // 2
PSF_large[start_h:start_h+h_psf, start_w:start_w+w_psf] = PSF_small
return PSF_large
# 频域模糊处理
def apply_blur(image, PSF): # image是图像,PSF是运动模糊核
image_fft = np.fft.fft2(image)
PSF_fft = np.fft.fft2(np.fft.ifftshift(PSF))
blurred_fft = image_fft * PSF_fft
blurred = np.abs(np.fft.ifft2(blurred_fft))
return blurred
# 添加高斯噪声
def add_gaussian_noise(image, noise_level=0.01): # image是图像,noise_level是噪声强度
noise = np.random.normal(0, noise_level * image.std(), image.shape)
noisy_image = image + noise
return np.clip(noisy_image, 0, 1)
# 逆滤波复原
def inverse_filter(blurred, PSF, eps=1e-6): # blurred是模糊图像,PSF是运动模糊核,eps是防止除零的阈值
blurred_fft = np.fft.fft2(blurred)
PSF_fft = np.fft.fft2(np.fft.ifftshift(PSF))
PSF_fft = np.where(np.abs(PSF_fft) < eps, eps, PSF_fft)
restored_fft = blurred_fft / PSF_fft
restored = np.abs(np.fft.ifft2(restored_fft))
return restored
# 维纳滤波复原
def wiener_filter(blurred, PSF, K=0.01): # blurred是模糊图像,PSF是运动模糊核,K是噪声功率谱密度
blurred_fft = np.fft.fft2(blurred)
PSF_fft = np.fft.fft2(np.fft.ifftshift(PSF))
filter_fft = np.conj(PSF_fft) / (np.abs(PSF_fft)**2 + K)
restored_fft = blurred_fft * filter_fft
restored = np.abs(np.fft.ifft2(restored_fft))
return restored
# 约束最小二乘滤波复原
def constrained_least_squares(blurred, PSF, gamma=0.001):# blurred是模糊图像,PSF是运动模糊核,gamma是平滑参数
blurred_fft = np.fft.fft2(blurred)
PSF_fft = np.fft.fft2(np.fft.ifftshift(PSF))
h, w = blurred.shape
lap_kernel = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]])
lap_large = extend_PSF(blurred, lap_kernel)
lap_fft = np.fft.fft2(np.fft.ifftshift(lap_large))
filter_fft = np.conj(PSF_fft) / (np.abs(PSF_fft)**2 + gamma * np.abs(lap_fft)**2)
restored_fft = blurred_fft * filter_fft
restored = np.abs(np.fft.ifft2(restored_fft))
return restored
# 计算图像质量指标 ## MSE, PSNR, SSIM分别是均方误差,信噪比,结构相似度 ,其中SSIM是0-1之间,越接近1越好;PSNR是0-100之间,越接近100越好;MSE是0-1之间,越接近0越好
def calculate_metrics(original, restored):
mse = np.mean((original - restored) ** 2)
psnr = 20 * np.log10(1.0 / np.sqrt(mse)) if mse > 0 else float('inf')
from skimage.metrics import structural_similarity as ssim
ssim_val = ssim(original, restored, data_range=original.max() - original.min())
return mse, psnr, ssim_val
# 主程序
def main():
# 读取图像
image = cv2.imread('./img/adip.png', 0)
if image is None:
print("无法读取图像,请检查文件路径")
return
image = image.astype(np.float32) / 255.0
h, w = image.shape
print("图像尺寸:", image.shape)
print("生成退化图像...")
# 情况1: -45度平面匀速运动模糊
motion_psf1 = motion_PSF(30, angle=-45, length=25) #motion_PSF(核大小,运动角度,运动长度) 返回运动模糊核
psf1 = extend_PSF(image, motion_psf1)# extend_PSF(图像,运动模糊核) 返回扩展后的运动模糊核
blurred1 = apply_blur(image, psf1)# apply_blur(图像,运动模糊核) 返回模糊图像
# 情况2: 大气湍流模糊 + 高斯噪声
turbulence_psf = turbulence_PSF((h, w), k=0.001)
blurred2 = apply_blur(image, turbulence_psf)
noisy2 = add_gaussian_noise(blurred2, 0.02)
# 情况3: 120度平面匀速运动模糊 + 高斯噪声
motion_psf3 = motion_PSF(30, angle=120, length=20)
psf3 = extend_PSF(image, motion_psf3)
blurred3 = apply_blur(image, psf3)
noisy3 = add_gaussian_noise(blurred3, 0.015)
# 应用三种复原方法
print("进行图像复原...")
results = {}
# 情况1复原
results['case1'] = {
'degraded': blurred1,
'inverse': inverse_filter(blurred1, psf1, 1e-5),
'wiener': wiener_filter(blurred1, psf1, 0.005),
'cls': constrained_least_squares(blurred1, psf1, 0.001),
'psf': psf1,
'title': '-45°运动模糊'
}
# 情况2复原
results['case2'] = {
'degraded': noisy2,
'inverse': inverse_filter(noisy2, turbulence_psf, 1e-5),
'wiener': wiener_filter(noisy2, turbulence_psf, 0.01),
'cls': constrained_least_squares(noisy2, turbulence_psf, 0.005),
'psf': turbulence_psf,
'title': '大气湍流模糊+噪声'
}
# 情况3复原
results['case3'] = {
'degraded': noisy3,
'inverse': inverse_filter(noisy3, psf3, 1e-5),
'wiener': wiener_filter(noisy3, psf3, 0.008),
'cls': constrained_least_squares(noisy3, psf3, 0.003),
'psf': psf3,
'title': '120°运动模糊+噪声'
}
# 修改为4×4布局
print("生成4×4布局结果图像...")
fig, axes = plt.subplots(4, 4, figsize=(16, 16))
# 第一行:原始图像 + 三种PSF
axes[0, 0].imshow(image, cmap='gray')
axes[0, 0].set_title('原始图像', fontsize=12, fontweight='bold')
axes[0, 0].axis('off')
# 显示三种PSF(现在只有3列可用)
psf_titles = ['-45°运动模糊PSF', '大气湍流PSF', '120°运动模糊PSF']
psf_images = [motion_psf1, turbulence_psf, motion_psf3] # 使用小尺寸PSF显示更清晰
for i in range(3):
axes[0, i+1].imshow(psf_images[i], cmap='hot')
axes[0, i+1].set_title(psf_titles[i], fontsize=10)
axes[0, i+1].axis('off')
# 第二行开始:三种情况的复原结果
method_titles = ['退化图像', '逆滤波', '维纳滤波', '约束最小二乘']
case_keys = ['case1', 'case2', 'case3']
for row, case_key in enumerate(case_keys):
case = results[case_key]
# 显示退化图像
axes[row+1, 0].imshow(case['degraded'], cmap='gray')
axes[row+1, 0].set_title(f"{case['title']}\n退化图像", fontsize=10)
axes[row+1, 0].axis('off')
# 显示三种复原方法结果
methods = ['inverse', 'wiener', 'cls']
for col, method in enumerate(methods):
axes[row+1, col+1].imshow(case[method], cmap='gray')
axes[row+1, col+1].set_title(f"{method_titles[col+1]}", fontsize=10)
axes[row+1, col+1].axis('off')
# 第四行:添加定量分析结果或说明
axes[3, 0].text(0.5, 0.5, '实验总结\n\nPSNR/SSIM比较:\n• 逆滤波: 噪声敏感\n• 维纳滤波: 稳健平衡\n• 约束最小二乘: 平滑抑制',
ha='center', va='center', fontsize=11, transform=axes[3, 0].transAxes)
axes[3, 0].axis('off')
# 可以添加其他分析内容到剩余的三个位置
for i in range(1, 4):
axes[3, i].axis('off') # 暂时留空
plt.tight_layout()
plt.suptitle('图像退化与复原方法对比实验 (4×4布局)', fontsize=16, fontweight='bold', y=1.02)
plt.show()
# 定量分析(控制台输出)
print("\n" + "="*80)
print("定量分析结果")
print("="*80)
for case_key in case_keys:
case = results[case_key]
print(f"\n{case['title']} - 复原方法比较:")
print("-" * 50)
for method in ['inverse', 'wiener', 'cls']:
mse, psnr, ssim_val = calculate_metrics(image, case[method])
print(f"{method:>15}: MSE={mse:.6f}, PSNR={psnr:.2f}dB, SSIM={ssim_val:.4f}")
if __name__ == "__main__":
main()
定量分析结果👇
MSE, PSNR, SSIM分别是均方误差,信噪比,结构相似度 ,
- SSIM是0-1之间,越接近1越好;
- PSNR是0-100之间,越接近100越好;
- MSE是0-1之间,越接近0越好
-45°运动模糊 - 复原方法比较:
--------------------------------------------------
inverse: MSE=0.000000, PSNR=65.65dB, SSIM=0.9998✅最优
wiener: MSE=0.002322, PSNR=26.34dB, SSIM=0.7378
cls: MSE=0.000840, PSNR=30.76dB, SSIM=0.8436
结论:
- 逆滤波表现最佳:在无噪声的理想情况下,逆滤波几乎完美复原(PSNR 65.65dB,接近无损)
- 约束最小二乘效果次之,维纳滤波相对较差
- 这验证了逆滤波在无噪声条件下的理论最优性
大气湍流模糊+噪声 - 复原方法比较:
--------------------------------------------------
inverse: MSE=14648.655021, PSNR=-41.66dB, SSIM=-0.0000 ❌完全失效
wiener: MSE=0.029478, PSNR=15.30dB, SSIM=0.4117
cls: MSE=0.017128, PSNR=17.66dB, SSIM=0.3698
结论:
- 逆滤波完全失效:噪声被严重放大(MSE极大,PSNR为负值)
- 约束最小二乘在MSE和PSNR指标上优于维纳滤波
- 但维纳滤波在SSIM指标上略好,说明在结构保持方面有一定优势
- 约束最小二乘是这种情况下的最佳选择
120°运动模糊+噪声 - 复原方法比较:
--------------------------------------------------
inverse: MSE=2.826758, PSNR=-4.51dB, SSIM=0.0016 ❌较差
wiener: MSE=0.002654, PSNR=25.76dB, SSIM=0.6758
cls: MSE=0.001276, PSNR=28.94dB, SSIM=0.7787 ✅最优
结论:
- 约束最小二乘全面最优:在所有指标上都表现最好
- 维纳滤波效果次之,但仍远优于逆滤波
- 逆滤波再次显示出对噪声的敏感性
噪声敏感性排序: 逆滤波 >>> 维纳滤波 > 约束最小二乘最终结论:约束最小二乘法在现实场景(含噪声)中表现最为稳健,是大多数实际应用的首选方法。逆滤波虽然在理想条件下最优,但对噪声的敏感性限制了其实用性。维纳滤波在特定条件下可作为约束最小二乘的有效替代方案。

