第五章图像复原

yange大约 29 分钟数字图像处理数字图像处理

1. 图像复原的基本概念

前言

定义

图像复原是将降质了的图像恢复成原来的图像。根据引起图像退化的原因以及降质的先验知识，建立退化模型，再针对降质过程采取相反的方法来恢复图像。

图像的质量下降叫做退化。退化的形式有模糊、失真、有噪声等。如果我们对 退化的类型、机制和过程 都十分清楚，那么就可以利用其反过程来复原图像。

一、下面列子哪个是复原，哪个是增强

1️⃣ 修复一张旧照片，目标是去除上面的划痕、污渍和褪色，让它看起来像刚拍出来时一样。你有一个它本应如何应如何的目标。
2️⃣ 给一张正常的照片添加滤镜，比如提高饱和度让色彩更鲜艳，或者增加对比度让细节更突出。目的是让它“更好看 ”或“更有用 ”，而不是纠正错误。

答案：案例1是复原，案例2是增强

二、核心区别

特征	图像复原	图像增强
目标	客观保真度 - 逼近原始未退化的真实图像	主观质量 - 改善视觉效果或特定应用下的可用性
基础	依赖于退化模型（物理/数学）	依赖于人的视觉心理或后续任务的需求
评判标准	均方误差 (MSE)、峰值信噪比 (PSNR) 等定量等定量指标	主要依靠人眼的主观判断，难以用统一标准衡量
处理方式	通常是反向过程，如反卷积、滤波	通常是正向映射，如灰度变换、空间滤波

三、两者的紧密联系与协同工作

1️⃣ 尽管目标和思想不同，但在实际应用中，二者并非泾渭分明，而是常常协同工作，形成一个图像质量提升的提升的管道：

互补关系：一幅图像可能需要先进行复原，再进行增强。 👇
例如：在医学影像中：
第一步（复原）：使用算法去除CT图像中的设备噪声和伪影，这是复原。
第二步（增强）：然后对去噪后的噪后的图像进行对比度增强，使医生能更清晰地分辨病变组织，这是增强。

目标一致：最终目的都是为了让图像变得“更好”。 👈 👈

对于高级视觉任务（如图像识别、自动驾驶），一个清晰的、高质量的输入图像至关重要。无论是通过复原手段得到干净的数据，还是通过增强手段突出关键特征，都是在为下游任务服务。

2.噪声模型和噪声仿真

噪声模型

定义

在之前的图像处理学习中，我们已经了解了图像的构成和各种增强技术。大家可能会发现，无论算法多么优秀，在实际应用中，图像质量常常会受到一个关键因素的挑战——噪声。它就像是声音中的杂音，会干扰信息的纯净度。今天，我们就来系统地认识一下几种常见的图像噪声，并学习如何在Jupyter Notebook中模拟它们，这将为我们后续学习图像去噪技术打下坚实的基础。

一、常见图像噪声模型简介

噪声可以理解为在图像获取或传输过程中，由于传感器、信道或处理电路等因素引入的随机干扰。根据其概率密度函数（PDF）的不同，我们可以将其分为多种类型。

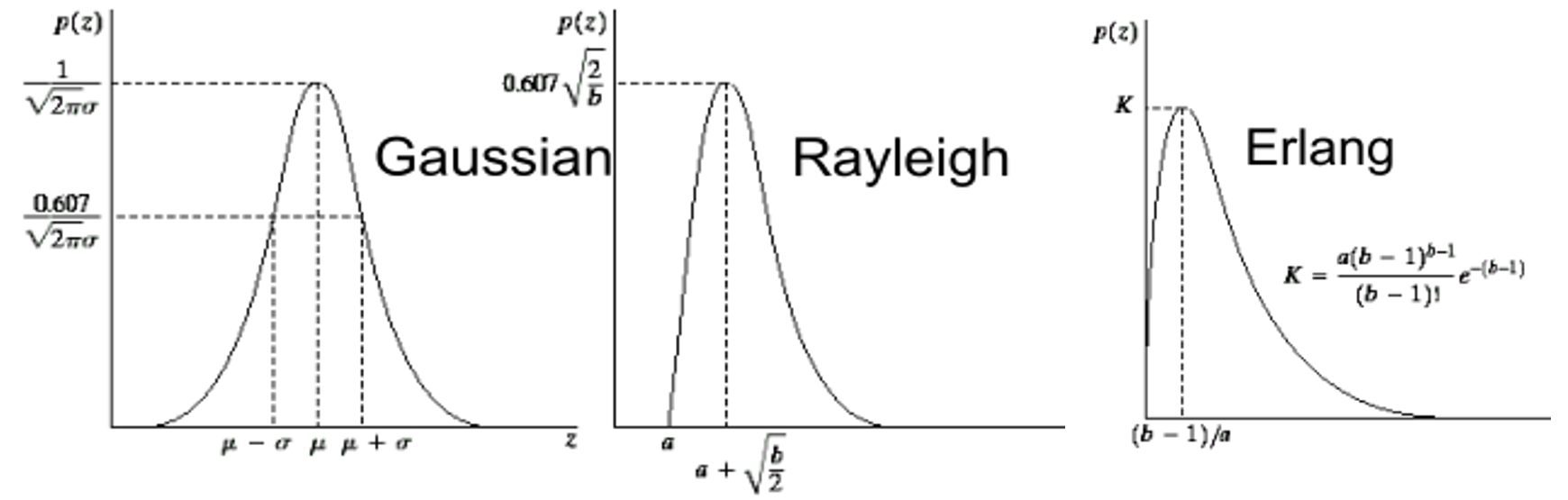
1. 高斯噪声 (Gaussian Noise)

这是最常见、最广为人知的一种噪声模型。正如自然界中许多随机变量都服从正态分布一样，高斯噪声也因其普遍性而成为我们研究噪声的噪声的起点。

特点： 其PDF服从高斯分布（即正态分布）。它在图像中表现为每个像素值上都叠加了一个微小的、随机的灰度变化。
成因： 主要来源于电子电路噪声，如传感器在高温工作时的热噪声。
直观感受：看起来像是一层细腻层细腻的“沙粒”或“薄膜”覆盖在图像上。

2. 瑞利噪声利噪声 (Rayleigh Noise)

当我们离开完美的对称世界（高斯），就会遇到一些有偏态的分布。瑞利噪声就是其中之一，它的分布形状不像高斯那样对称。

特点：PDF服从瑞利分布。该分布在原点处从0开始，形状向右偏移。
成因：常见于某些雷达成像以及医学超声图像中。
直观感受：对图像整体亮度的改变比高斯噪声更不均匀。

3. 伽马噪声 (Gamma Noise) / 厄兰噪声 (Erlang Noise)

伽马噪声是另一个非对称分布的典型代表，它与瑞利噪声类似，但形态可以由参数控制，更为灵活。

特点：PDF服从伽马分布（当形状参数为参数为整数时，也称为厄兰分布）。其曲线也是从0开始，向右偏斜。
成因：在激光成像等应用中较为常见。
直观感受 ：与瑞利噪声效果相似，都会导致图像出现偏向某一侧的亮度失真。

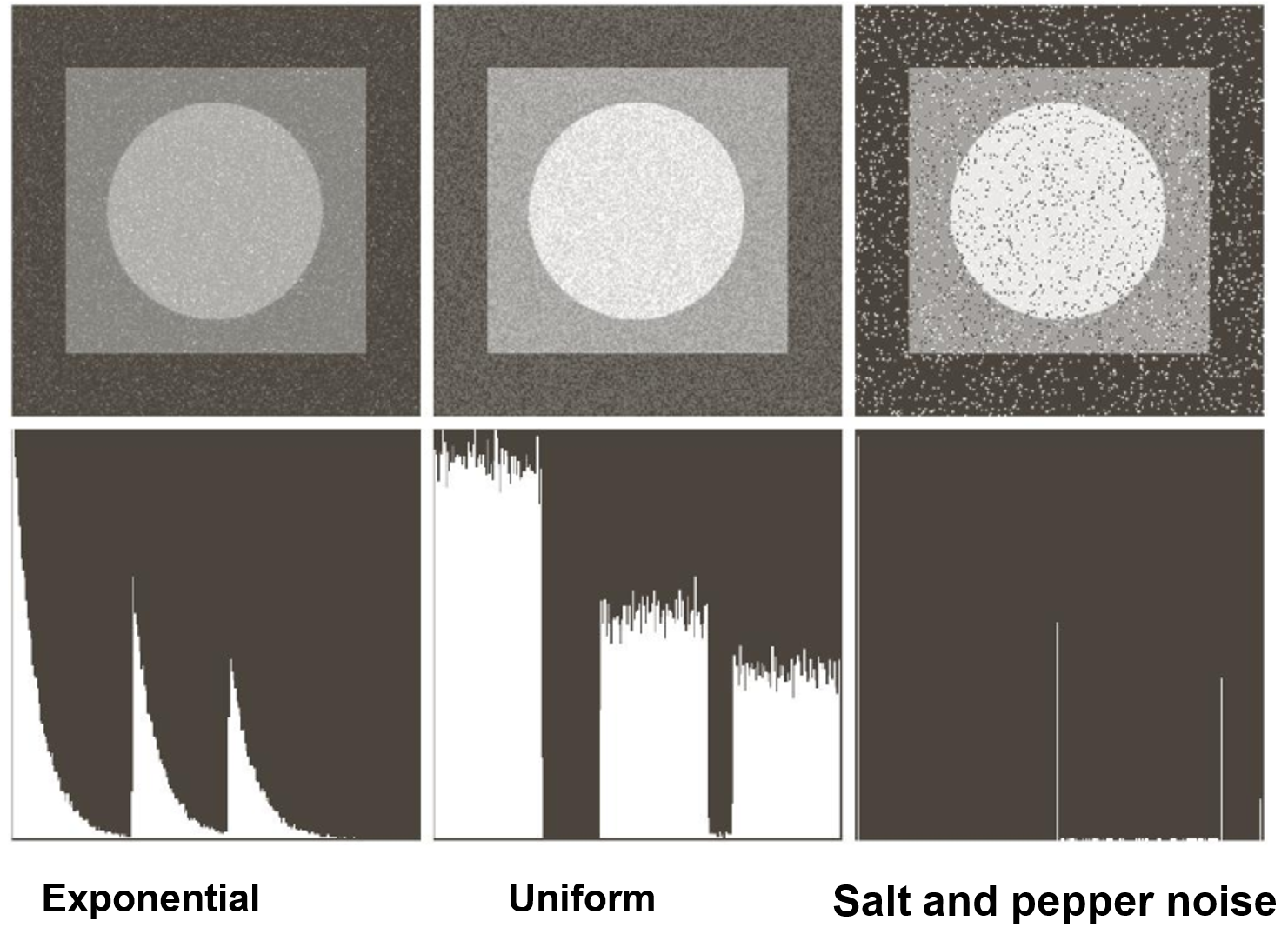
4. 指数噪声 (Exponential Noise)

如果我们把伽马噪声的特例推到极致，就得到了指数噪声。它是伽马分布在形状参数为1时的特殊形式。

特点：PDF服从指数分布。它是所有噪声模型中模型中衰减最“慢”的一种，有一个很长的“尾巴”。
成因：在激光成像中偶有出现。
直观感受：会产生比较强烈的、孤立的亮点或暗点区域

5. 均匀噪声 (Uniform Noise)

前面几种噪声的概率都不是均等的，现在我们来看一种最简单的等概率噪声——均匀噪声。

特点特点：PDF服从均匀分布。在一个给定的范围内，每个噪声值的出现概率是完全相同的。
成因：通常在仿真实验中作为其他噪声的基础，或者在量化误差中起到中起到一定作用。
直观感受：给图像增加了一种相对平缓、颗粒感一致的随机纹理。

6. 椒盐噪声 (Salt-and-Pepper Noise) / 脉冲噪声 (Impulse Noise)

最后，我们来认识一种风格迥异的噪声。它与前五种连续的加性噪声不同，是一种极端的、离散的替换性噪声。

特点：像素值会以一定的概率被突然置为极小值（胡椒，黑色）或极大值（盐粒，白色，白色）。
成因：通常由快速的瞬态干扰引起，例如，例如相机传感器上的坏点、传输信道的误码等。
直观感受：图像上随机散布着纯白和纯黑的像素点，就像撒了椒盐一样。

二、噪声仿真代码

下面我们将在一张干净的图像上，逐一添加上述噪声，并观察效果。

import numpy as np
import matplotlib.pyplot as plt
import cv2

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

def add_gaussian_noise(image, mean=0, sigma=25):
    """
    添加高斯噪声 - 服从正态分布，适合模拟传感器噪声
    Args:
        image: 输入图像
        mean: 噪声均值
        sigma: 噪声标准差
    """
    noise = np.random.normal(mean, sigma, image.shape)
    noisy_image = np.clip(image.astype(np.float32) + noise, 0, 255)
    return noisy_image.astype(np.uint8)

def add_rayleigh_noise(image, scale=30):
    """
    添加瑞利噪声 - 在雷达图像处理中常见
    Args:
        image: 输入图像
        scale: 瑞利分布的尺度参数
    """
    noise = np.random.rayleigh(scale, image.shape)
    noisy_image = np.clip(image.astype(np.float32) + noise, 0, 255)
    return noisy_image.astype(np.uint8)

def add_gamma_noise(image, shape=2.0, scale=10.0):
    """
    添加伽马噪声 - 适合模拟某些光学成像系统的噪声
    Args:
        image: 输入图像
        shape: 伽马分布的形状参数
        scale: 伽马分布的尺度参数
    """
    noise = np.random.gamma(shape, scale, image.shape)
    noisy_image = np.clip(image.astype(np.float32) + noise, 0, 255)
    return noisy_image.astype(np.uint8)

def add_exponential_noise(image, scale=25.0):
    """
    添加指数噪声 - 在激光成像中常见
    Args:
        image: 输入图像
        scale: 指数分布的尺度参数
    """
    noise = np.random.exponential(scale, image.shape)
    noisy_image = np.clip(image.astype(np.float32) + noise, 0, 255)
    return noisy_image.astype(np.uint8)

def add_uniform_noise(image, low=-20, high=20):
    """
    添加均匀噪声 - 最简单的随机噪声
    Args:
        image: 输入图像
        low: 均匀分布的下界
        high: 均匀分布的上界
    """
    noise = np.random.uniform(low, high, image.shape)
    noisy_image = np.clip(image.astype(np.float32) + noise, 0, 255)
    return noisy_image.astype(np.uint8)

def add_salt_pepper_noise(image, salt_prob=0.01, pepper_prob=0.01):
    """
    添加椒盐噪声 - 模拟图像传输中的脉冲噪声
    Args:
        image: 输入图像
        salt_prob: 盐噪声概率（白点）
        pepper_prob: 椒噪声概率（黑点）
    """
    noisy_image = image.copy()
    salt_mask = np.random.random(image.shape) < salt_prob
    pepper_mask = np.random.random(image.shape) < pepper_prob
    noisy_image[salt_mask] = 255
    noisy_image[pepper_mask] = 0
    return noisy_image

# 主程序
try:
    # 加载图像（如果指定路径不存在，使用内置示例）
    image_path = './img/train_.jpg'
    
    # 尝试加载指定图像，如果失败则创建示例图像
    try:
        img = cv2.imread(image_path)
        if img is None:
            raise FileNotFoundError
        gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        print(f"成功加载图像: {image_path}")
    except:
        # 创建示例图像：256x256的渐变灰度图
        print("未找到指定图像，创建示例图像...")
        gray_img = np.zeros((256, 256), dtype=np.uint8)
        for i in range(256):
            gray_img[i, :] = i  # 创建垂直渐变
        print("已创建示例渐变图像")

    # 添加各种噪声
    print("正在为图像添加各种噪声...")
    
    noisy_images = [
        gray_img,
        add_gaussian_noise(gray_img),
        add_rayleigh_noise(gray_img),
        add_gamma_noise(gray_img),
        add_exponential_noise(gray_img),
        add_uniform_noise(gray_img),
        add_salt_pepper_noise(gray_img)
    ]
    
    titles = [
        '原始灰度图像',
        '高斯噪声 (μ=0, σ=25)',
        '瑞利噪声 (scale=30)',
        '伽马噪声 (shape=2, scale=10)',
        '指数噪声 (scale=25)',
        '均匀噪声 (low=-20, high=20)',
        '椒盐噪声 (salt=1%, pepper=1%)'
    ]

    # 创建图像显示
    plt.figure(figsize=(18, 12))
    
    for i in range(7):
        plt.subplot(3, 3, i+1)
        plt.imshow(noisy_images[i], cmap='gray')
        plt.title(titles[i], fontsize=12)
        plt.axis('off')
    
    plt.tight_layout()
    plt.show()

    # 显示噪声统计信息
    print("\n" + "="*60)
    print("噪声类型说明:")
    print("="*60)
    print("1. 高斯噪声: 服从正态分布，适合模拟传感器噪声")
    print("2. 瑞利噪声: 在雷达图像处理中常见")
    print("3. 伽马噪声: 适合模拟某些光学成像系统的噪声") 
    print("4. 指数噪声: 在激光成像中常见")
    print("5. 均匀噪声: 最简单的随机噪声")
    print("6. 椒盐噪声: 模拟图像传输中的脉冲噪声")
    print("="*60)

except Exception as e:
    print(f"程序执行出错: {e}")

3.滤波去噪方法之空域滤波

滤波去噪方法

定义

在前面的学习案例中，我们看到不同类型噪声对图像造成了各异的破坏。现在，我们要拿起"工具箱 "里的各种滤波器，针对性地修复这些损伤。

空域滤波直接在图像像素上进行操作，通过在局部邻域内执行特定运算来估计真实像素值。

主要分为三类： 👇

均值滤波系列：通过邻域平均来平滑噪声
顺序统计滤波：基于排序的鲁棒方法
自适应滤波：智能调整参数的先进技术

下面我们逐一详细介绍每种滤波器的工作原理和应用场景。

一、均值滤波家族

均值滤波器的基本思想是用邻域内像素的平均值来代替中心像素，从而抑制噪声。

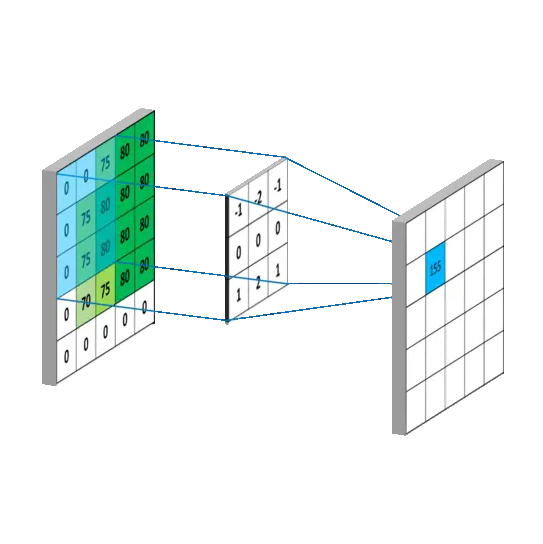
1. 算术均值滤波 (Arithmetic Mean Filter)

这是最简单直接的均值滤波器。

工作原理：

定义一个大小为m×n的滑动窗口
计算窗口内所有像素的算术平均值
用该用该平均值替换中心像素值

数学表达式：

f(x,y) = (1/mn) × Σg(s,t)
         (s,t)∈S_xy

g(s,t)为退化图像，f(x,y)为去噪的估计图像

优缺点：

✅ 优点：计算简单，对高斯噪声有一定效果
❌ 缺点：会导致图像模糊，丢失边缘细节

2. 几何均值滤波 (Geometric Mean Filter)

相比算术均值，几何均值能保留更多图像细节。

工作原理：

计算邻域内所有像素值的乘积,并累加
对该乘积开1/nm次方

数学表达式：

f(x,y) = [Π g(s,t)]^(1/mn)
         (s,t)∈S_xy

g(s,t)为退化图像，f(x,y)为去噪的估计图像

优缺点：
✅ 优点：比算术均值更好的细节保存能力
❌ 缺点：对零值敏感（乘积为零则结果为0）

3. 谐波均值滤波 (Harmonic Mean Filter)

对盐噪声（白点）特别有效。

工作原理：

计算邻域内像素值的倒数之和
用邻域像素总数除以这个和

数学表达式：

f(x,y) = mn / Σ [1/g(s,t)]
           (s,t)∈S_xy

g(s,t)为退化图像，f(x,y)为去噪的估计图像

4. 逆谐波均值滤波 (Contra-harmonic Mean Filter)

这是最灵活的均值滤波器，可通过参数Q来控制滤波行为。

工作原理：

计算邻域内像素值的(Q+1)次方次方之和
除以像素值的Q次方之和

数学表达式：

 f(x,y) = Σ [g(s,t)]^(Q+1) / Σ [g(s,t)]^Q
         (s,t)∈S_xy       (s,t)∈S_xy

g(s,t)为退化图像，f(x,y)为去噪的估计图像

滤波行为控制：

Q > 0：消除胡椒噪声
Q < 0：消除盐噪声
Q = 0：退化为算术均值滤波
Q = -1：退化为谐波均值滤波

二、中值滤波及其改进

5. 标准中值滤波 (Median Filter)

非线性滤波的代表，对脉冲噪声极其有效。

工作原理：

将邻域内像素值按从小到大排序
取中间位置的数值作为中心像素的新值

数学表达式：

 g(x,y) = median {f(s,t)}
         (s,t)∈S_xy

优缺点：
✅ 优点：有效去除椒盐噪声，保持边缘清晰
❌ 缺点：对大窗口会过度平滑，损失细节

6. 自适应中值滤波 (Adaptive Median Filter)

智能化的中值滤波，能自动调整策略。

承上启下：标准中值滤波虽然强大，但在高噪声密度下性能下降，且固定窗口尺寸不够灵活。自适应中值滤波应运而生，它像一个经验丰富的医生，会根据"病情"调整"治疗方案"。

核心优势：

🎯 动态调整窗口大小
🔍 区分噪声点和信号点
💡 在高噪声密度下仍保持良好性能

算法流程：

阶段A：判断中值是否受污染

A1 = Z_med - Z_min
A2 = Z_med - Z_max

Z_med： S_xy集合中灰度值的中值
Z_min： S_xy集合中灰度值最小值
Z_max： S_xy集合中灰度值最大值

如果A1>0且A2<0，转到阶段B；否则增大窗口尺寸，重复阶段A直到达到最大窗口尺寸。

阶段B：判断中心像素是否受污染

B1 = Z_xy - Z_min
B2 = Z_xy - Z_max

如果B1>0且B2<0，输出Z_xy（认为是信号）；否则输出Z_med（认为是噪声）

三、知识总结：🍐❤️ 👈

📊 均值滤波族：适合高斯类噪声，但会模糊图像
⚡ 中值滤波：椒盐噪声的克星，保边效果好
🤖 自适应滤波：智能化选择，适应复杂场景

4. 滤波去噪方法之频域滤波

前言

定义

在掌握了空域滤波的各种技巧之后，我们现在要进入一个更加宏观和强大的领域——频域滤波

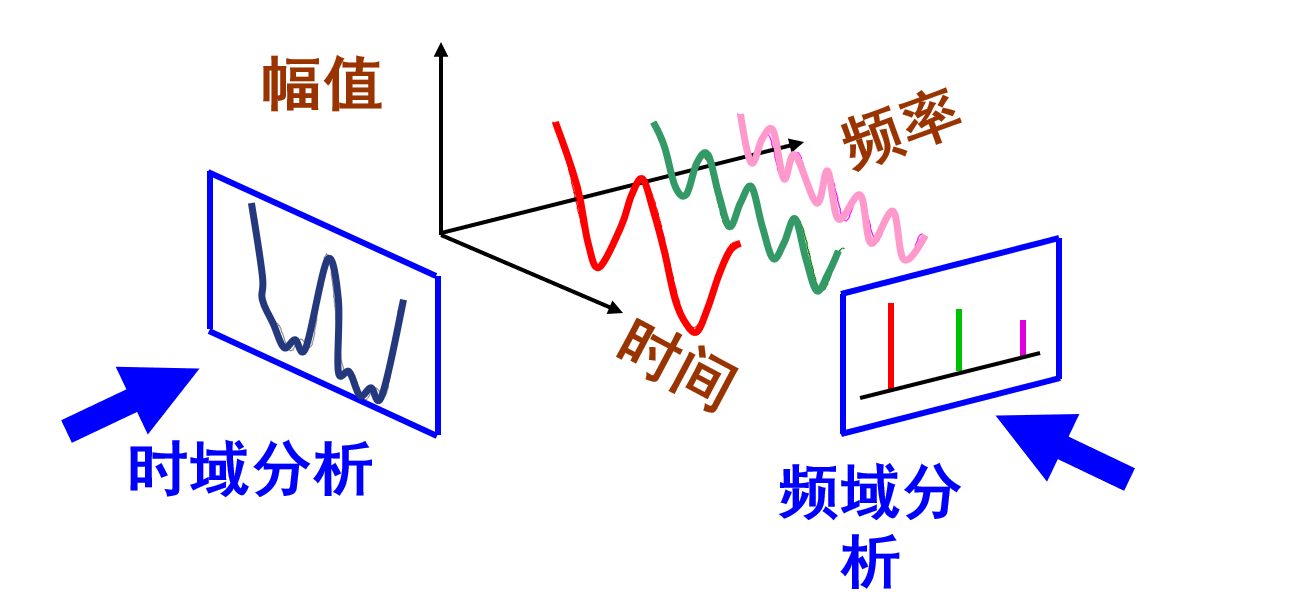
如果说 空域滤波 像是我们用放大镜一寸寸地修复照片，那么频域滤波就如同一位音乐指挥家，他能看到整个乐谱的频率组成，精准地减弱不和谐的杂音，同时保留主旋律的完整性。这种方法不是直接在像素上操作，而是先将图像变换到频率域，在那里噪声往往具有独特的"声纹特征"，使我们能够更精确地靶向清除。

频域滤波的基本原理

核心思想：任何图像都可以分解为不同频率的正弦波组合。

低频成分：对应图像的平坦区域、总体轮廓
高频成分：对应图像的边缘、细节、噪声

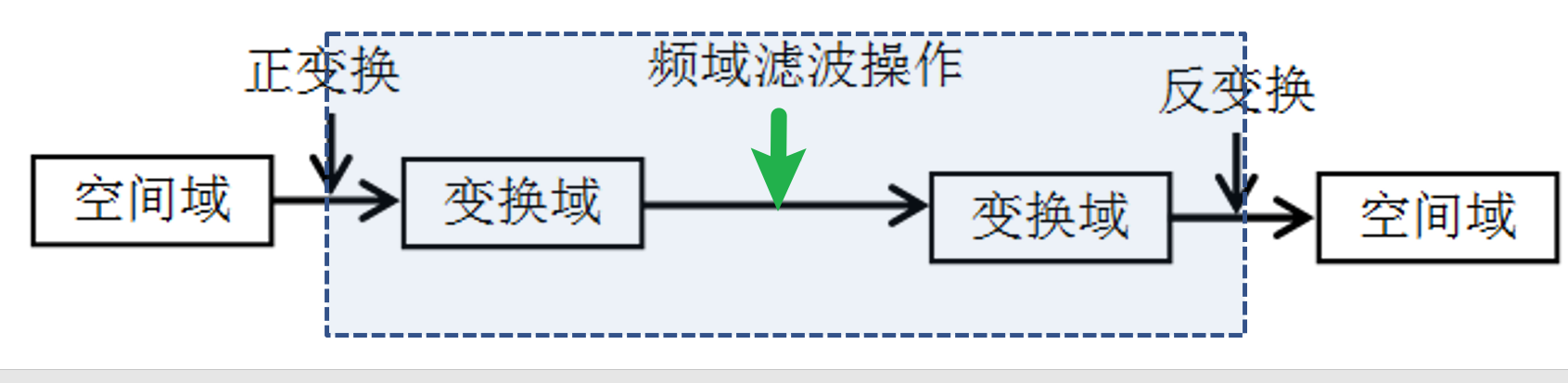
处理流程：

正向傅里叶变换 ：将图像从空域转换到频域
频域滤波：在频域中修改频率成分
逆向傅里叶变换 ：将处理后的结果还原回空域

一、带阻滤波器 (Band-Reject Filters)

在现实中，很多噪声并不是遍布所有频率，而是集中在某个特定的频率带上。比如周期性噪声（来自扫描仪振动、电气干扰等）就在频域中表现为孤立的亮点。带阻滤波器就像是一个频率范围的"剪刀 "，专门剪掉这些特定的噪声带。

1.1 理想带阻滤波器 (Ideal Band-Reject Filter)

最直接的阻断方式，但有明显的振铃效应。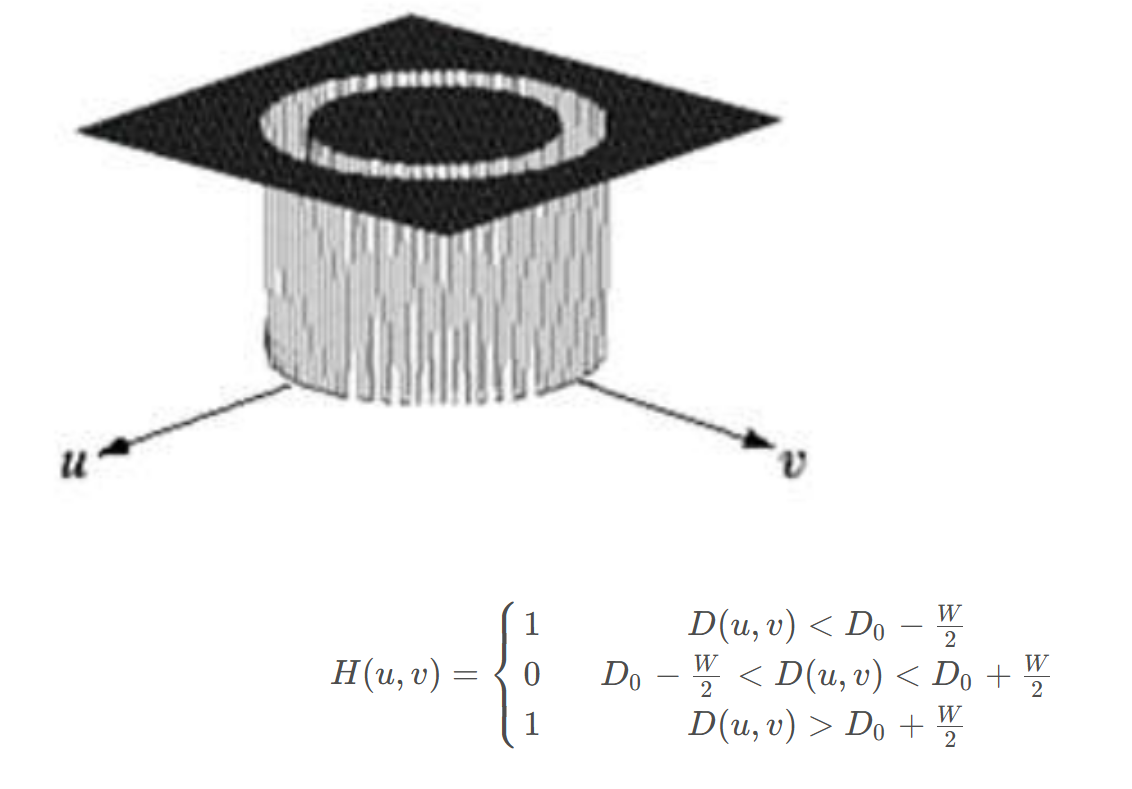

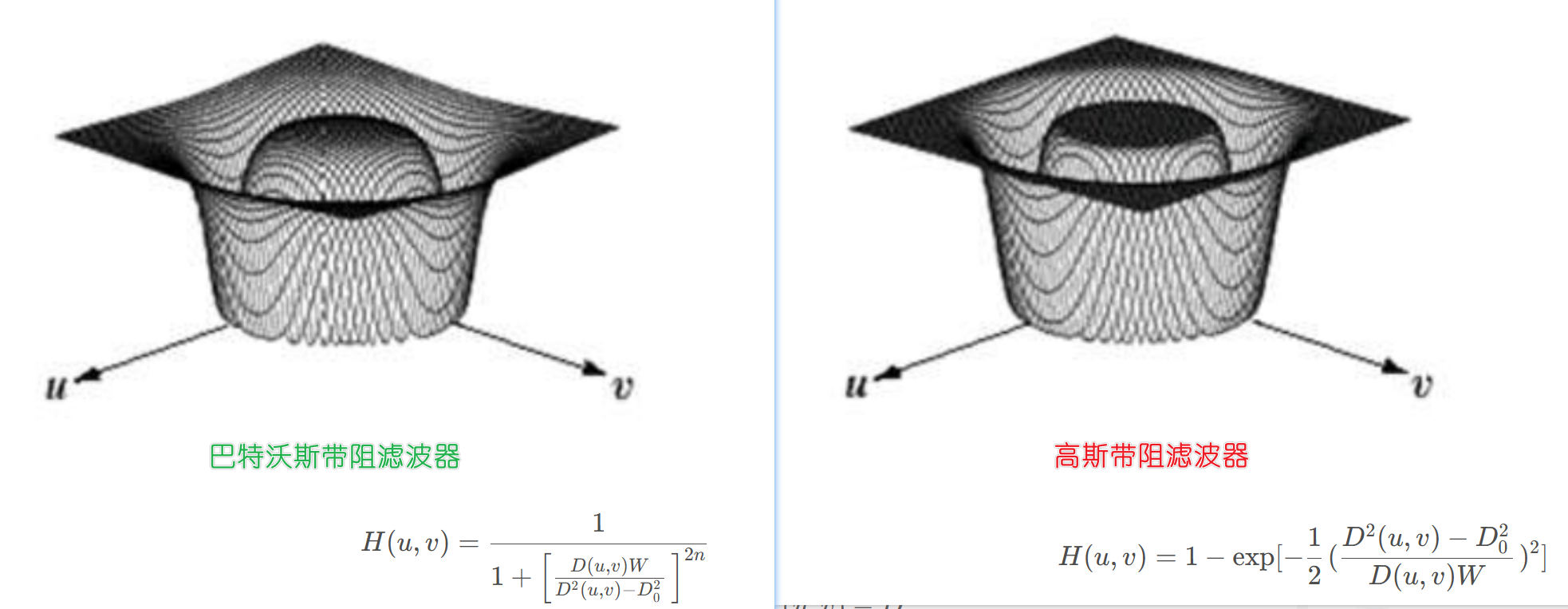
1.2 高斯带阻滤波器 (Gaussian Band-Reject Filter)

过渡平滑，避免了振铃效应

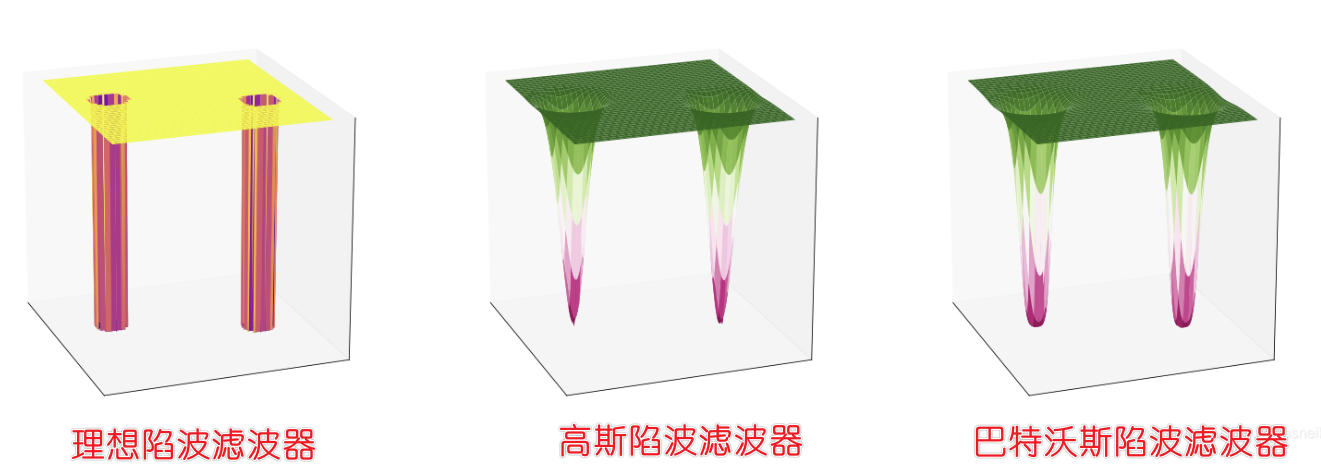
二、陷波滤波器 (Notch Filters)

带阻滤波器虽然有用，但它有时过于粗暴，会把有用的频率信息也一起阻断。陷波滤波器则像是一位精确的外科医生，只切除病灶，尽可能保留健康组织.

2.1 基本原理

目标：选择性去除特定频率点处的干扰
特点：在频域中针对多个离散的噪声点进行处理
优势：比带阻滤波器更具选择性

三、二值遮罩滤波器 (Binary Mask Filters)

有时候，最高效的方法就是最简单的方法。二值遮罩滤波器采用"非黑即白"的策略，在频域中直接用0或1来允许或阻止频率成分通过。

基本原理
思想：手工或半自动地在频域中绘制遮罩
适用场景：噪声模式不规则，无法用简单的数学公式描述
灵活性：可以根据具体问题的需求定制
注意事项：傅里叶变换具有对称性，因此遮罩的绘制需要考虑到这一点

四、案例演示

案例图片制作

import cv2
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

# 读取图像并转换为灰度图
img = cv2.imread(r'./img/peppers.bmp',0)

# 对图像进行二维傅里叶变换
F = np.fft.fft2(img)

# 将频谱的零频率分量移到频谱中心
fshift0 = np.fft.fftshift(F)

# 创建频谱的副本用于修改
G = fshift0.copy()

# 获取频谱的最大幅值
fmax = np.max(np.abs(fshift0))

# 获取图像尺寸
m, n = F.shape

# 计算图像中心坐标
u0, v0 = m//2, n//2  # 图像中心

# 第一组频率点：在垂直方向上偏移
r1 = 50
u1 = u0
v1 = v0 - r1  # 中心上方50像素
G[u1, v1] = fmax/5  # 设置该频率点的幅值为最大值的1/5

# 设置对称点（根据傅里叶变换的对称性）
u2 = m - 1 - u1
v2 = n - 1 - v1
G[u2, v2] = fmax/5



# 创建显示窗口
plt.figure(figsize=(20, 10))

# 显示修改后的频谱（使用对数变换增强可视化效果）
plt.subplot(121)
plt.imshow(20*np.log(1+abs(G)), cmap='gray')
plt.title('修改后的频谱')

# 逆变换：将频谱移回原始位置
f1 = np.fft.ifftshift(G)

# 逆傅里叶变换重构图像
img1 = abs(np.fft.ifft2(f1))

# 显示重构后的图像
plt.subplot(122)
plt.imshow(img1, cmap='gray')
plt.title('重构图像')
# 保存图像img1
cv2.imwrite('./img/peppers_new.jpg', img1)

plt.show()

各种滤波器展示

import cv2
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format="retina"
plt.rcParams['font.sans-serif'] = ['SimHei']  # 正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False    # 正常显示负号

# 读取含噪声的图像并转换为灰度图
try:
    img = cv2.imread('./img/peppers_new.jpg', 0)  # 0表示以灰度图模式读取
    if img is None:
        raise FileNotFoundError
    print(f"成功加载图像，尺寸: {img.shape}")
except FileNotFoundError:
    print("未找到图像文件，创建示例噪声图像用于演示...")
    # 创建含水平周期噪声的示例图像
    img = np.zeros((512, 512), dtype=np.uint8)
    for i in range(512):
        for j in range(512):
            img[i, j] = 128 + 64 * np.sin(0.15*j)  # 水平周期噪声
    img = np.clip(img, 0, 255).astype(np.uint8)

# 显示原始含噪声图像
plt.figure(figsize=(8, 6))
plt.imshow(img, cmap='gray')
plt.title('含水平周期噪声的原始图像')
plt.axis('off')
plt.show()

# ============================================================================
# 傅里叶变换与频谱分析
# ============================================================================

def image_fft(image):
    """对图像进行傅里叶变换并返回中心化频谱"""
    f = np.fft.fft2(image)  # 傅里叶变换
    fshift = np.fft.fftshift(f)  # 频谱中心化
    magnitude_spectrum = 20 * np.log(np.abs(fshift) + 1)  # 幅度谱（用于显示）
    return fshift, magnitude_spectrum

def image_ifft(fshift):
    """对中心化频谱进行逆傅里叶变换并返回重构图像"""
    f_ishift = np.fft.ifftshift(fshift)  # 逆中心化
    img_back = np.fft.ifft2(f_ishift)  # 逆傅里叶变换
    img_back = np.abs(img_back)  # 取模值（实部）
    return np.clip(img_back, 0, 255).astype(np.uint8)

# 对噪声图像进行傅里叶变换
noisy_freq, noisy_spectrum = image_fft(img)

# 显示噪声图像的频谱（水平噪声对应频谱中的垂直线）
plt.figure(figsize=(8, 6))
plt.imshow(noisy_spectrum, cmap='gray')
plt.title('噪声图像的频谱图（垂直线对应水平噪声）')
plt.axis('off')
plt.colorbar(label='对数幅度')
plt.show()

# ============================================================================
# 三种滤波器实现（陷波和二值遮罩针对水平方向噪声）
# ============================================================================

def create_gaussian_bandreject_filter(shape, d0=30, w=10):
    """创建高斯带阻滤波器（针对垂直频谱线，即水平噪声）"""
    rows, cols = shape
    u, v = np.meshgrid(np.arange(cols), np.arange(rows))
    
    # 计算到中心的距离
    d = np.sqrt((u - cols/2)**2 + (v - rows/2)**2)
    
    # 高斯带阻滤波器公式
    gbr = 1 - np.exp(-0.5 * ((d**2 - d0**2) / (d * w + 1e-6))**2)
    return gbr

def create_gaussian_notch_filter(shape, notch_centers, radius=5):
    """创建高斯陷波滤波器（针对水平方向噪声，精确消除垂直线频谱）"""
    rows, cols = shape
    u, v = np.meshgrid(np.arange(cols), np.arange(rows))
    
    h = np.ones((rows, cols))  # 初始化为全1矩阵（全通）
    
    for (u0, v0) in notch_centers:
        # 计算到陷波中心的距离
        d = np.sqrt((u - u0)**2 + (v - v0)**2)
        
        # 高斯陷波（在陷波中心区域衰减）
        notch = 1 - np.exp(-(d**2) / (2 * radius**2))
        h *= notch
        
        # 处理共轭对称点（傅里叶变换对称性要求）
        u_conj = cols - u0
        v_conj = rows - v0
        d_conj = np.sqrt((u - u_conj)**2 + (v - v_conj)**2)
        notch_conj = 1 - np.exp(-(d_conj**2) / (2 * radius**2))
        h *= notch_conj
    
    return h

def create_binary_mask_filter(shape, notch_centers, radius=5):
    """创建二值遮罩滤波器（针对水平方向噪声，完全遮挡垂直线频谱）"""
    rows, cols = shape
    u, v = np.meshgrid(np.arange(cols), np.arange(rows))
    
    h = np.ones((rows, cols))  # 初始化为全1矩阵（全通）
    
    for (u0, v0) in notch_centers:
        # 计算到陷波中心的距离
        d = np.sqrt((u - u0)**2 + (v - v0)**2)
        
        # 创建圆形遮罩，在半径内的点设为0（完全阻隔）
        mask = d <= radius
        h[mask] = 0
        
        # 处理共轭对称点
        u_conj = cols - u0
        v_conj = rows - v0
        d_conj = np.sqrt((u - u_conj)**2 + (v - v_conj)**2)
        mask_conj = d_conj <= radius
        h[mask_conj] = 0
    
    return h

# ============================================================================
# 噪声频率分析与滤波处理（针对水平方向噪声）
# ============================================================================

rows, cols = img.shape
center_u, center_v = cols // 2, rows // 2  # 频谱中心

# 水平噪声在频谱中表现为垂直线，设置这些噪声线位置（针对水平方向噪声）
noise_centers = [
    (center_u - 50, center_v),  # 左侧垂直线噪声      大家注意了，修改这里可以改参数，将黑色区域覆盖白点，观察效果图
    (center_u + 50, center_v)   # 右侧垂直线噪声（对称点）
]

# 创建三种滤波器
print("创建三种滤波器...")




# 1. 高斯带阻滤波器（针对垂直频谱线，即水平噪声）
gbr_filter = create_gaussian_bandreject_filter(
    shape=img.shape, 
    d0=50,    # 噪声频率中心（与垂直线位置对应）
    w=15      # 带宽
)

# 2. 高斯陷波滤波器（精确消除垂直线频谱，针对水平噪声）
gn_filter = create_gaussian_notch_filter(
    shape=img.shape,
    notch_centers=noise_centers,  # 垂直线噪声位置
    radius=6  # 陷波半径，黑色圈圈的大小
)

# 3. 二值遮罩滤波器（完全遮挡垂直线频谱，针对水平噪声）
bm_filter = create_binary_mask_filter(
    shape=img.shape,
    notch_centers=noise_centers,  # 垂直线噪声位置
    radius=6  # 遮罩半径  ，黑色圈圈的大小
)

# 应用滤波器并重构图像
print("应用滤波器并重构图像...")

# 高斯带阻滤波
gbr_freq = noisy_freq * gbr_filter
gbr_img = image_ifft(gbr_freq)
gbr_spectrum = 20 * np.log(np.abs(gbr_freq) + 1)

# 高斯陷波滤波（针对水平噪声）
gn_freq = noisy_freq * gn_filter
gn_img = image_ifft(gn_freq)
gn_spectrum = 20 * np.log(np.abs(gn_freq) + 1)

# 二值遮罩滤波（针对水平噪声）
bm_freq = noisy_freq * bm_filter
bm_img = image_ifft(bm_freq)
bm_spectrum = 20 * np.log(np.abs(bm_freq) + 1)

# ============================================================================
# 滤波结果对比显示
# ============================================================================

# 创建对比显示窗口
plt.figure(figsize=(18, 16))

# 原始图像与频谱
plt.subplot(4, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('原始含水平噪声图像')
plt.axis('off')

plt.subplot(4, 3, 2)
plt.imshow(noisy_spectrum, cmap='gray')
plt.title('原始频谱（垂直线为噪声）')
plt.axis('off')

# 高斯带阻滤波结果
plt.subplot(4, 3, 4)
plt.imshow(gbr_filter, cmap='gray')
plt.title('高斯带阻滤波器')
plt.axis('off')

plt.subplot(4, 3, 5)
plt.imshow(gbr_spectrum, cmap='gray')
plt.title('带阻滤波后频谱')
plt.axis('off')

plt.subplot(4, 3, 6)
plt.imshow(gbr_img, cmap='gray')
plt.title('带阻滤波后图像')
plt.axis('off')

# 高斯陷波滤波结果（针对水平噪声）
plt.subplot(4, 3, 7)
plt.imshow(gn_filter, cmap='gray')
plt.title('高斯陷波滤波器（水平噪声）')
plt.axis('off')

plt.subplot(4, 3, 8)
plt.imshow(gn_spectrum, cmap='gray')
plt.title('陷波滤波后频谱')
plt.axis('off')

plt.subplot(4, 3, 9)
plt.imshow(gn_img, cmap='gray')
plt.title('陷波滤波后图像（水平噪声消除）')
plt.axis('off')

# 二值遮罩滤波结果（针对水平噪声）
plt.subplot(4, 3, 10)
plt.imshow(bm_filter, cmap='gray')
plt.title('二值遮罩滤波器（水平噪声）')
plt.axis('off')

plt.subplot(4, 3, 11)
plt.imshow(bm_spectrum, cmap='gray')
plt.title('遮罩滤波后频谱')
plt.axis('off')

plt.subplot(4, 3, 12)
plt.imshow(bm_img, cmap='gray')
plt.title('遮罩滤波后图像（水平噪声消除）')
plt.axis('off')

plt.tight_layout()
plt.show()

# ============================================================================
# 滤波效果定量分析
# ============================================================================

def calculate_psnr(original, filtered):
    """计算峰值信噪比（评估去噪效果）"""
    mse = np.mean((original - filtered) ** 2)
    return 20 * np.log10(255.0 / np.sqrt(mse)) if mse > 0 else float('inf')

# 计算三种方法的PSNR（以最佳滤波结果为参考）
ref_img = np.mean([gbr_img, gn_img, bm_img], axis=0).astype(np.uint8)
psnr_gbr = calculate_psnr(ref_img, gbr_img)
psnr_gn = calculate_psnr(ref_img, gn_img)
psnr_bm = calculate_psnr(ref_img, bm_img)

# 并排显示三种滤波结果
plt.figure(figsize=(18, 6))
plt.subplot(1, 3, 1)
plt.imshow(gbr_img, cmap='gray')
plt.title(f'高斯带阻滤波 (PSNR: {psnr_gbr:.2f} dB)')
plt.axis('off')

plt.subplot(1, 3, 2)
plt.imshow(gn_img, cmap='gray')
plt.title(f'高斯陷波滤波 (PSNR: {psnr_gn:.2f} dB)')
plt.axis('off')

plt.subplot(1, 3, 3)
plt.imshow(bm_img, cmap='gray')
plt.title(f'二值遮罩滤波 (PSNR: {psnr_bm:.2f} dB)')
plt.axis('off')

plt.tight_layout()
plt.show()

关键结论:

PSNR全称：峰值信噪比（Peak Signal-to-Noise Ratio），表示信号与噪声的比值，越大越好。单位是dB。
水平周期噪声在频谱中表现为垂直线条，通过消除这些线条可有效去噪
高斯陷波滤波效果最佳：精准去除噪声频率，同时保留图像细节
二值遮罩滤波虽然能去除噪声，但容易引入振铃效应
高斯带阻滤波适合噪声频率分布较宽的场景，但可能损失部分细节

5. 图像退化模型

图像退化模型

定义

一、引言：什么是图像退化？

图像复原实际上是图像退化的逆过程，如果弄清楚了图像退化的过程，那么久可以利用其逆过程来复原图片。

图像退化是指图像在形成、传输或记录过程中，由于各种因素导致质量下降的现象。

就像用老式相机拍摄快速移动的物体，或者透过毛玻璃看东西，图像会变得模糊不清。

图像退化就像"看花眼"，想象你戴着脏眼镜看世界：

镜片上的污渍让所有东西都变模糊 → 这就是"退化"
不同污渍造成不同模糊效果 → 不同的"退化模型"

二、图像退化模型的基本概念

2.1 退化过程数学模型

图像退化可以表示为：

 g(x,y) = h(x,y) * f(x,y) + η(x,y)

其中：👇

f(x,y)：原始清晰图像
h(x,y)：退化函数（点扩散函数PSF）
*：卷积操作
η(x,y)：加性噪声
g(x,y)：观察到的退化图像

类比理解：就像用沾了水的画笔作画，画笔的形状和水分扩散影响了最终画作的效果。

三、线性移不变(LSI)退化模型

3.1 什么是线性移不变系统？

线性性：系统对多个输入的和的响应等于对各输入响应的和
移不变性：系统对平移后的输入的响应等于对原输入响应的平移

1️⃣案例1：手抖拍照 👈
线性： 照片里亮色衣服和暗色裤子模糊程度一致
移不变：整张照片从左到右模糊程度相同
处理： 用统一参数就能修复

线性移不变就是在说：整个图像用一种公平、统一的方式变模糊，这样我们就能用数学公式轻松描述和修复它！

3.2 LSI模型的特点

系统响应与位置无关（均匀退化）
可以通过卷积运算描述
在频域中表现为乘法运算

数学表达：

 G(u,v) = H(u,v)F(u,v) + N(u,v)

其中大写字母表示傅里叶变换后的频域函数

应用实例：

相机对焦不准导致的均匀模糊
大气湍流对天文图像的影响

四、退化函数的估计

4.1 为什么需要估计退化函数？

图像复原需要先知道"图像是如何变差的"，才能"逆向修复"

退化函数又叫做点扩散函数

4.2 估计方法

4.2.1 观察法

从图像中清晰的小点或边缘估计PSF
适用于有已知简单结构的图像

4.2.2 试验估计法

使用相同设备拍摄已知图像（如点光源）
分析得到的退化图像来估计h(x,y)

4.2.3 数学建模法

根据物理过程建立数学模型
如运动模糊、大气湍流等有理论模型

五、平面运动模糊退化模型

——想象你拿着手机边走路边拍照，结果照片拍糊了。这时候如果你知道：
1️⃣ 模糊是怎么产生的（手抖的方向和幅度）
2️⃣ 模糊的数学规律（匀速直线运动造成的拖影）

你就能像侦探一样，通过分析照片的模糊痕迹，逆向还原出清晰的图像！

5.1 模型描述

当相机与被摄物体之间存在相对匀速直线运动时产生的模糊

退化函数：

 h(x,y) = { 1/L, if √(x²+y²) ≤ L/2 且 y/x = tanθ
         { 0, otherwise
其中：

L：运动模糊长度
θ：运动方向角度

5.2 退化案例演示

import cv2
import numpy as np
import matplotlib.pyplot as plt

# -------------------------- 1. 准备测试图像（简单图形，便于观察模糊效果） --------------------------
def create_test_image(size=(256, 256)):
    """创建简单测试图像（含横线、竖线和对角线，便于观察不同方向模糊）"""
    img = np.zeros(size, dtype=np.uint8)
    
    # 添加水平线条（测试垂直模糊效果）
    img[50::40, :] = 255  # 行间隔40像素
    
    # 添加垂直线条（测试-45度模糊效果）
    img[:, 50::40] = 255  # 列间隔40像素
    
    # 添加对角线条（测试两种模糊的综合效果）
    for i in range(0, size[0], 40):
        if i + size[1] < 2*size[0]:
            cv2.line(img, (0, i), (i, 0), 255, 1)
    
    return img

# 创建测试图像（简单图形比自然图像更易观察模糊方向）
# test_image = create_test_image()
test_image = cv2.imread('./img/peppers.bmp', 0) 

# -------------------------- 2. 运动模糊核生成函数 --------------------------
def create_motion_kernel(angle, length):
    """生成指定方向和长度的运动模糊核"""
    angle_rad = np.deg2rad(angle)
    kernel_size = int(np.ceil(length)) + (1 if int(np.ceil(length)) % 2 == 0 else 0)
    kernel = np.zeros((kernel_size, kernel_size), dtype=np.float32)
    center = kernel_size // 2
    
    # 生成运动轨迹
    for i in range(length):
        x = int(center + i * np.cos(angle_rad))
        y = int(center + i * np.sin(angle_rad))
        if 0 <= x < kernel_size and 0 <= y < kernel_size:
            kernel[y, x] += 1
    
    return kernel / np.sum(kernel)  # 归一化

# -------------------------- 3. 创建两种方向的模糊核 --------------------------
# 1. 垂直运动模糊核（方向90度，从上到下）
vertical_kernel = create_motion_kernel(angle=90, length=30)  # 90度=垂直向下  30表示模糊长度，90表示方向，可以修改的，你可以试试

# 2. -45度运动模糊核（从右上到左下）
diagonal_kernel = create_motion_kernel(angle=-45, length=30)  # -45度=右上到左下,0表示模糊长度，-45表示方向，可以修改的，你可以试试

# -------------------------- 4. 应用模糊核退化图像 --------------------------
def apply_blur(image, kernel):
    """对图像应用模糊核"""
    return cv2.filter2D(image, ddepth=-1, kernel=kernel, borderType=cv2.BORDER_REFLECT)

# 生成两种模糊图像
vertical_blur = apply_blur(test_image, vertical_kernel)  # 垂直模糊
diagonal_blur = apply_blur(test_image, diagonal_kernel)  # -45度模糊

# -------------------------- 5. 结果可视化对比 --------------------------
plt.figure(figsize=(15, 10))

# 1. 原始测试图像
plt.subplot(2, 3, 1)
plt.imshow(test_image, cmap='gray')
plt.title('原始测试图像（含横线/竖线/对角线）')
plt.axis('off')

# 2. 垂直模糊核及效果
plt.subplot(2, 3, 2)
plt.imshow(vertical_kernel, cmap='gray')
plt.title('垂直运动模糊核（90度）')
plt.axis('off')

plt.subplot(2, 3, 5)
plt.imshow(vertical_blur, cmap='gray')
plt.title('垂直模糊效果（横线变模糊，竖线清晰）')
plt.axis('off')

# 3. -45度模糊核及效果
plt.subplot(2, 3, 3)
plt.imshow(diagonal_kernel, cmap='gray')
plt.title('-45度运动模糊核')
plt.axis('off')

plt.subplot(2, 3, 6)
plt.imshow(diagonal_blur, cmap='gray')
plt.title('-45度模糊效果（对角线变模糊）')
plt.axis('off')

plt.tight_layout()
plt.show()

# -------------------------- 6. 关键结论 --------------------------
print("\n" + "="*60)
print("运动模糊方向特性分析")
print("="*60)
print("1. 垂直模糊（90度）：")
print("   - 模糊核特点：垂直线状（沿y轴方向）")
print("   - 图像效果：水平线条模糊（沿运动方向扩散），垂直线条保持清晰")

print("\n2. -45度模糊：")
print("   - 模糊核特点：沿-45度方向的线状（从右上到左下）")
print("   - 图像效果：与运动方向一致的对角线模糊，其他方向线条相对清晰")
print("="*60)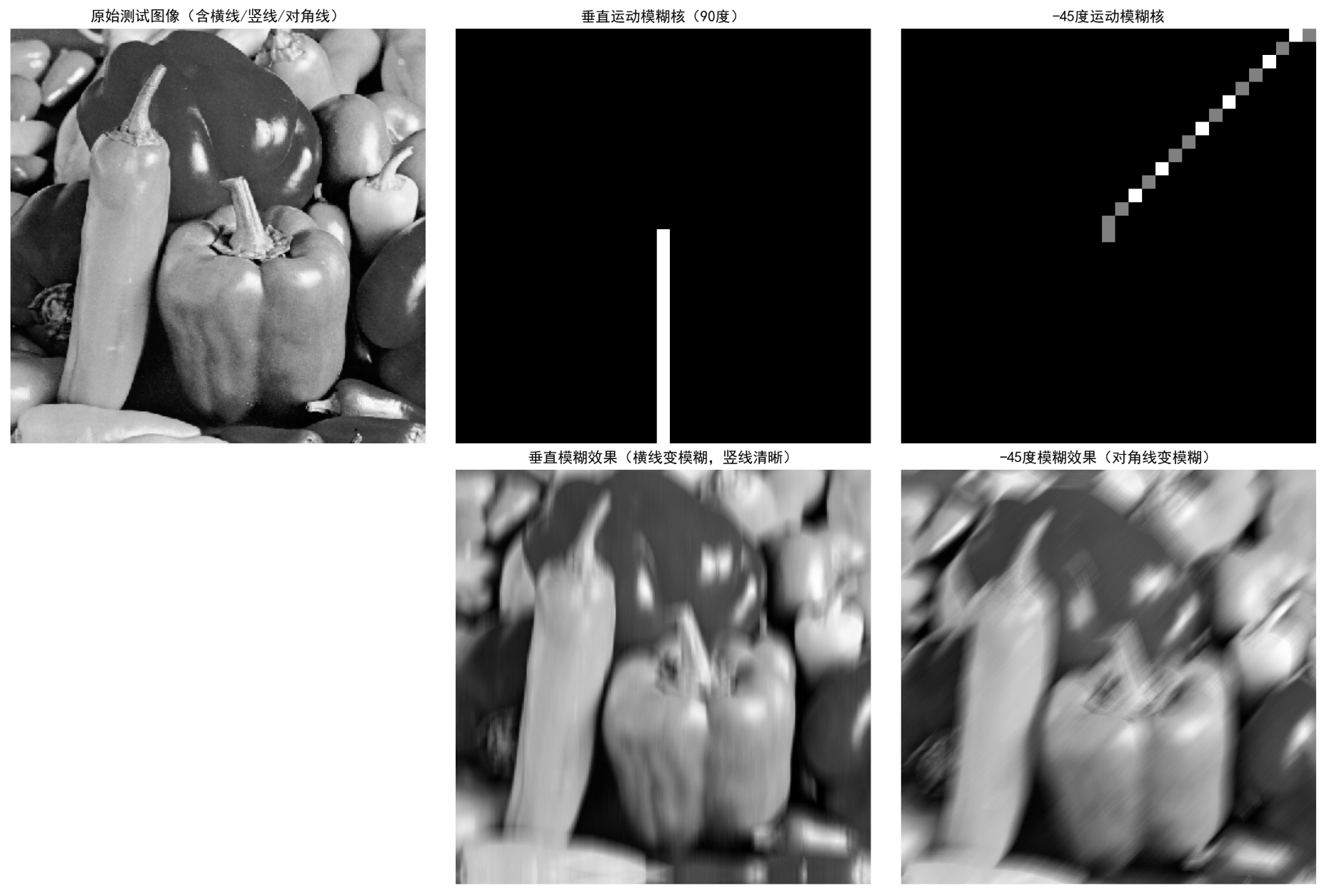

代码解析：

垂直模糊（90度）：
- 模糊核特点：垂直线状（沿y轴方向）
- 图像效果：水平线条模糊（沿运动方向扩散），垂直线条保持清晰
-45度模糊：
- 模糊核特点：沿-45度方向的线状（从右上到左下）
- 图像效果：与运动方向一致的对角线模糊，其他方向线条相对清晰

注意：想象一下，模糊核的结构?

第五章 图像复原

第五章图像复原