第四章 频域图像处理
1. 频率图像平滑
通过本课的学习,学生应该掌握如下知识:
好的,同学们!今天我们学习频域图像处理中最基础也最常用的操作之一:频域图像平滑。频域平滑的核心思想是抑制高频分量,保留低频分量,因为图像的噪声和细节通常对应高频,而缓慢变化的背景和物体大致轮廓对应低频。
我们将重点介绍三种经典的频域低通滤波器:
- 理想低通滤波器 (ILPF)
- 巴特沃斯低通滤波器 (BLPF)
- 高斯低通滤波器 (GLPF)。
空域平滑: 直接对图像像素进行加权平均(如均值滤波、高斯滤波)。
频域平滑:
- 将图像从空域通过傅里叶变换到频域。
- 在频域用低通滤波器 (LPF, Low-Pass Filter) 与频谱相乘,衰减高频分量。
- 通过傅里叶逆变换回到空域,得到平滑图像。
低通滤波器的“传递函数 H(u,v)”, 频域中,滤波器用传递函数 H(u,v) 表示。对于低通滤波器:
- H(u,v) ≈ 1:对于低频分量(靠近频谱中心),允许通过。
- H(u,v) ≈ 0:对于高频分量(远离频谱中心),进行衰减。
关键:频率距离 D(u,v)
所有低通滤波器都基于像素 (u,v) 到频谱中心 (u0, v0) 的欧式距离 D(u,v) 来定义:
D(u,v) = sqrt((u-u0)^2 + (v-v0)^2)通常我们会对频谱进行中心化(fftshift),此时频谱中心为 (M/2, N/2),其中 M, N 是图像尺寸。
1.1 理想低通滤波器
前言
1.1.1 定义
存在一个截止频率 D0, 当 D(u,v) ≤ D0 时,低通滤波器的传递函数 H(u,v) 为 1(表示允许通过),否则为 0(表示衰减)。
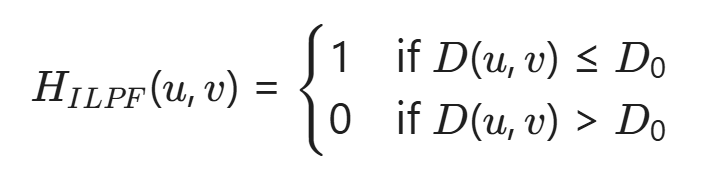
D(u,v)表示从频谱中心到像素 (u,v) 的距离。H(u,v) 表示从像素 (u,v) 到频谱中心的衰减程度。
1.1.2 简单案例:圆形理想低通
想象频谱是一个平面,中心是低频。ILPF 就像一个中心在频谱中心、半径为 D0 的圆。圆内的低频全通过,圆外的高频全挡住
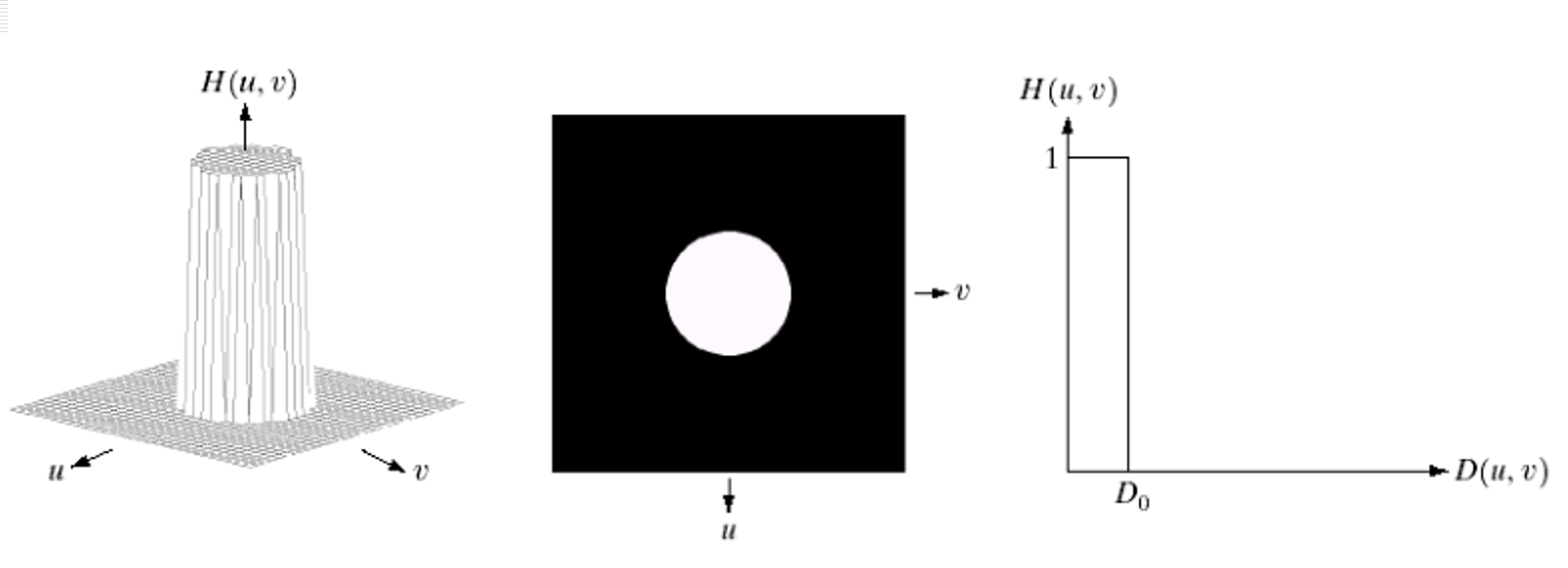

1.1.2 平滑效果与问题:
优点: 理论上能完全保留截止频率内的低频,实现理想平滑。
致命缺点: 振铃效应 (Ringing Artifact)。由于理想阶跃在频域的陡峭截止,逆变换到空域会产生震荡的波纹,导致图像边缘产生模糊的同心圆或波纹。(如下图) 👇
应用场景: 几乎不用于实际图像处理,主要用于理论教学。

总结
课堂作业
- ILPF传递函数中的D0和D(u,v)的物理含义?
- 理想低通滤波器存在什么问题?
- 对于理想低通常滤波器,如何优化它?
1.2 巴特沃斯低通滤波器
前言
1.2.1 什么是巴特沃斯滤波器?
巴特沃斯滤波器的传递函数是平滑过渡的,没有理想滤波器的陡峭截止。其阶数 n 控制过渡的陡峭程度。
一个n 阶巴特沃斯低通滤波器的传递函数为:
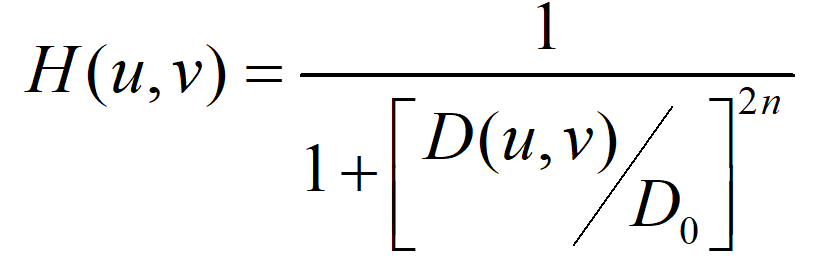
D0 是截止频率,当 D(u,v)=D0时,H=1/(1+1)=0.5(衰减一半功率)。
n 是阶数,n 越大,过渡越陡峭,越接近理想滤波器;n 越小,过渡越平缓,其尾部保留有一些高频信息。 见下图👇

D(u,v)表示从频谱中心到像素 (u,v) 的距离。H(u,v) 表示从像素 (u,v) 到频谱中心的衰减程度。
1.2.1简单案例:不同阶数的BLPF
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负
def BLPF(fshift,D0,n): # 巴特沃斯低通滤波器
rows,cols=fshift.shape
crow,ccol=rows//2,cols//2
H=np.zeros((rows,cols))
for u in range(rows):
for v in range(cols):
D=np.sqrt((u-crow)**2+(v-ccol)**2)
H[u,v]=1/(1+(D/D0)**(2*n))
fshift1=fshift*H
return fshift1,H
img=cv.imread(r'./img/achip.tif',0)
f=np.fft.fft2(img) # 傅里叶变换
fshift=np.fft.fftshift(f)
magnitude_spectrum=20*np.log(1+np.abs(fshift)) # 幅度谱
angle_spectrum=np.abs(np.angle(fshift))
fshift1,H=BLPF(fshift,30,2) # 巴特沃斯低通滤波器 30表示截止频率,2表示阶数 <=你可以改这个参数哦
f_ishift=np.fft.ifftshift(fshift1)
img_back=np.fft.ifft2(f_ishift)
img_back=np.abs(img_back)
plt.figure(figsize=(10,5))
plt.subplot(151),plt.imshow(img, cmap = 'gray') #显示加噪图像
plt.title('原图像'), plt.axis("off")
plt.subplot(152),plt.imshow(magnitude_spectrum, cmap = 'gray') #显示加噪图像
plt.title('原幅值谱')
plt.axis("off")
plt.subplot(153),plt.imshow(H, cmap = 'gray')
plt.title('巴特沃斯传递函数'), plt.axis("off")
plt.subplot(154),plt.imshow(20*np.log(1+np.abs(fshift1)), cmap = 'gray') #显示加噪图像
plt.title('滤波后的幅值谱')
plt.axis("off")
plt.subplot(155),plt.imshow(img_back, cmap = 'gray') #显示加噪图像
plt.title('重构图像')
plt.axis("off")
plt.show()
1.2.3 平滑效果与特点:
优点:振铃效应远小于理想滤波器。阶数 n可调节,灵活性高。
缺点:当阶数较高时,仍会有轻微振铃效应。见下图👇
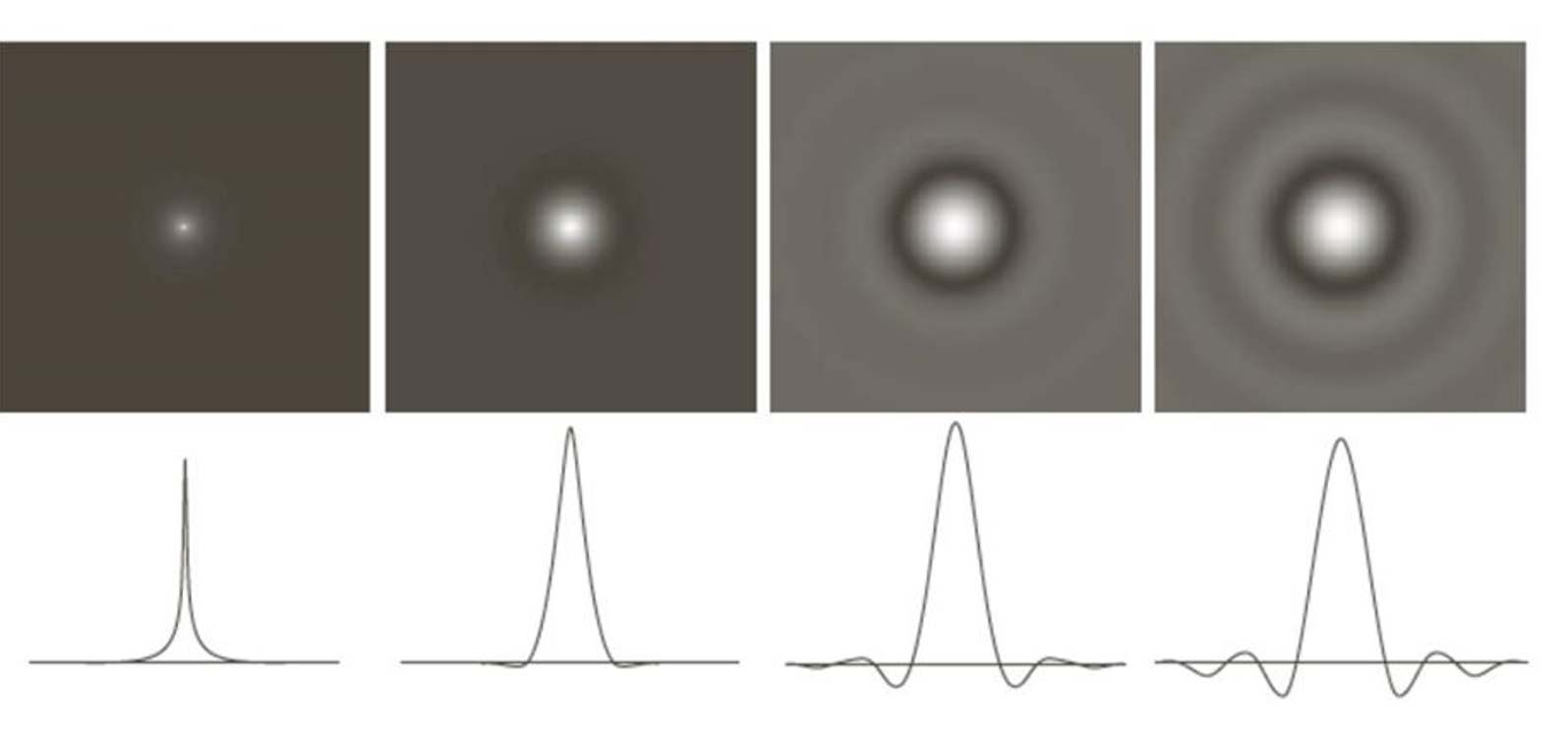
1.3 高斯低通滤波器
前言
1.3.1 什么是高斯滤波器?
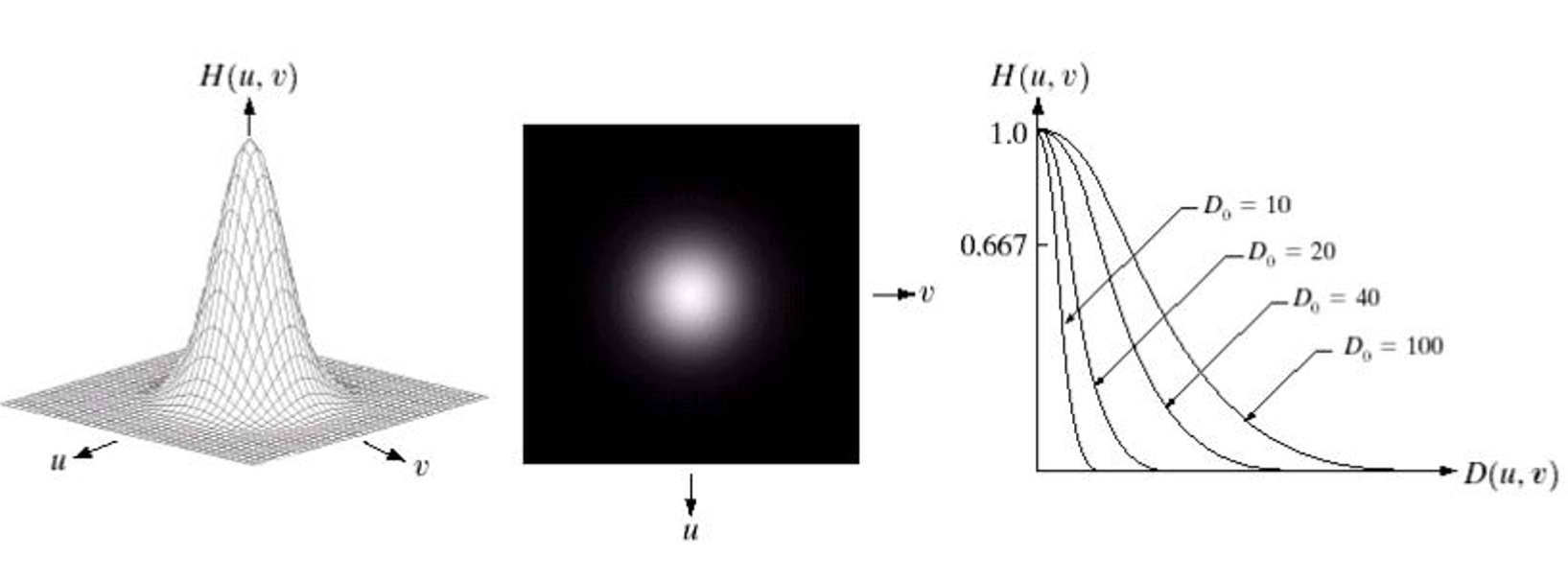
高斯低通滤波器的传递函数是高斯函数,具有最平滑的过渡,且其傅里叶变换仍是高斯函数,在空域不会产生振铃效应。
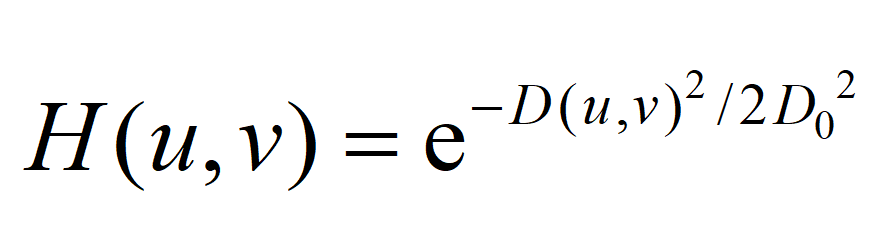
σ:高斯函数的标准差,控制滤波器的宽度(平滑程度)。σ 越大,高频衰减越少,图像越清晰;σ 越小,高频衰减越多,图像越模糊。

1.3.2 简单案例,三种滤波器对比
import cv2
import numpy as np
import matplotlib.pyplot as plt
# ---------------------- 1. 定义滤波器生成函数 (修正关键!) ----------------------
def ideal_lpf(M, N, D0):
"""生成理想低通滤波器,确保尺寸为 M (高度) × N (宽度)"""
u = np.arange(M) # 行索引 (高度方向),范围 [0, M-1]
v = np.arange(N) # 列索引 (宽度方向),范围 [0, N-1]
u, v = np.meshgrid(u, v, indexing='ij') # 生成网格,注意用 'ij' 索引确保 u 对应行,v 对应列
center_u, center_v = M // 2, N // 2 # 频谱中心 (行数中心, 列数中心)
D = np.sqrt((u - center_u)**2 + (v - center_v)** 2) # 频率距离
H = (D <= D0).astype(float) # 理想低通:D <= D0 时为 1,否则为 0
return H
def butterworth_lpf(M, N, D0, n):
"""生成巴特沃斯低通滤波器"""
u = np.arange(M)
v = np.arange(N)
u, v = np.meshgrid(u, v, indexing='ij')
center_u, center_v = M // 2, N // 2
D = np.sqrt((u - center_u)**2 + (v - center_v)** 2)
H = 1 / (1 + (D / D0)**(2 * n)) # 巴特沃斯公式
return H
def gaussian_lpf(M, N, sigma):
"""生成高斯低通滤波器"""
u = np.arange(M)
v = np.arange(N)
u, v = np.meshgrid(u, v, indexing='ij')
center_u, center_v = M // 2, N // 2
D_sq = (u - center_u)**2 + (v - center_v)** 2 # 距离的平方
H = np.exp(-D_sq / (2 * sigma**2)) # 高斯公式
return H
# ---------------------- 2. 频域平滑函数 (保持不变) ----------------------
def func1(img_gray, H):
# 傅里叶变换
fft = np.fft.fft2(img_gray) # 结果形状: (M, N),与图像一致
fft_shift = np.fft.fftshift(fft) # 频谱中心化,形状仍为 (M, N)
# 频域滤波 (相乘):此时 H 的形状也是 (M, N),可正常相乘
fft_filtered = fft_shift * H
# 逆傅里叶变换
ifft_shift = np.fft.ifftshift(fft_filtered)
img_filtered = np.fft.ifft2(ifft_shift).real # 取实部(消除数值误差)
return np.clip(img_filtered, 0, 255).astype(np.uint8) # 确保像素值在 [0,255]
# ---------------------- 3. 主程序 ----------------------
# 读取图像并转为灰度图
img = cv2.imread('./img/achip.tif')
if img is None:
raise FileNotFoundError("错误:未找到 'food.jpg',请检查路径是否正确!")
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 转为灰度图
M, N = img_gray.shape # 获取图像尺寸:M (高度) × N (宽度)
print(f"图像尺寸:高度 M={M}, 宽度 N={N}") # 打印尺寸,确认滤波器是否匹配
# 设计三种滤波器 (参数匹配平滑程度,尺寸与图像一致:M×N)
D0 = 30 # 截止频率(控制平滑程度,值越小越模糊)
H_ilpf = ideal_lpf(M, N, D0) # 理想低通滤波器,形状 (M, N)
H_blpf = butterworth_lpf(M, N, D0, n=2) # 巴特沃斯低通滤波器,阶数 n=2
H_glpf = gaussian_lpf(M, N, sigma=20) # 高斯低通滤波器,sigma=20
# 频域平滑
img_ilpf = func1(img_gray, H_ilpf) # 理想低通滤波结果
img_blpf = func1(img_gray, H_blpf) # 巴特沃斯低通滤波结果
img_glpf = func1(img_gray, H_glpf) # 高斯低通滤波结果
# ---------------------- 4. 显示结果 ----------------------
plt.figure(figsize=(18, 12))
plt.subplot(221), plt.imshow(img_gray, cmap='gray'), plt.title('原图'), plt.axis('off')
plt.subplot(222), plt.imshow(img_ilpf, cmap='gray'), plt.title('理想低通滤波 (振铃严重)'), plt.axis('off')
plt.subplot(223), plt.imshow(img_blpf, cmap='gray'), plt.title('巴特沃斯低通滤波 (n=2)'), plt.axis('off')
plt.subplot(224), plt.imshow(img_glpf, cmap='gray'), plt.title('高斯低通滤波 (σ=20)'), plt.axis('off')
plt.tight_layout()
plt.show()
结果解读:👇
- 原图
- 理想低通滤波:模糊且边缘有明显振铃效应(同心圆波纹)
- 巴特沃斯低通滤波:模糊,振铃效应明显减轻(阶数 n=2 时接近无振铃)
- 高斯低通滤波:模糊,完全无振铃,效果最自然
1.3.3 平滑效果与特点:
优点:完全无振铃效应(因为高斯函数的傅里叶变换仍是高斯函数,空域也是平滑的) 。过渡非常平滑,结果自然。
缺点 :相比同阶巴特沃斯滤波器,需要更大的 D0才能达到相同的平滑效果
应用场景 :实际图像处理中的首选低通滤波器之一,尤其适用于对平滑效果要求高、不希望有振铃的场景(如医学图像、遥感图像)。
2. 频率图像锐化
相关信息
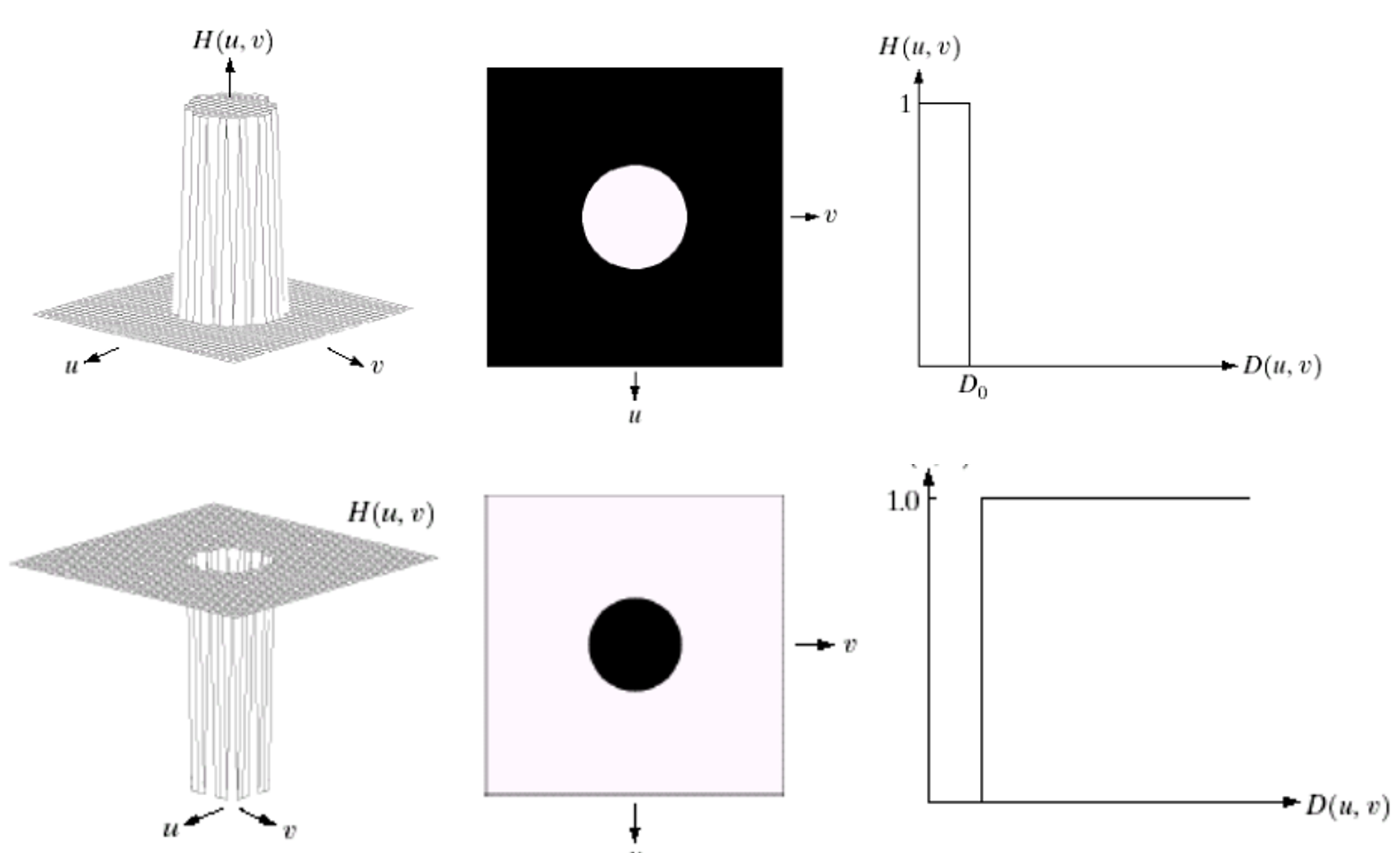
高通滤波就是让高频分量通过, 并抑制低频分量, 从而增强图像中的高频成分, 使图像的边缘或线条变得清晰, 达到图像的锐化的目的。
图像锐化相当于从原图像中减去图像的平滑部分,因此高通滤波器与低通滤波器的传递函数存在以下关系:
H(u,v)=1-L(u,v),其中L(u,v)是低通滤波器的传递函数。
2.1 理想高通滤波器
前言
2.1.1 什么是理想高通滤波器?
与理想低通滤波器相反,存在截止频率 D0,频率距离 D(u,v)≥D0 的高频分量全部通过,否则全部滤除。

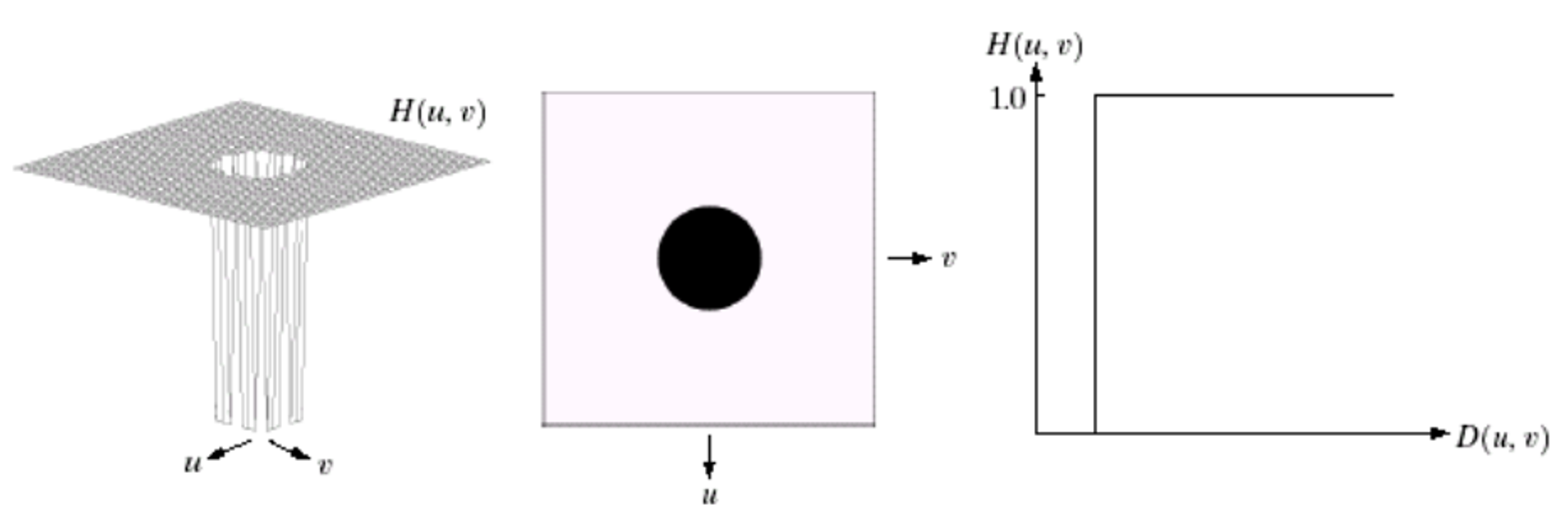
2.1.2 巴特沃斯高通滤波器
与 巴特沃斯低通滤波器 的定义是一致的,只不过是把 低通滤波器 的 1 换成 0 , 0 换成 1 。
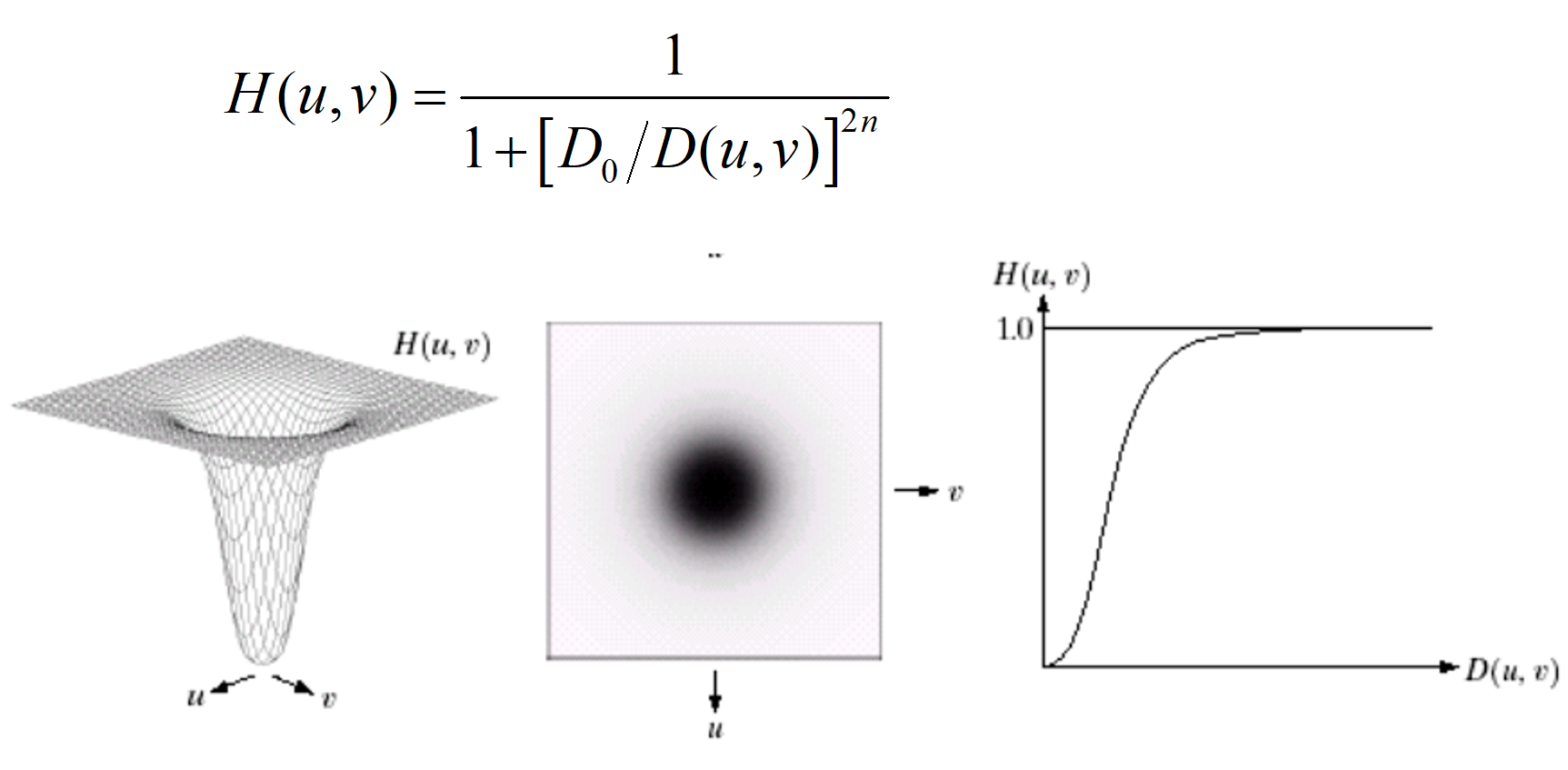
2.1.3 高斯高通滤波器
高斯高通滤波器的传递函数如下: 👇
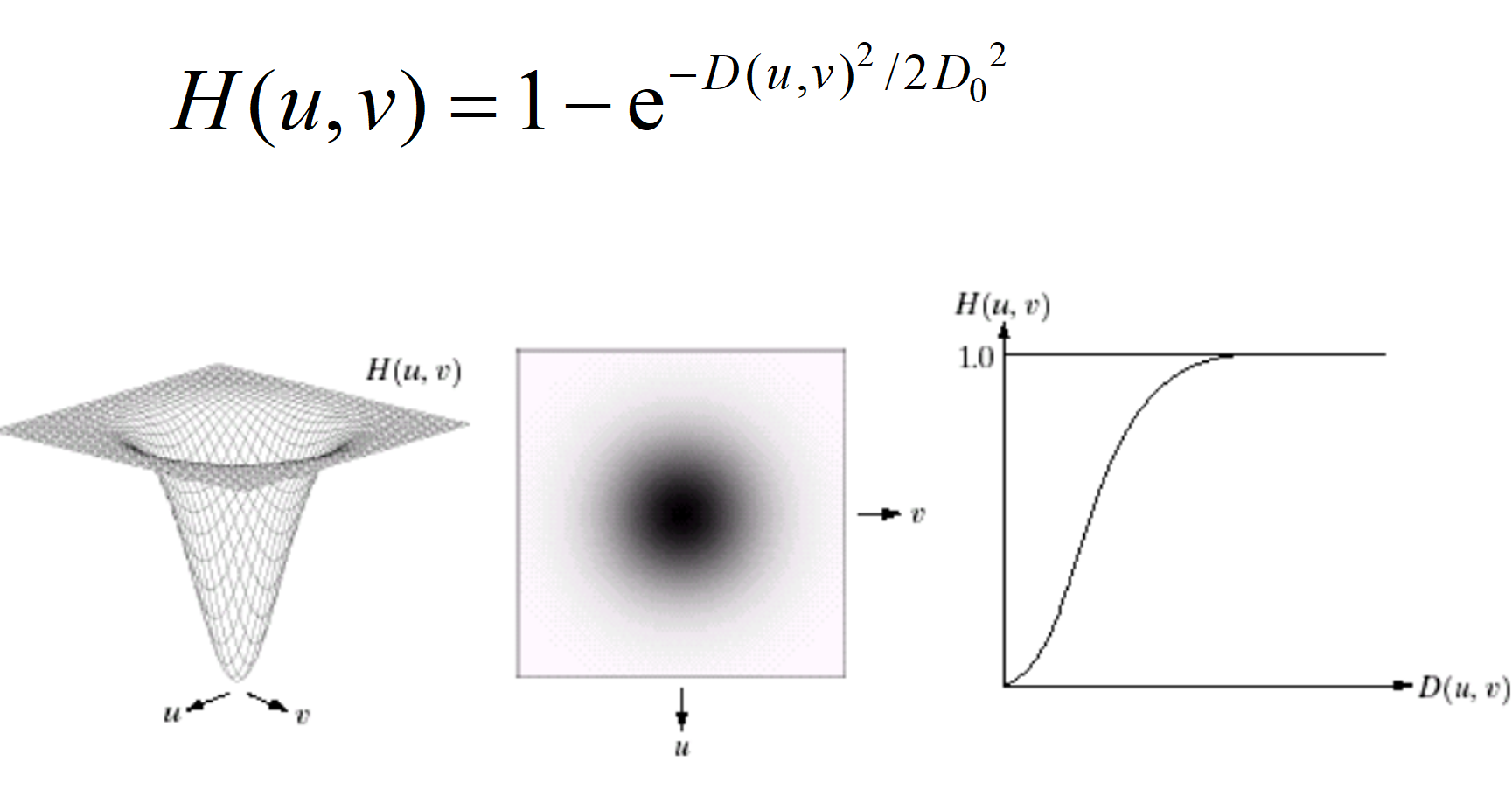
2.1.4 简单案例,三种滤波器对比
import cv2
import numpy as np
import matplotlib.pyplot as plt
# ---------------------- 1. 高通滤波器生成函数 ----------------------
def ideal_hpf(M, N, D0):
u = np.arange(M)
v = np.arange(N)
u, v = np.meshgrid(u, v, indexing='ij')
center_u, center_v = M//2, N//2
D = np.sqrt((u - center_u)**2 + (v - center_v)** 2)
H = (D > D0).astype(float)
return H
def butterworth_hpf(M, N, D0, n):
u = np.arange(M)
v = np.arange(N)
u, v = np.meshgrid(u, v, indexing='ij')
center_u, center_v = M//2, N//2
D = np.sqrt((u - center_u)**2 + (v - center_v)** 2)
D = np.where(D == 0, 1e-10, D) # 避免除零
H = 1 / (1 + (D0 / D)**(2 * n))
return H
def gaussian_hpf(M, N, sigma):
u = np.arange(M)
v = np.arange(N)
u, v = np.meshgrid(u, v, indexing='ij')
center_u, center_v = M//2, N//2
D_sq = (u - center_u)**2 + (v - center_v)** 2
H = 1 - np.exp(-D_sq / (2 * sigma**2))
return H
# ---------------------- 2. 频域锐化函数 ----------------------
def func2(img_gray, H):
# 傅里叶变换
fft = np.fft.fft2(img_gray)
fft_shift = np.fft.fftshift(fft) # 频谱中心化
# 频域滤波 (相乘)
fft_filtered = fft_shift * H
# 逆傅里叶变换
ifft_shift = np.fft.ifftshift(fft_filtered)
img_filtered = np.fft.ifft2(ifft_shift).real # 取实部
return np.clip(img_filtered, 0, 255).astype(np.uint8) # 确保像素值合法
# ---------------------- 3. 主程序 ----------------------
# 读取图像并转为灰度图
img = cv2.imread('./img/moon.jpg')
if img is None:
raise FileNotFoundError("未找到 'food.jpg',请检查路径!")
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
M, N = img_gray.shape # 获取图像尺寸 M×N
# 设计三种高通滤波器 (参数尽量匹配锐化程度)
D0 = 30
H_ihpf = ideal_hpf(M, N, D0)
H_bhpf = butterworth_hpf(M, N, D0, n=2) # 阶数 n=2
H_ghpf = gaussian_hpf(M, N, sigma=20) # sigma=20 对应 D0≈30
# 频域锐化
img_ihpf = func2(img_gray, H_ihpf)
img_bhpf = func2(img_gray, H_bhpf)
img_ghpf = func2(img_gray, H_ghpf)
# ---------------------- 4. 显示结果 ----------------------
plt.figure(figsize=(18, 12))
plt.subplot(221), plt.imshow(img_gray, cmap='gray'), plt.title('原图'), plt.axis('off')
plt.subplot(222), plt.imshow(img_ihpf, cmap='gray'), plt.title('理想高通滤波 (振铃严重)'), plt.axis('off')
plt.subplot(223), plt.imshow(img_bhpf, cmap='gray'), plt.title('巴特沃斯高通滤波 (n=2)'), plt.axis('off')
plt.subplot(224), plt.imshow(img_ghpf, cmap='gray'), plt.title('高斯高通滤波 (σ=20)'), plt.axis('off')
plt.tight_layout()
plt.show()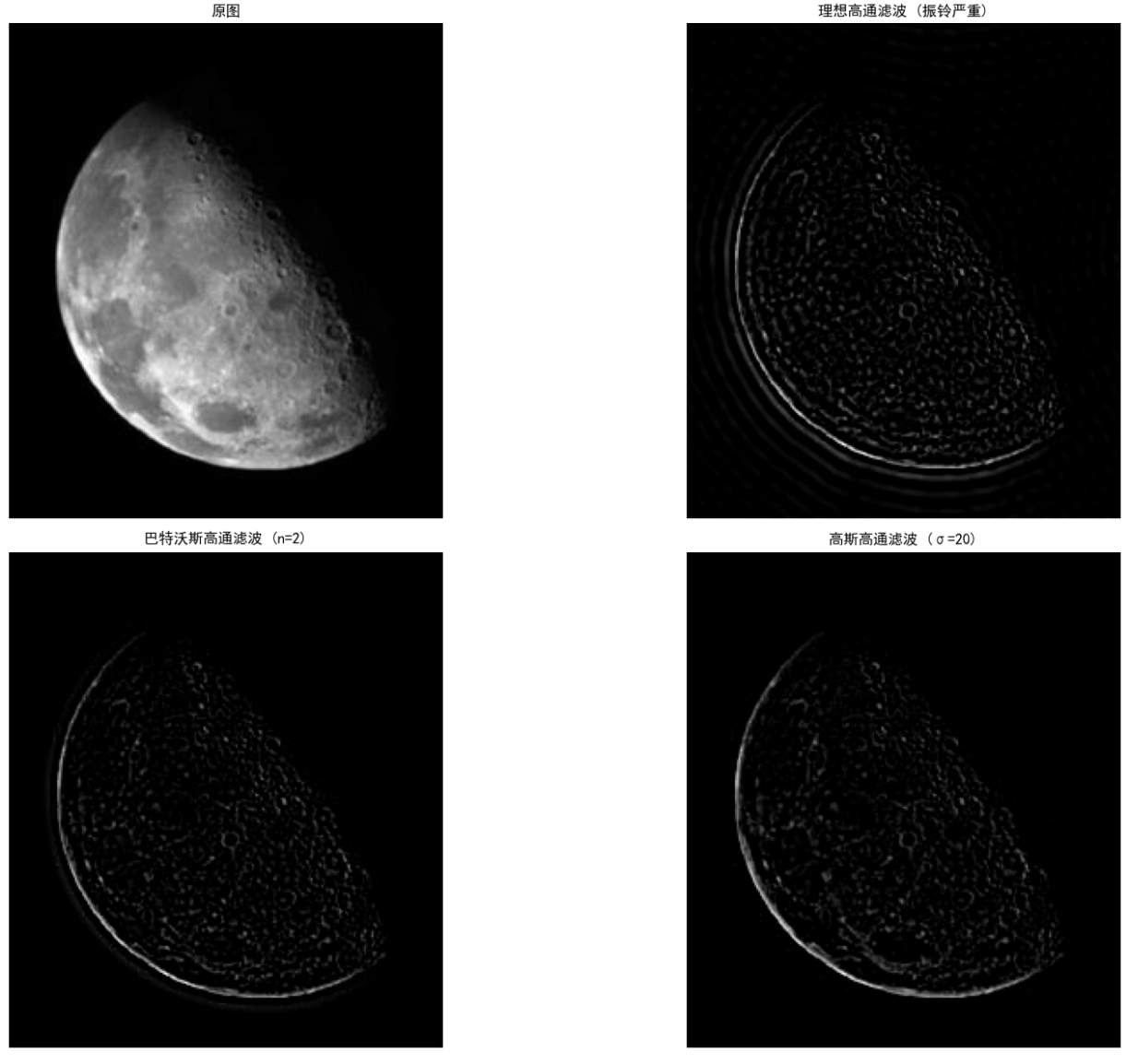
效果预期:
- IHPF:边缘和细节增强,但振铃效应严重(边缘周围有波纹)。
- BHPF:边缘增强,振铃效应轻微,细节清晰。
- GHPF:边缘和细节自然增强,完全无振铃,锐化效果最柔和自然。
2.1.5 选择建议:
追求无振铃、自然锐化 → 高斯高通滤波器(实际应用首选)。
需要更强锐化且能接受轻微振铃 → 巴特沃斯高通滤波器(阶数n=2∼4)。
理论演示 → 理想高通滤波器。
记住 :高通滤波会增强噪声(因为噪声也是高频),因此实际应用中常先对图像进行平滑去噪,再进行锐化。
2.4 空滤波波和频域滤波的关系
前言
空滤平滑相当于频域滤波的低通滤波,频域锐化相当于频域滤波的高通滤波。
2.5 案例
1 直接操作频谱图
前言
import cv2
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
# 读取图像并转换为灰度图
img = cv2.imread(r'./img/peppers.bmp',0)
# 对图像进行二维傅里叶变换
F = np.fft.fft2(img)
# 将频谱的零频率分量移到频谱中心
fshift0 = np.fft.fftshift(F)
# 创建频谱的副本用于修改
G = fshift0.copy()
# 获取频谱的最大幅值
fmax = np.max(np.abs(fshift0))
# 获取图像尺寸
m, n = F.shape
# 计算图像中心坐标
u0, v0 = m//2, n//2 # 图像中心
# 第一组频率点:在水平方向上偏移
r1 = 50
u1 = u0
v1 = v0 - r1 # 中心上方50像素
G[u1, v1] = fmax/5 # 设置该频率点的幅值为最大值的1/5
# 设置对称点(根据傅里叶变换的对称性)
u2 = m - 1 - u1
v2 = n - 1 - v1
G[u2, v2] = fmax/5
# 第二组频率点:在对角线方向上偏移
r1 = 5
u1 = u0 + r1
v1 = v0 + r1 # 中心右下方5像素
G[u1, v1] = fmax/2 # 设置该频率点的幅值为最大值的1/2
# 设置对称点
u2 = m - 1 - u1
v2 = n - 1 - v1
G[u2, v2] = fmax/2
# 创建显示窗口
plt.figure(figsize=(20, 10))
# 显示修改后的频谱(使用对数变换增强可视化效果)
plt.subplot(121)
plt.imshow(20*np.log(1+abs(G)), cmap='gray')
plt.title('修改后的频谱')
# 逆变换:将频谱移回原始位置
f1 = np.fft.ifftshift(G)
# 逆傅里叶变换重构图像
img1 = abs(np.fft.ifft2(f1))
# 显示重构后的图像
plt.subplot(122)
plt.imshow(img1, cmap='gray')
plt.title('重构图像')
# 保存图像img1
cv2.imwrite('./img/peppers_new.jpg', img1)
plt.show()结果解析: 👇
左侧图像(修改后的频谱):
- 显示的是经过修改的频域图像
- 在对数尺度下显示,便于观察不同强度的频率分量
- 可以看到四个明显的亮点:
- 中心的大亮区域:代表图像的低频成分(主要结构信息)
- 上下对称的两个较暗亮点:位于垂直方向上距离中心50像素处
- 对角线对称的两个较亮亮点:位于中心右下方5像素处及其对称点
右侧图像(重构图像):
- 这是将修改后的频谱通过逆傅里叶变换重构得到的图像
- 由于在频域中人为添加了特定的频率分量,重构图像会出现相应的周期性模式
频域操作的效果:
- 添加的频率分量:在频域特定位置增强了幅值
- 对称性:由于实图像的傅里叶变换具有共轭对称性,修改时必须同时修改对称点
- 视觉效果:在空间域中,这些频域修改会表现为:
- 垂直方向的频率分量 → 水平方向的条纹模式
- 对角线方向的频率分量 → 特定角度的周期性模式

2. 实验三的第二题的代码
前言
教材后面226页,实验三的第二题的代码,代码是不完全的,需要完善空余的部分,才可以运行。
import cv2
import numpy as np
import matplotlib.pyplot as plt
def addGaussianNoise(src, means, sigma):
NoiseImg = src.copy() # 修正:需要复制原图像,避免修改原数据
rows = NoiseImg.shape[0]
cols = NoiseImg.shape[1]
for i in range(rows):
for j in range(cols):
# Python 里使用 random.gauss 函数加高斯噪声
NoiseImg[i, j] = NoiseImg[i, j] + np.random.normal(means, sigma) # 修正:random.gauss 改为 np.random.normal(更常用)
if NoiseImg[i, j] < 0:
NoiseImg[i, j] = 0
elif NoiseImg[i, j] > 1:
NoiseImg[i, j] = 1
return NoiseImg
# 读取图像(替换为你的图像路径)
img0 = cv2.imread( )
img0 = img0 / 255.0 # 归一化到0-1范围(适配噪声处理)
# 添加高斯噪声(means设为0,sigma设为0.1,可根据需求调整)
img = addGaussianNoise( )
# 对加噪图像做傅里叶变换
f = np.fft.fft2( )
# 将频域低频移到中心
fshift = np.fft.fftshift( )
# 计算加噪图像的频域幅度谱(用于显示)
magnitude_spectrum0 = 20 * np.log(1 + np.abs( ))
# 显示加噪图像和其频域幅度谱
plt.figure(figsize=(10, 5))
# 显示加噪图像
plt.subplot(141)
plt.imshow(img, cmap='gray')
plt.title('噪声图像'), plt.axis('off')
# 显示加噪图像频域谱
plt.subplot(142)
plt.imshow( , cmap='gray')
plt.title('噪声图像幅值谱'), plt.axis('off')
# 进行理想低通滤波
r = # 截止频率(可根据需求调整)
m, n = fshift.shape
H = np.zeros((m, n)) # 创建滤波模板
for i in range(m):
for j in range(n):
# 计算当前点到频域中心的距离
d = np.sqrt((i - m/2) ** 2 + (j - n/2) ** 2)
if d <= r:
H[i, j] = # 理想低通:截止频率内保留(设为1)
# 频域滤波(频域图 × 滤波模板)
G =
# 计算滤波后的频域幅度谱
magnitude_spectrum1 = 20 * np.log(1 + np.abs(G))
# 逆傅里叶变换(频域转空域)
f1 = np.fft.ifftshift(G)
img_filtered = np.fft.ifft2(f1).real # 取实部(去除虚部误差)
# 显示滤波后的频域谱和滤波后图像(可补充到plt中)
plt.subplot(143)
plt.imshow(magnitude_spectrum1, cmap='gray')
plt.title('滤波后幅值谱'), plt.axis('off')
plt.subplot(144)
plt.imshow(img_filtered, cmap='gray')
plt.title('滤波后图像'), plt.axis('off')
plt.show()
