第四章 频域图像处理
傅里叶变换的性质
相关信息
同学们,大家好!今天我们要进入一个稍微高级 一点,但又极其重要的领域——数字图像的傅里叶变换性质。别怕,我们从“零基础”出发,用最简单的语言和案例来理解这些看似抽象的概念。
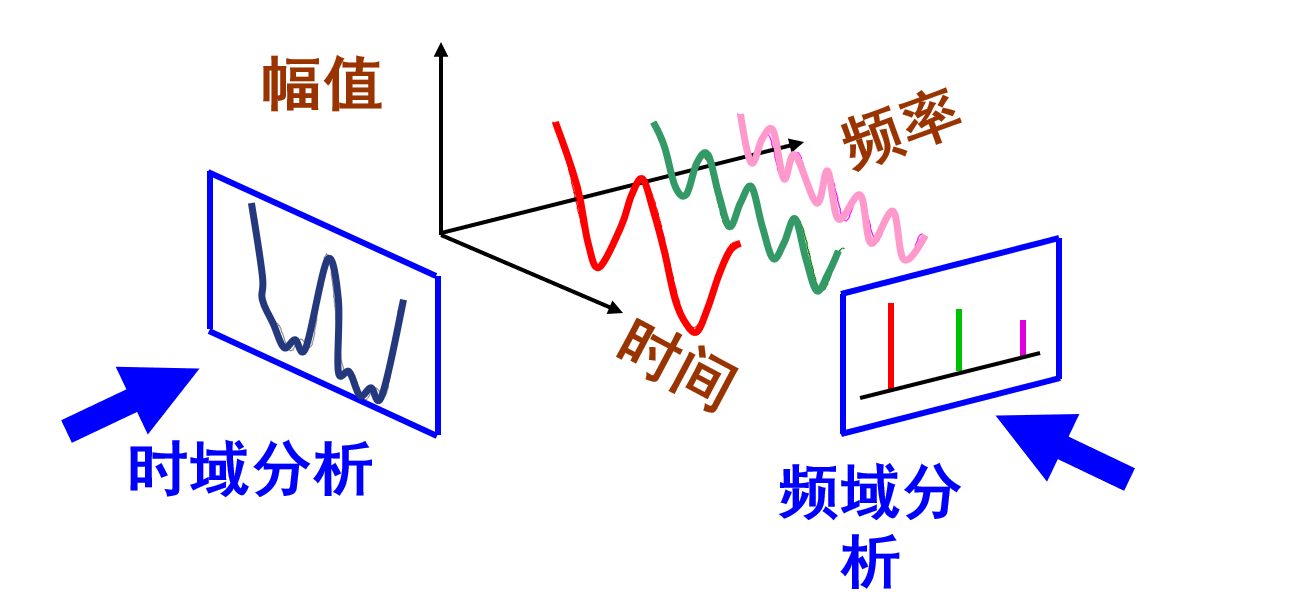
我们知道,傅里叶变换把图像从“空域”(我们看到的一个个像素)转换到了“频域”(如下图👇)。空域研究的哪里有灰度变化,而频域研究的是灰度变化有多快。变化快 的就是高频 信息(边缘、细节、噪声),变化慢 的就是低频 信息(平缓区域、大色块)。
理解了频域,我们就能更好地进行滤波(比如平滑去噪、锐化增强)。而要熟练运用频域,就必须掌握傅里叶变换的几个核心性质。
1. 可分离性
前言
1. 什么是可分离性?
简单说:一个复杂的二维操作,可以分解成两个简单的一维操作。
2. 简单案例:像搭积木 👇\
想象你要计算一个 3x3 图像的 2D DFT。
1️⃣ 方法一(直接算):直接对9个像素进行双重求和,计算量大。
2️⃣ 方法二(利用可分离性):
- 先对3行,每行3个像素,各做一次1D DFT,得到3行新数据(每行是1D DFT结果)。
- 再对这3行新数据的每一列(共3列),各做一次1D DFT,得到最终的2D DFT结果。
好处:大大减少了计算量! 👍
3. 离散傅里叶变换的可分离性
离散傅里叶变换可以用可分离的形式表示:
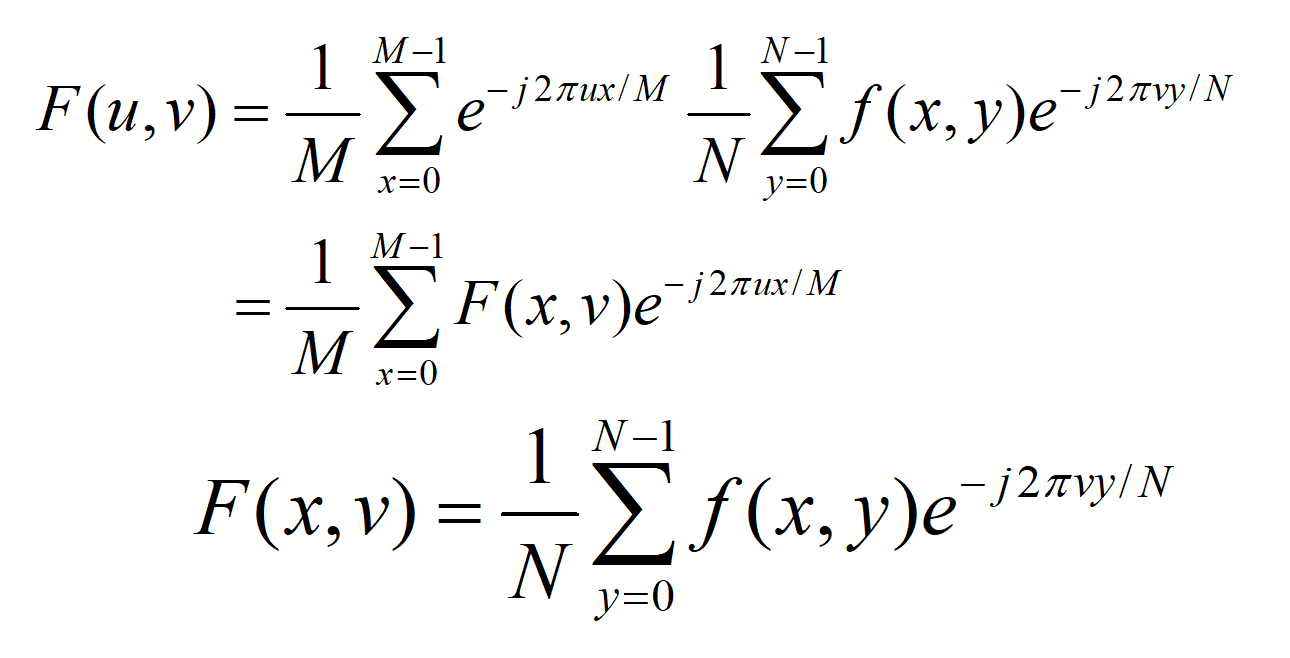
第一步:固定图像的X坐标,对图像的每一列求一维傅里叶变换,对每一个y值(此时x表示常量),求一维傅里叶变换。(公式2)
第二步:对F(x,v)的每一行(此时y表示常量),求一维傅里叶变换, 这样将一个二维傅里叶变换分解为两个一维傅里叶变换。(公式1)

4. 案例演示
准备图片素材
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 设置中文显示
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负
# 读取图像 (确保 food.jpg 与 notebook 在同一目录,或使用绝对路径)
img = cv2.imread('./img/peppers.bmp')
if img is None:
raise FileNotFoundError("请确保 'peppers.bmp' 文件存在于当前工作目录!")
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 转为灰度图,简化处理
M, N = img_gray.shape # 获取图像尺寸
# 定义一个显示函数,方便显示原图和频谱图
def show_images(images, titles, figsize=(15, 10)):
plt.figure(figsize=figsize)
for i, (img, title) in enumerate(zip(images, titles)):
plt.subplot(1, len(images), i+1) # 1行len(images)列,第i+1个
plt.imshow(img, cmap='gray') # 灰度图
plt.title(title)
plt.axis('off')
plt.tight_layout() # 调整子图间距
plt.show() # 显示图像演示傅里叶变换的可分离性
# 方法1: 直接调用 numpy 的 2D FFT
fft2 = np.fft.fft2(img_gray)
# 方法2: 利用可分离性,先对每行做1D FFT,再对每列做1D FFT
fft_rows = np.fft.fft(img_gray, axis=1) # 对每行做1D FFT
fft_sep = np.fft.fft(fft_rows, axis=0) # 对结果的每列做1D FFT
# 比较两种方法的结果差异 (理论上应完全相同,数值误差可忽略)
max_diff = np.max(np.abs(fft2 - fft_sep))
print(f"两种方法结果的最大差异: {max_diff:.2e}") # 非常小,接近机器精度
# 显示频谱中心化后的幅度谱 (为了可视化)
def fft_show(fft_img, title):
fft_shift = np.fft.fftshift(fft_img) # 频谱中心化
magnitude_spectrum = 20 * np.log(np.abs(fft_shift) + 1) # 取对数,增强可视性
plt.imshow(magnitude_spectrum, cmap='gray')
plt.title(title)
plt.axis('off')
plt.figure(figsize=(12, 6))
plt.subplot(121)
fft_show(fft2, '直接 2D FFT 频谱')
plt.subplot(122)
fft_show(fft_sep, '分离式 1D FFT + 1D FFT 频谱')
plt.tight_layout()
plt.show()
print("\n结论:两种方法得到的频谱几乎完全一致,验证了可分离性。")
print("实际应用:计算机内部都是用分离式计算来加速 2D FFT。")结果:

两种方法结果的最大差异: 0.00e+00
5. 应用场景
算法实现:所有傅里叶变换的软件(如MATLAB、OpenCV)都利用了可分离性来加速计算。如果没有可分离性,实时处理图像几乎不可能。
2. 共轭对称性
共轭对称性
1. 什么是共轭对称性?
对于一个实信号(我们的数字图像,像素值都是实数),其傅里叶变换 F(u,v) 具有共轭对称性。
数学描述:
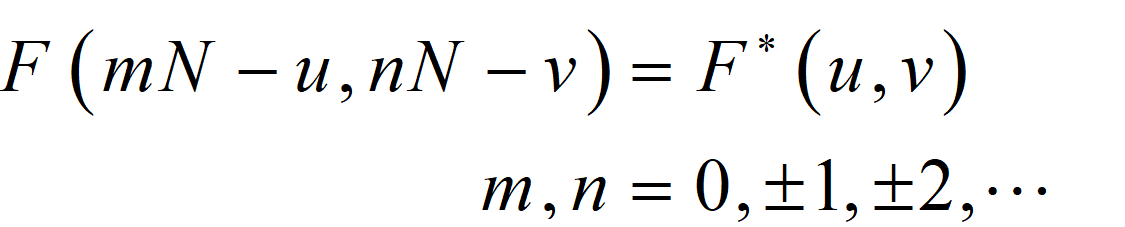
∗ 表示复数共轭(实部相同,虚部相反)。
2. 直观理解:“镜像对称”
对于实图像,其傅里叶变换的幅度谱(频谱图) 关于原点对称 。
也就是说,如果你把频谱图旋转180度,它看起来和原来一样。 幅度谱:∣F(N-u,N-v)∣=∣F(u,v)∣

3. 案例演示
# 计算灰度图(实信号)的 FFT
fft2 = np.fft.fft2(img_gray)
# 不进行中心化的幅度谱
magnitude_raw = np.abs(fft2) # 取幅度
magnitude_raw_log = 20 * np.log(magnitude_raw + 1) # 取对数,增强可视性
# 进行中心化的幅度谱 (将原点移到中心,更直观展示对称性)
fft_shift = np.fft.fftshift(fft2) # 将原点移到中心
magnitude_centered = np.abs(fft_shift) # 取幅度
magnitude_centered_log = 20 * np.log(magnitude_centered + 1) # 取对数,增强可视性
show_images(
[magnitude_raw_log, magnitude_centered_log],
['原始频谱 (未中心化) - 对称中心在角落', '中心化频谱 - 对称中心在图像中心']
)
print("\n观察:中心化后的频谱图,左右、上下都呈现明显的对称性。")
print("结论:实图像的傅里叶变换幅度谱具有共轭对称性。")
print("应用:只需存储一半频谱数据,节省存储空间。")
观察 :中心化后的频谱图,左右、上下都呈现明显的对称性。
结论 :实图像的傅里叶变换幅度谱具有共轭对称性。
应用 :只需存储一半频谱数据,节省存储空间。
4. 应用场景
数据存储 :由于对称性,我们只需要存储一半的数据就可以了,节省存储空间。
频谱图观察 :在显示频谱图时,我们通常会做“频谱中心化”(将低频分量移到中心),这就是利用了共轭对称性,让对称模式更直观。
说明:为什么要取对数? 👇
magnitude_centered_log = 20 * np.log(magnitude_centered + 1) # 取对数,增强可视性傅里叶变换的幅度谱(频谱图)的值范围通常很大,直接显示时,数值差异不明显,取对数后,频谱图更清晰,便于观察。
3. 周期性
周期性
1. 什么是周期性?
离散傅里叶变换及其逆变换具有周期N的周期性:
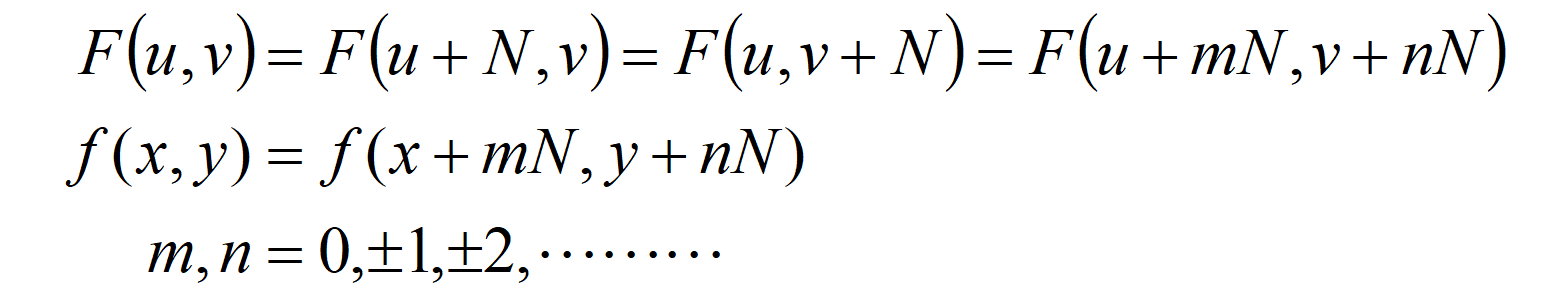
2. 简单案例:时域周期延拓
当我们对一幅有限大小的图像 f(x,y) 做傅里叶变换时,数学上默认是将其在空域进行了无限周期延拓(即不断重复这幅图像)。这就是为什么傅里叶变换的结果具有周期性——因为输入被默认为是周期的。
3. 直观理解:“无限重复的频谱”
想象你计算了一幅图像的傅里叶变换,得到了频谱 F(u,v)。如果你沿着u轴或v轴平移 N 的整数倍,你会看到完全相同的频谱图案在不断重复。

4. 案例演示
下列案例只是为了演示傅里叶变换的周期性,实际应用中,我们只需要计算一个周期内的结果(大小为M x N)就足够了,因为其他周期都是重复的。
# 计算 FFT 并中心化
fft2 = np.fft.fft2(img_gray) #对图像进行傅里叶变换
fft_shift = np.fft.fftshift(fft2) # 将原点移到中心
magnitude_centered_log = 20 * np.log(np.abs(fft_shift) + 1) # 取对数,增强可视性
# 截取频谱的一个象限,并复制拼接,模拟周期延拓
# 为了简化,我们取左上角 1/4 区域 (M//2 x N//2)
quadrant = magnitude_centered_log[:M//2, :N//2]
# 拼接成 2x2 的周期图案
periodic_demo = np.vstack([
np.hstack([quadrant, quadrant]),
np.hstack([quadrant, quadrant])
])
show_images(
[magnitude_centered_log, periodic_demo],
['中心化频谱 (一个周期)', '频谱的周期延拓模拟 (重复4次)']
)
print("\n观察:右图中四个象限的图案完全相同,模拟了频谱的周期性。")
print("结论:DFT 结果在频域以 (M, N) 为周期无限重复。")
print("应用:实际计算只需要一个周期的频谱。")
观察 :右图中四个象限的图案完全相同,模拟了频谱的周期性。
结论 :DFT 结果在频域以 (M, N) 为周期无限重复。
应用 :实际计算只需要一个周期的频谱。
5. 应用场景
DFT的计算范围:实际计算DFT时,我们只需要计算一个周期内的结果(大小为M x N)就足够了,因为其他周期都是重复的。
4. 平移性
平移性
1. 空域平移 → 频域相位变化
空域中图像的平移,不会改变其频域的幅度谱(即 “有什么频率成分”不变 ),只会改变其相位谱(即“频率成分的位置信息”改变)。

DFT的原点,即F(0,0)被设置在u=N/2和v=N/2,即将f(x,y)的傅立叶变换的原点移动到相应频率方阵的中心。即称之为频谱中心化。

图(b)为原始信号的频谱图,图(c)为将频谱原点搬移到中心之后的频谱图。由图可知,频谱中心化后,低频成份集中在中心,而高频成份位于四周,这样有助于我们观察频谱。
2. 案例演示
# 1. 空域平移对频域的影响
rows, cols = img_gray.shape
tx, ty = 50, 50 # 平移量 (向右50,向下50)
# 创建平移矩阵并应用
M_trans = np.float32([[1, 0, tx], [0, 1, ty]])
img_shift = cv2.warpAffine(img_gray, M_trans, (cols, rows), borderMode=cv2.BORDER_CONSTANT)
# 计算原图和平移图的 FFT 幅度谱
fft_original = np.fft.fft2(img_gray)
fft_shifted = np.fft.fft2(img_shift)
mag_original = np.abs(np.fft.fftshift(fft_original))
mag_shifted = np.abs(np.fft.fftshift(fft_shifted))
# 2. 频谱中心化 (频域平移)
fft_original = np.fft.fft2(img_gray)
fft_centered = np.fft.fft2(img_gray * ((-1)**np.arange(rows)[:, None] * (-1)**np.arange(cols))) # 空域乘以 (-1)^(x+y)
show_images(
[img_gray, img_shift, 20*np.log(mag_original+1), 20*np.log(mag_shifted+1)],
['原图', f'平移 ({tx},{ty}) 后的图像', '原图频谱幅度', '平移后图像频谱幅度']
)
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.imshow(20*np.log(np.abs(np.fft.fftshift(fft_original)) + 1), cmap='gray')
plt.title('未中心化的频谱 (低频在角落)')
plt.axis('off')
plt.subplot(122)
plt.imshow(20*np.log(np.abs(np.fft.fftshift(fft_centered)) + 1), cmap='gray')
plt.title('中心化后的频谱 (低频在中心)')
plt.axis('off')
plt.tight_layout()
plt.show()
print("\n结论1:空域平移后,频谱幅度谱不变,相位谱改变。")
print("结论2:空域乘以 (-1)^(x+y) 可将频谱低频分量移到中心,方便观察。")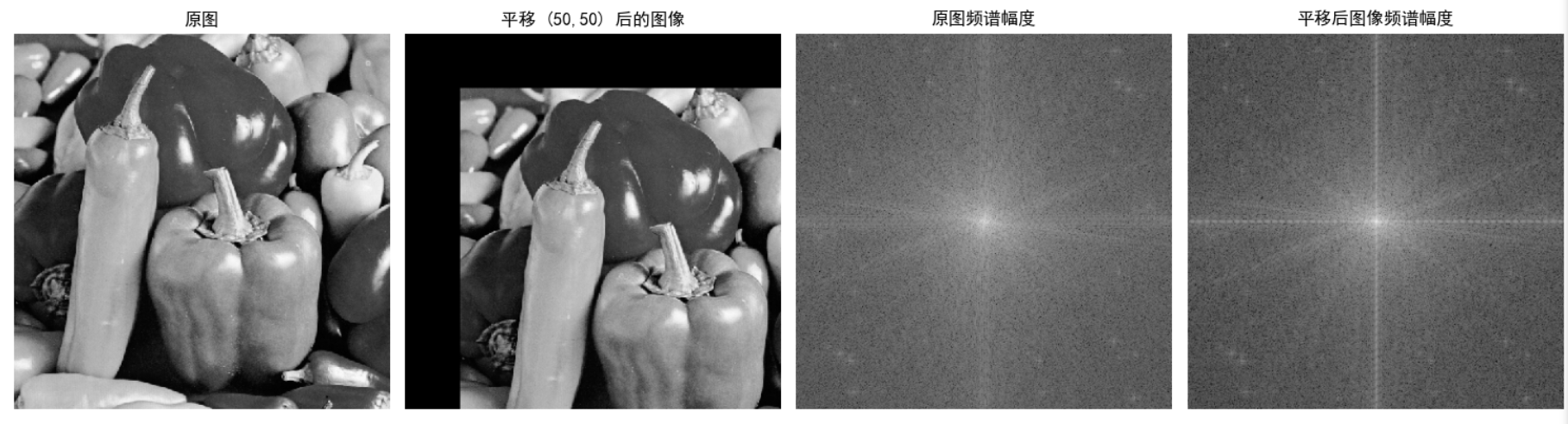

结论1 :空域平移后,频谱幅度谱不变,相位谱改变。
结论2 :空域乘以 (-1)^(x+y) 可将频谱低频分量移到中心,方便观察。
3. 应用场景
频谱中心化 :方便观察和分析频域特性。
5.旋转不变性
旋转不变性
1. 什么是旋转不变性?
空域中图像的旋转,会导致其频域的频谱 也发生相同角度的旋转。其幅度谱的形状保持不变,只是方向变了。

2. 案例演示
import numpy as np
import cv2
from matplotlib import pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负
#平移
def move(img,dx=10,dy=10):
rows,cols= img.shape[:2]
M0 = np.float32([[1,0,dx],[0,1,dy]])
dst0 = cv2.warpAffine(img,M0,(cols,rows))
return dst0
def rotate(img,angle=45):
rows,cols=img.shape[:2]
M1=cv2.getRotationMatrix2D((cols/2,rows/2),angle ,1)
# 第三个参数是输出图像的尺寸
dst1=cv2.warpAffine(img,M1,(cols,rows),flags=cv2.INTER_LANCZOS4)
return dst1
#旋转不变性和平移性
box = np.zeros((128, 128), np.uint8)
print(type(box))
shape = box.shape
for i in range(shape[0]):
for j in range(shape[1]):
if j in range(60, 68) and i in range(32,96):
box[i,j] = 255
img0=box
img1=rotate(box,45)
img2=move(box,20,20)
dft0 = np.fft.fft2(img0)
dft_shift0=np.fft.fftshift(dft0)
magnitude0= 20*np.log(1+np.abs(dft_shift0))#幅值谱
dft1 = np.fft.fft2(img1)
dft_shift1=np.fft.fftshift(dft1)
magnitude1= 20*np.log(1+np.abs(dft_shift1))#幅值谱
dft2 = np.fft.fft2(img2)
dft_shift2=np.fft.fftshift(dft2)
magnitude2= 20*np.log(1+np.abs(dft_shift2))#幅值谱
plt.figure(figsize=(10,6))
plt.subplot(231),plt.imshow(img0, cmap = 'gray')
plt.title('原图像'), plt.axis('off')
plt.subplot(232),plt.imshow(img1, cmap = 'gray')
plt.title('旋转45度的图像'), plt.axis('off')
plt.subplot(233),plt.imshow(img2, cmap = 'gray')
plt.title('平移后图像'), plt.axis('off')
plt.subplot(234),plt.imshow(magnitude0, cmap = 'gray')
plt.title('原图像幅值谱'), plt.axis('off')
plt.subplot(235),plt.imshow(magnitude1, cmap = 'gray')
plt.title('旋转图像幅值谱'), plt.axis('off')
plt.subplot(236),plt.imshow(magnitude2, cmap = 'gray')
plt.title('平移图像幅值谱'), plt.axis('off')
plt.savefig("ch4-12.jpg")
plt.show()
观察:频谱的主要特征(如亮条纹方向)随图像旋转了相同角度。
结论:空域旋转导致频域同角度旋转,体现了旋转不变性。
应用:可用于分析图像中的方向性纹理。
3. 应用场景
图像匹配与识别 :如果两个图像具有旋转不变性的特征(如基于傅里叶变换幅度谱的特征),那么即使它们发生了旋转,也能被识别出来。
理解频域能量分布 :图像中某个方向的纹理越丰富,频谱上对应方向的能量(亮点)就越强。
6. 卷积定理 —— 最重要的性质!
前言
1. 空域卷积 = 频域乘积
这是傅里叶变换最核心、最有用的性质!
卷积定理 告诉我们: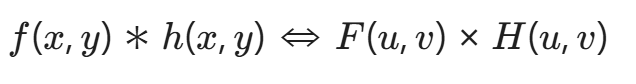
左边:空域中,图像 f(x,y) 与卷积核 h(x,y)(如平滑核、锐化核)进行卷积操作。
右边:频域中,图像的傅里叶变换 F(u,v) 与卷积核的傅里叶变换H(u,v)(称为传递函数)进行相乘操作。
反过来也成立(频域卷积 = 空域乘积,这里我们重点关注上面那个)。
2. 为什么这个性质如此重要?
因为空域卷积计算量很大 ,而频域乘积计算量小得多 (尤其结合FFT算法)!
步骤:
- 对 f(x,y) 和 h(x,y) 分别做 FFT 得到 F(u,v) 和 H(u,v)。
- 在频域将 F(u,v)×H(u,v)。
- 对结果做 IFFT 变换回空域,得到卷积结果。
3. 案例演示
# 定义空域高斯卷积核
def gaussian_kernel(size, sigma):
x = np.linspace(-(size//2), size//2, size) # 生成 x 轴坐标
g = np.exp(-0.5 * (x**2) / (sigma**2)) # 高斯函数
g = g / g.sum() # 归一化
kernel = np.outer(g, g) # 外积得到二维高斯核
return kernel
kernel_size = 15 # 高斯核大小
sigma = 3 # 高斯核标准差
kernel = gaussian_kernel(kernel_size, sigma) # 生成高斯核
# 1. 空域卷积
# 方法1: 空域卷积 (使用 cv2.filter2D)
conv_spatial = cv2.filter2D(img_gray, -1, kernel, borderType=cv2.BORDER_CONSTANT) #BORDER_CONSTANT 表示边界填充为常数0
# 方法2: 频域乘积 (利用卷积定理)
# 1. 补零,避免循环卷积效应 (conv2 函数默认补零)
pad_h = img_gray.shape[0] + kernel_size - 1
pad_w = img_gray.shape[1] + kernel_size - 1
# 2. FFT
fft_img = np.fft.fft2(img_gray, s=(pad_h, pad_w))
fft_kernel = np.fft.fft2(kernel, s=(pad_h, pad_w)) # 核也补零到相同大小
# 3. 频域乘积
fft_conv = fft_img * fft_kernel
# 4. IFFT 并取实部 (去除可能的微小虚部)
conv_freq = np.fft.ifft2(fft_conv).real
# 裁剪回原图大小 (去除补零部分)
conv_freq = conv_freq[:img_gray.shape[0], :img_gray.shape[1]]
# 显示结果
show_images(
[img_gray, conv_spatial, conv_freq],
['原图', '空域卷积结果 (高斯平滑)', '频域乘积结果 (高斯平滑)']
)
print("\n结论:两种方法得到的平滑结果几乎完全一致,验证了卷积定理。")
print("应用:频域滤波的理论基础,尤其适合大卷积核的场景。")
结论 :两种方法得到的平滑结果几乎完全一致,验证了卷积定理。
应用 :频域滤波的理论基础,尤其适合大卷积核的场景。
4 ·应用场景
- 所有线性滤波操作:平滑、锐化、边缘检测等。例如:
- 低通滤波(平滑):频域乘以一个低通传递函数(保留低频,抑制高频)。
- 高通滤波(锐化):频域乘以一个高通传递函数(保留高频,抑制低频)。
- 快速卷积计算:是信号处理和图像处理中快速算法的基础。
总结
| 性质 | 核心思想 | 典型应用场景 |
|---|---|---|
| 可分离性 | 2D FFT = 1D FFT (行) + 1D FFT (列) | FFT算法实现的基础,加速计算 |
| 共轭对称性 | 实信号频谱幅度对称 | 频谱可视化、数据压缩 |
| 周期性 | 频谱无限重复 | 理解DFT的计算范围,避免频谱混叠概念 |
| 平移性 | 空域平移 → 频域相位变;频谱中心化 | 频谱显示、相位分析 |
| 旋转不变性 | 空域旋转 → 频域同角度旋转 | 方向性纹理分析、旋转图像匹配 |
| 卷积定理 | 空域卷积 ↔ 频域乘积 (最重要) | 所有线性滤波(平滑、锐化、边缘检测),大幅提升效率 |
