第三章 空域图像增强_空域锐化
锐化滤波
1 锐化滤波的基本原理
锐化滤波的基本原理
1.我们为什么要锐化?
大家还记得我们之前学过的平滑滤波(比如均值滤波、高斯滤波)吗?它的主要目的是什么?
是去除噪声,让图像变得更平滑。但平滑有一个副作用,就是会让图像的边缘、轮廓等细节变得模糊。
锐化滤波的目的恰恰相反:它不是为了平滑,而是为了突出和增强图像中的细节、边缘和轮廓,让图像看起来更清晰、更“锐利”。

平滑:像在照片上蒙上一层薄纱,让过渡更柔和。
锐化:像是用一支更细的笔去描边,让边界更分明。
锐化的本质是什么?
在数学上,图像的边缘和细节部分,其实就是灰度发生剧烈变化的地方 。而描述变化快慢 的工具,正是我们微积分里学过的——微分。所以,图像锐化的基础就是空域微分 。
2.空域微分的基本思想
想象一下一幅从左到右亮度逐渐增加的图像,它的灰度变化曲线是平缓的斜坡。而在一个物体的边缘处,灰度会有一个突然的跳变,曲线会变得很陡峭。
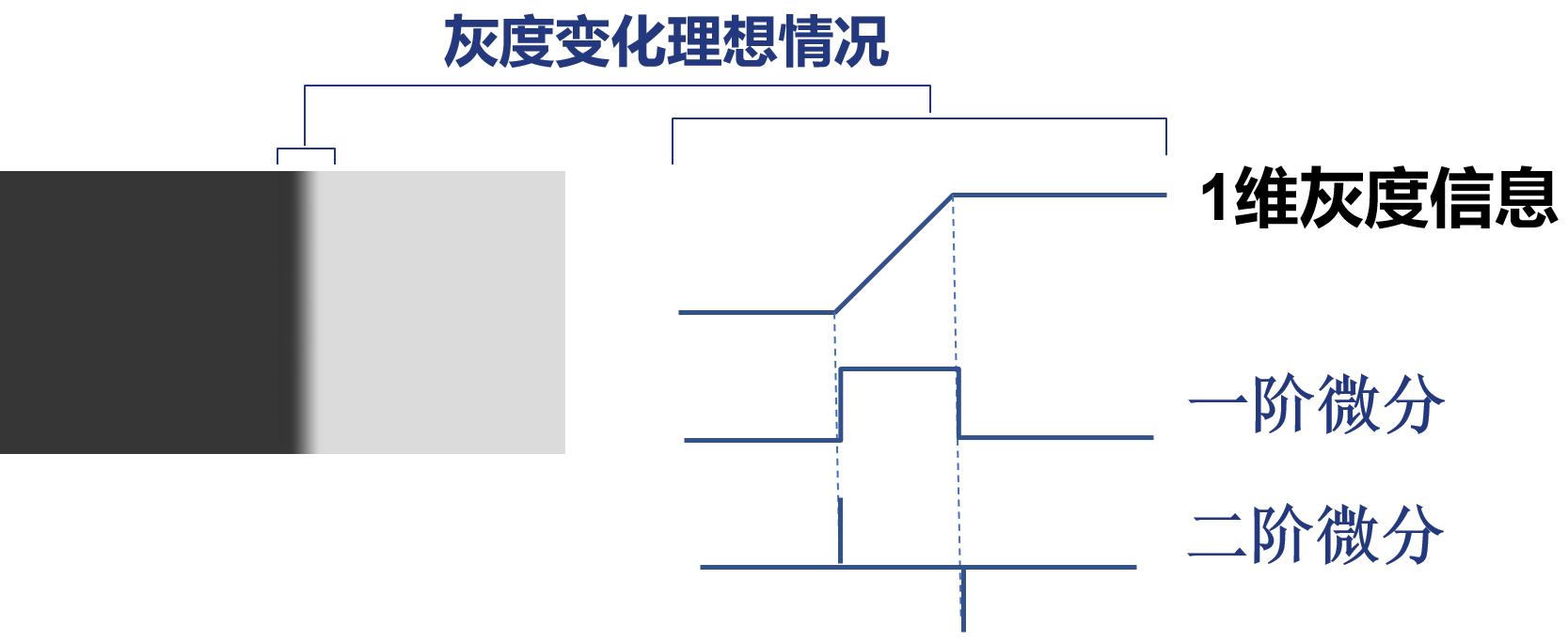
一阶微分:衡量的是变化的速度。在平缓区域,一阶微分值接近0;在陡峭的边缘,一阶微分值会很大。所以,一阶微分会产生一个很宽的“边缘”。
二阶微分:衡量的是变化速度的变化率,也就是曲线的斜率变化。在平缓区域,二阶微分值为0; 在灰度跳变的边缘起点(从平缓变陡峭),二阶微分会产生一个正脉冲 ;在边缘的终点(从陡峭变平缓),会产生一个负脉冲 。这意味着,二阶微分会产生一个双边缘,并且能够突出灰度变化的方向。
核心结论:通过计算图像每个像素点的微分值,我们可以找到灰度变化剧烈的区域(即边缘),然后通过某种方式将这些信息叠加回原图,就能达到增强边缘、锐化图像的目的。👈 👍 👍 👍
在离散的数字图像中,我们用“差分”来近似“微分”。常见的一阶微分算子通过卷积模板来实现。
3.核心概念
1. 梯度 (Gradient)
在二维图像中,我们需要同时考虑水平和垂直两个方向的变化。
对于一个图像函数 f(x,y),其在点 (x, y) 的梯度是一个矢量,定义为:
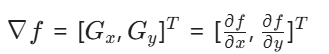
G x:水平梯度(X方向导数)
描述的是水平方向(从左到右) 的灰度变化。
它对垂直边缘最敏感(因为垂直边缘左右两侧的灰度差异最大)。
Gy:垂直梯度(Y方向导数)
描述的是垂直方向(从上到下) 的灰度变化。
它对水平边缘最敏感。
这个矢量的两个重要属性是: 👇
梯度幅度 (Gradient Magnitude):表示边缘的强度。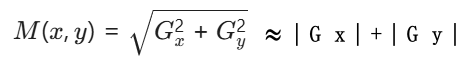
梯度方向 (Gradient Direction):表示边缘的朝向。边缘方向总是与梯度方向垂直。
2. 卷积模板
在数字图像中,我们用差分来近似微分。通过卷积模板可以轻松计算Gx和Gy。
1. Roberts 算子(元老,但已较少使用)
- 模板大小:2x2
- 模板:
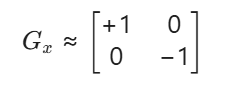
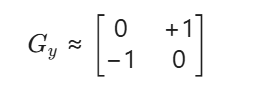
特点:计算最快,但对噪声非常敏感(因为模板小,没有平滑能力)。
平滑就是“抹平”或“模糊”,目的是为了让图像的整体色调过渡更柔和,去掉那些刺眼的、不和谐的“毛刺”(也就是噪声)
在数字图像中,“不平滑”就是指相邻像素之间的灰度值差异很大。
2. 普里维特 Prewitt 算子(引入了平滑思想)
模板大小:3x3
模板:
- 左边的Gx(检测垂直边缘),设计逻辑:先对左列(-1)和右列(+1)分别求和(相当于平滑),再求差。中间列权重为0。
- 右边Gy(检测水平边缘)
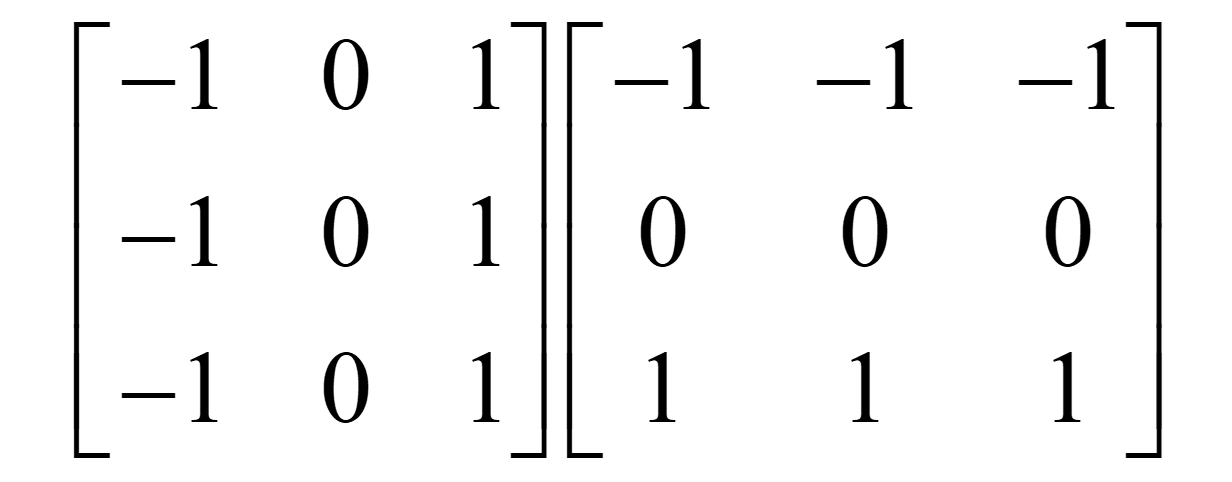
特点:由于引入了平滑,抗噪声能力比Roberts强。
3. 索贝尔 Sobel 算子(Prewitt算子的改进版,最常用、效果最佳)
- 模板大小:3x3
- 模板
- 左边的Gx(检测垂直边缘)
- 右边Gy(检测水平边缘)
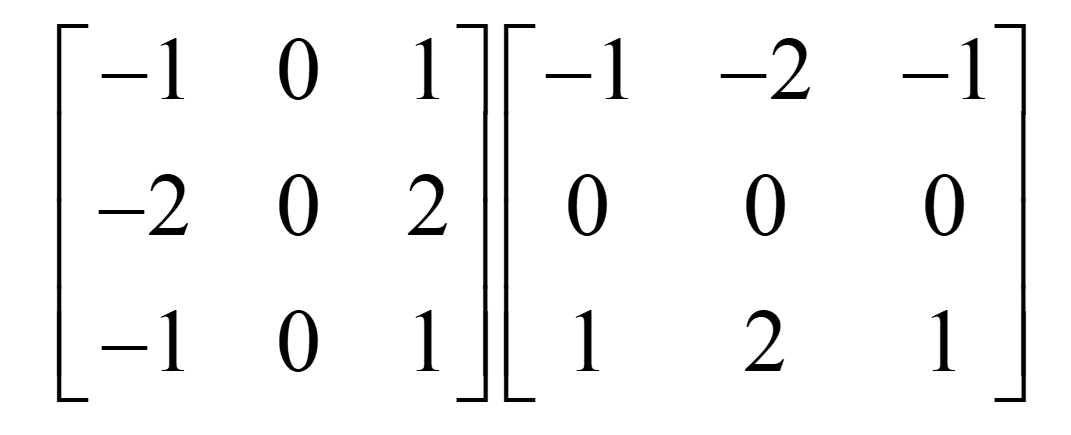
- 核心改进:在Prewitt的基础上,将中心行(对于Gx)和中心列(对于Gy)的权重翻倍(变为2),使其对边缘的响应比普里维特算子更明显,因此效果通常更好。
- 为什么更好? 这相当于强调了对当前像素最直接的邻居的影响,从而在平滑噪声和精确定位边缘之间取得了更好的平衡。Sobel检测到的边缘通常比Prewitt的更清晰、更连续。
4. 简单案例说明(一阶微分)
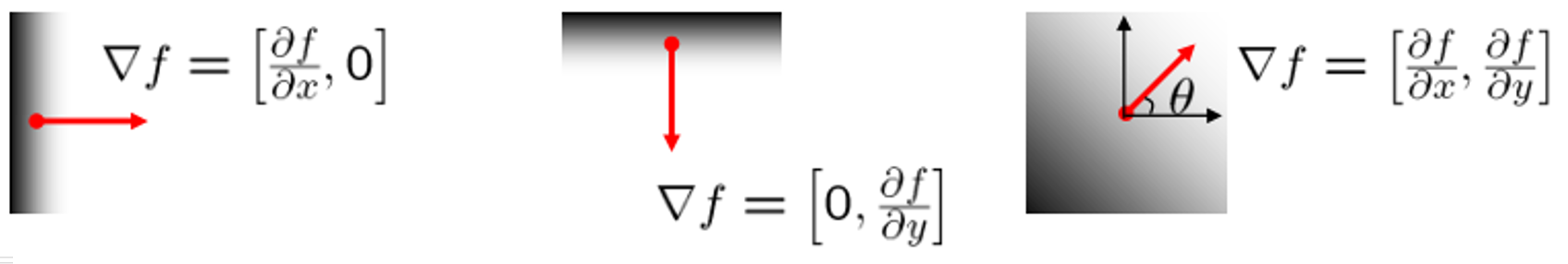
让我们用一个极度简化的3x3图像区域来计算Sobel梯度。类似上图 ☝️
假设我们有一个区域,左边暗,右边亮,形成一个垂直边缘。
[ 10, 10, 100 ]
[ 10, 10, 100 ]
[ 10, 10, 100 ]第1步:计算水平梯度Gx(使用Sobel的Gx模板)
将模板中心对准灰度值为10的中间像素:
图像区域 Gx模板
[ 10, 10, 100 ] [ -1, 0, +1 ]
[ 10, (10), 100 ] * [ -2, 0, +2 ] =
[ 10, 10, 100 ] [ -1, 0, +1 ]
计算:
= (10*-1) + (10*0) + (100*1) +
(10*-2) + (10*0) + (100*2) +
(10*-1) + (10*0) + (100*1)
= (-10 + 0 + 100) + (-20 + 0 + 200) + (-10 + 0 + 100)
= (90) + (180) + (90)
= 360解读:我们得到了一个很大的正数Gx=360, 这说明在水平方向上,存在一个从左(暗)到右(亮)的剧烈变化,即一个垂直边缘。
第2步:计算垂直梯度Gy(使用Sobel的Gy模板)
同样的区域和中心像素:
图像区域 Gy模板
[ 10, 10, 100 ] [ -1, -2, -1 ]
[ 10, (10), 100 ] * [ 0, 0, 0 ] =
[ 10, 10, 100 ] [ +1, +2, +1 ]
计算:
= (10*-1) + (10*-2) + (100*-1) +
(10*0) + (10*0) + (100*0) +
(10*1) + (10*2) + (100*1)
= (-10 -20 -100) + (0 + 0 + 0) + (10 + 20 + 100)
= (-130) + (0) + (130)
= 0解读:Gy=0,这意味着在垂直方向上,上下灰度完全一致,没有变化。这符合我们的预期,因为这是一个完美的垂直边缘。 👈 😄
第3步:计算梯度幅度 M
M = sqrt(Gx^2 + Gy^2) = sqrt(360^2 + 0^2) = 360
这个值很大,明确指示此处有一个强烈的边缘。
第4步:计算梯度方向 θ
θ=arctan(Gy/Gx) = arctan(0/360) = 0°
梯度方向是0°(水平向右)。而边缘的方向与梯度方向垂直,所以这个边缘是垂直方向(90°) 的,完全正确! 👈 😄 😄
2.二阶微分算子
前言
一阶微分看的是速度,而二阶微分看的是加速度,即变化率的变化率。

1. 拉普拉斯算子(Laplacian)
拉普拉斯算子是最常用的各向同性二阶微分算子。
1. 数学定义
对于二维图像函数 (x,y),其拉普拉斯算子定义为两个方向二阶导数的和:
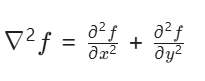
2. 离散卷积模板(关键!)
拉普拉斯蜕化算子:(中心为负)
[ 0, 1, 0 ]
[ 1, -4, 1 ]
[ 0, 1, 0 ]
拉普拉斯增强算子:(中心为正)
[ 0, -1, 0]
[ -1, 5, -1 ]
[ 0, -1, 0 ]2. 详细数字案例
我们假设有一个平坦区域,中心有一个稍亮的点。
[ 10, 10, 10 ]
[ 10, 40, 10 ] <-- 中心像素(值为40)比周围(值为10)亮,形成一个“边缘”
[ 10, 10, 10 ]步骤1:计算中心像素的拉普拉斯值
1️⃣ 使用蜕化算子:
图像区域 锐化算子
[ 10, 10, 10 ] [ 0, 1, 0 ]
[ 10, (40), 10 ] * [ 1, -4, 1 ] =
[ 10, 10, 10 ] [ 0, 1, 0 ]
计算:
= (10*0) + (10*1) + (10*0) +
(10*1) + (40*-4) + (10*1) +
(10*0) + (10*1) + (10*0)
= (0) + (10) + (0) +
(10) + (-160) + (10) +
(0) + (10) + (0)
= -120解读:拉普拉斯值为-120,这意味着此处有一个强烈的边缘。
步骤2:解读结果
我们得到了一个很大的负值(-120)。这完全符合拉普拉斯算子的理论:
对于暗区域中的亮点(相当于边缘的亮侧),拉普拉斯会产生一个负脉冲。
这个值(-120)量化了中心点与其周围环境的差异程度。差异越大,这个值的绝对值就越大。
步骤3:手动锐化(使用锐化公式)
锐化公式:g = f + c * (∇²f),这里我们取 c = -1(因为我们的蜕化算子中心是负的,要用负系数来校正)。
对于中心像素:
g_center = f_center + (-1) * (∇²f) = 40 + (-1) * (-120) = 40 + 120 = 160
手动锐化后的中心像素值变成了160!
2️⃣ 使用“增强算子”一步到位
将算子中心对准图像的40这个像素:
原图像区域 增强算子
[ 10, 10, 10 ] [ 0, -1, 0 ]
[ 10, (40), 10 ] * [ -1, 5, -1 ] =
[ 10, 10, 10 ] [ 0, -1, 0 ]
计算:
= (10*0) + (10*-1) + (10*0) +
(10*-1) + (40*5) + (10*-1) +
(10*0) + (10*-1) + (10*0)
= (0) + (-10) + (0) +
(-10) + (200) + (-10) +
(0) + (-10) + (0)
= 160我们直接得到了和手动计算一模一样的结果:160。
边缘增强: 中心像素(40)原本只比周围(10)高30个灰度级。经过锐化后,它变成了160,比周围高了150个灰度级!
对比度提升: 边缘两侧的对比度被极大地增强了。这个点现在在画面中显得异常突出。
视觉清晰度: 整幅图像中,所有类似这种灰度突变的地方(边缘、轮廓、细节)都会得到同样的增强,因此图像看起来就更清晰、更锐利。
结论: 👇
拉普拉斯蜕化算子 帮助我们理解锐化的原理:先提取细节(二阶微分),再叠加回原图。
拉普拉斯增强算子 是我们在实际图像处理中直接使用的工具,它高效且方便。
案例:👇
import matplotlib.pyplot as plt
import cv2
import numpy as np
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负
img=cv2.imread(r"./img/moon.jpg",0)
#拉普拉斯锐化:
fi1=np.array([[0,1,0],[1,-4,1],[0,1,0]]) #拉普拉斯蜕化算子
fi2=np.array([[0,-1,0],[-1,5,-1],[0,-1,0]]) #拉普拉斯增强算子
#使用opencv的卷积函数 滤波去噪声
img1 = cv2.filter2D(img,-1,fi1,borderType=cv2.BORDER_DEFAULT) #拉普拉斯锐化,-1 表示输出类型和输入相同,fi1是卷积核,borderType=cv2.BORDER_DEFAULT表示默认的边界处理方式
img2 = cv2.filter2D(img,-1,fi2,borderType=cv2.BORDER_DEFAULT) #拉普拉斯增强,-1 表示输出类型和输入相同,fi2是卷积核,borderType=cv2.BORDER_DEFAULT表示默认的边界处理方式
# 这个公式在教材的61页
# 拉普拉斯算子常用来改善因为光线的漫反射造成的图像模糊,所用的方法是用原图像减去拉普拉斯滤波图像。
img3=img-img1
#输出对应的图片
plt.figure(figsize=(12,6))
plt.subplot(141)
plt.imshow(img,vmin=0,vmax=255,cmap=plt.cm.gray)#设置内部的坐标,以及灰度的最大值和最小值
plt.title("原图像")
plt.axis('off')
plt.subplot(142)
plt.imshow(img1,vmin=0,vmax=255,cmap=plt.cm.gray)
plt.title("拉普拉斯滤波图像")
plt.axis('off')
plt.subplot(143)
plt.imshow(img2,vmin=0,vmax=255,cmap=plt.cm.gray)
plt.title("拉普拉斯锐化增强图像")
plt.axis('off')
plt.subplot(144)
plt.imshow(img3,vmin=0,vmax=255,cmap=plt.cm.gray)
plt.title("原图像减去拉普拉斯滤波图像")
plt.axis('off')
plt.savefig("ch3-43.jpg")
plt.show()
3.平滑滤波与锐化滤波的核心区别
平滑滤波与锐化滤波的核心区别
| 平滑滤波 (Smoothing/Blurring) | 锐化滤波 (Sharpening) |
|---|---|
| 目的:削弱或消除图像中的高频分量(如噪声、细节、边缘),保留低频分量(平缓区域)。 | 目的:增强图像中的高频分量(如细节、边缘),使图像更清晰。 |
| 效果:图像变得模糊、柔和。 | 效果:图像边缘更清晰、细节更突出。 |
| 数学本质:通常基于积分或平均的思想。 | 数学本质:通常基于微分或差分的思想。 |
判断一个滤波核是平滑还是锐化,主要看它对图像高频分量(边缘/细节)的作用!
滤波核A (3x3):
[-2, 1, -2]
[ 1, 5, 1]
[-2, 1, -2]
滤波核B (3x3,带系数1/6):
1/6 * [
[-1, -1, -1],
[ 2, 2, 2],
[ 1, 1, 1]
]
滤波核C (3x3):
[ 1, 1, 0]
[ 1, 0, -1]
[ 0, -1, -1]
滤波核D (3x3,带系数1/20):
1/20 * [
[1, 2, 1],
[2, 3, 2],
[1, 2, 1]
]| 特征 | 平滑滤波核 | 锐化滤波核 |
|---|---|---|
| 元素符号 | 几乎全为正(或有少量小的负数,但整体是平均) | 必有负数,且中心为较大的正数(或中心为负、周围为正的拉普拉斯蜕化核) |
| 归一化系数 | 常有(如1/9, 1/16, 1/20),确保输出亮度正常 | 可无(或隐含系数,如拉普拉斯增强核中心为5,周围为-1) |
| 权重和 | 通常为1(或被归一化系数处理后为1) | 通常为0或较小的正数/负数(强调差异) |
| 对边缘的作用 | 削弱边缘(模糊) | 增强边缘(清晰) |
口诀:
全正(或主要为正)求平均 → 平滑!
中心正大、周围有负 → 锐化!
正负交错、差分形式 → 锐化(边缘检测)!
最终答案 👇
滤波核A:锐化滤波
滤波核B:平滑滤波
滤波核C:锐化滤波(边缘检测类)
滤波核D:平滑滤波
4.梯度的各向同性
梯度的各向同性
在图像处理中,梯度表示像素值的变化率和方向。
前面已经讲过
4.1 各向同性
- 在各个方向上表现一致
- 旋转不变性:无论图像如何旋转,滤波效果相同
- 例如:拉普拉斯算子(对所有方向的边缘敏感)
- 应用场景:
医学图像分析
特点:细胞、肿瘤等通常没有固定方向
原因:需要公平检测所有方向的边界天文图像处理
特点:星星、星系、环形山是圆形的
原因:旋转不变性很重要材质纹理分析
特点:木材、石材等自然纹理方向随机
原因:不知道边缘的具体方向特征点检测
特点:寻找角点、斑点等特征
原因:需要全方位响应
案例代码: 👇
import matplotlib.pyplot as plt
import numpy as np
import cv2
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 各向同性在医学图像中的应用示例
def medical_image_example():
# 模拟细胞图像(圆形物体)
cell_image = np.zeros((200, 200))
# 创建几个模拟细胞
cv2.circle(cell_image, (50, 50), 20, 1, -1) # 细胞1
cv2.circle(cell_image, (120, 80), 25, 1, -1) # 细胞2
cv2.circle(cell_image, (80, 150), 15, 1, -1) # 细胞3
# 添加噪声模拟真实情况
cell_image += np.random.normal(0, 0.1, cell_image.shape)
# 应用各向同性算子(拉普拉斯)
laplacian = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]]) # 拉普拉斯锐化
# [0, 1, 0]
# [1, -4, 1]
# [0, 1, 0]
# laplacian = np.array([[0, -1, 0], [-1, 5, -1], [0, -1, 0]]) # 拉普拉斯增强
# [ 0, -1, 0]
# [ -1, 5, -1 ]
# [ 0, -1, 0 ]
edges_isotropic = cv2.filter2D(cell_image, -1, laplacian) # 各向同性
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.imshow(cell_image, cmap='gray')
plt.title('模拟细胞图像\n(圆形物体)')
plt.axis('off')
plt.subplot(1, 3, 2)
plt.imshow(np.abs(edges_isotropic), cmap='hot')
plt.title('各向同性边缘检测\n(所有细胞边界都清晰)')
plt.axis('off')
plt.subplot(1, 3, 3)
# 显示各向同性的旋转不变性
rotated = np.rot90(cell_image)
edges_rotated = cv2.filter2D(rotated, -1, laplacian)
plt.imshow(np.abs(edges_rotated), cmap='hot')
plt.title('旋转后检测结果\n(效果不变)')
plt.axis('off')
plt.tight_layout()
plt.show()
print("各向同性在医学图像中的优势:")
print("✓ 细胞是圆形的,需要全方位检测")
print("✓ 不知道细胞的具体朝向")
print("✓ 旋转图像后,分析结果应该一致")
medical_image_example()
4.2 各向异性 (Anisotropic)
- 在不同方向上表现不同
- 对方向敏感,某些方向的响应更强
- 例如:Sobel算子(对水平/垂直边缘敏感)
- 应用场景:
建筑物检测
特点:建筑物主要是水平和垂直边缘
原因:只需要检测特定方向文档图像处理
特点:文字、表格主要是水平垂直方向
原因:方向明确,效率高道路检测
特点:道路通常有明确的方向性
原因:针对特定方向优化工业质检
特点:检测特定方向的划痕、缺陷
原因:只关心特定方向的异常
案例代码: 👇
# 各向异性在文档处理中的应用
def document_processing_example():
# 模拟文档图像(主要是水平垂直边缘)
document = np.zeros((200, 200))
# 添加文字行(水平线)
for i in range(30, 180, 25):
document[i:i+3, 20:180] = 1
# 添加表格线
document[50:53, 20:180] = 1 # 水平表格线
document[100:103, 20:180] = 1 # 水平表格线
document[20:150, 80:83] = 1 # 垂直表格线
document[20:150, 140:143] = 1 # 垂直表格线
# 应用各向异性算子(Sobel)
sobel_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]]) # 检测垂直边缘
# [-1, 0, 1]
# [-2, 0, 2]
# [-1, 0, 1]
sobel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]]) # 检测水平边缘
# [-1, -2, -1]
# [ 0, 0, 0]
# [ 1, 2, 1]
vertical_edges = cv2.filter2D(document, -1, sobel_x)
horizontal_edges = cv2.filter2D(document, -1, sobel_y)
plt.figure(figsize=(15, 5))
plt.subplot(1, 4, 1)
plt.imshow(document, cmap='gray')
plt.title('模拟文档图像\n(文字和表格)')
sobel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]]) # 检测水平边缘
vertical_edges = cv2.filter2D(document, -1, sobel_x) # 检测垂直边缘
horizontal_edges = cv2.filter2D(document, -1, sobel_y) # 检测水平边缘
plt.figure(figsize=(15, 5))
plt.subplot(1, 4, 1)
plt.imshow(document, cmap='gray')
plt.title('模拟文档图像\n(文字和表格)')
plt.axis('off')
plt.subplot(1, 4, 2)
plt.imshow(np.abs(vertical_edges), cmap='hot')
plt.title('Sobel X - 垂直边缘\n(检测到表格竖线)')
plt.axis('off')
plt.subplot(1, 4, 3)
plt.imshow(np.abs(horizontal_edges), cmap='hot')
plt.title('Sobel Y - 水平边缘\n(检测到文字行和表格横线)')
plt.axis('off')
plt.subplot(1, 4, 4)
# 组合结果
combined = np.abs(vertical_edges) + np.abs(horizontal_edges)
plt.imshow(combined, cmap='hot')
plt.title('组合结果\n(完整的文档结构)')
plt.axis('off')
plt.tight_layout()
plt.show()
print("各向异性在文档处理中的优势:")
print("✓ 文档主要是水平垂直结构")
print("✓ 可以分别处理不同方向")
print("✓ 计算效率高,适合实时处理")
document_processing_example()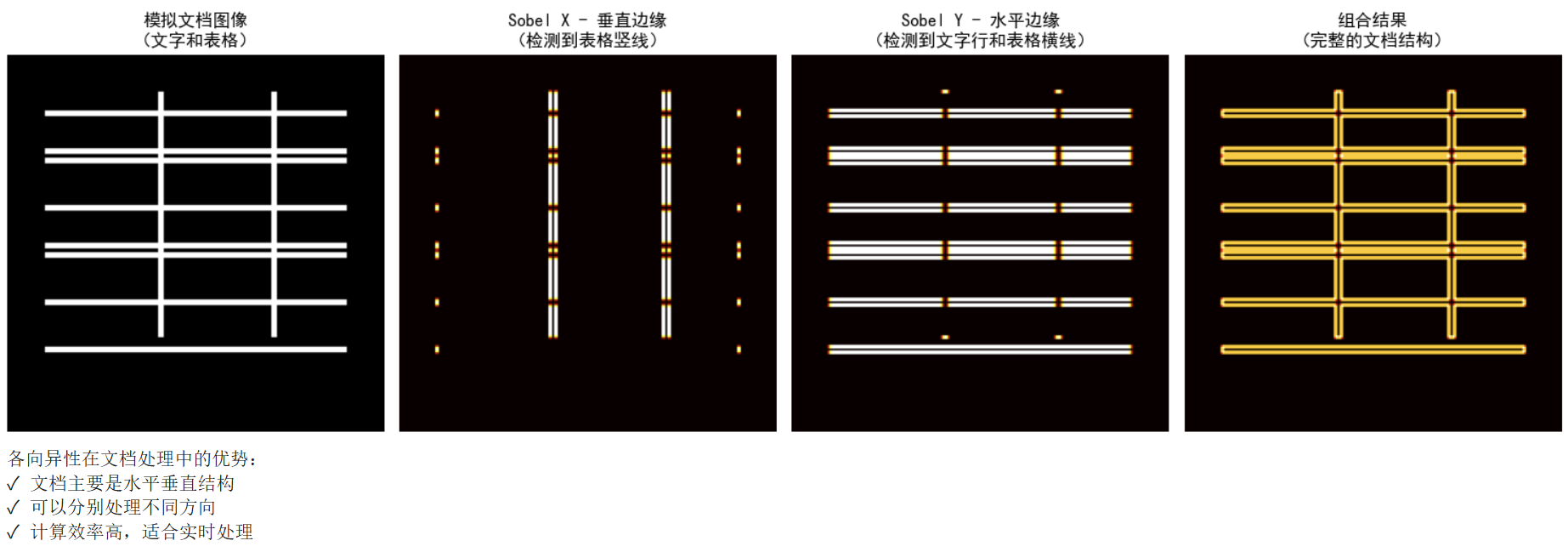
5. 拓展,USM锐化
前言
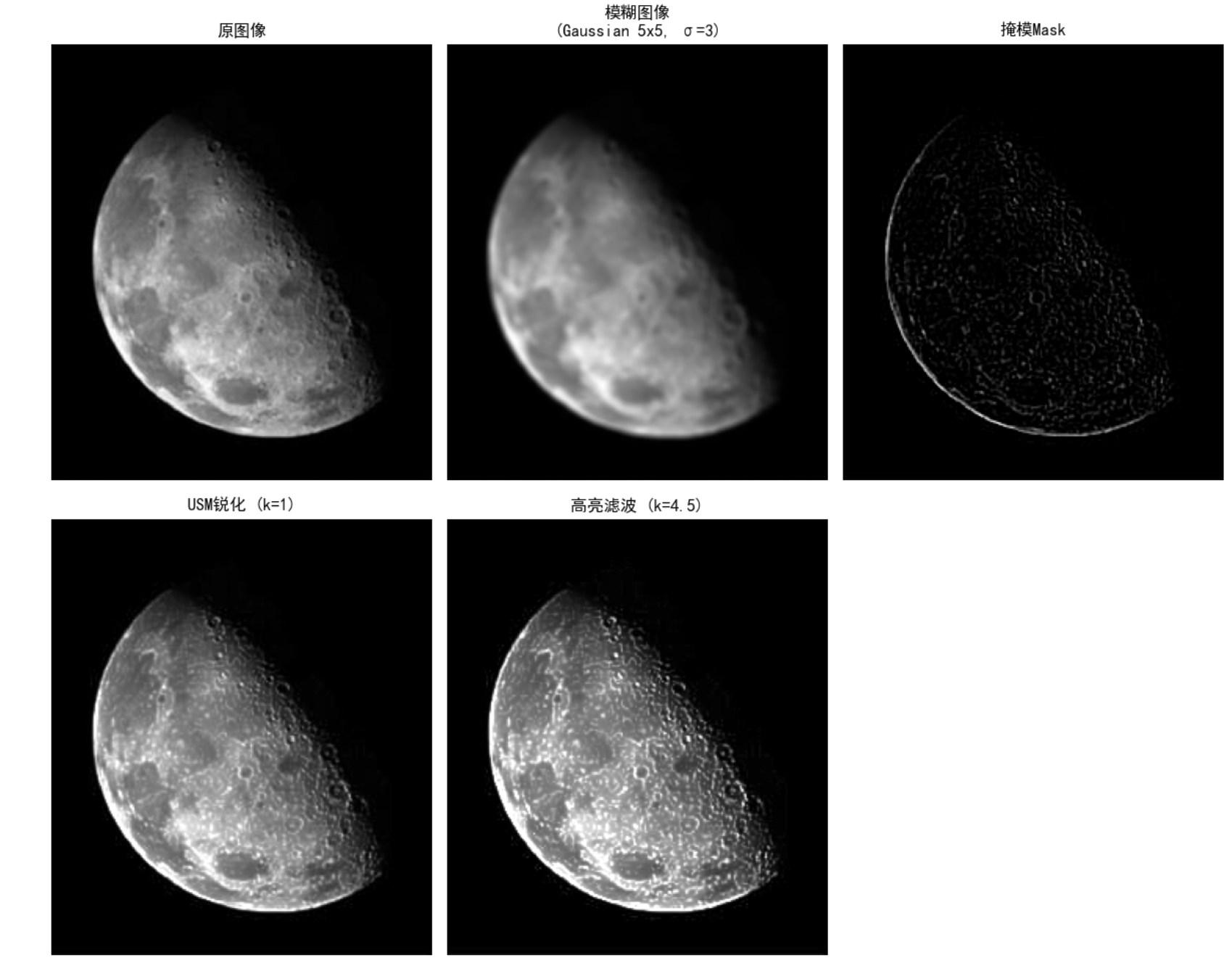
USM锐化是一种经典的图像锐化技术,基本原理是:通过原图像与模糊图像的差异来提取边缘细节,然后将细节增强后叠加回原图像。
数学公式:锐化图像 = 原图像 + 权重 × (原图像 - 模糊图像)
应用场景
- 摄影后期处理:增强照片细节和清晰度
- 医学影像:突出病变边缘,辅助诊断
- 文档扫描:改善文字可读性
- 卫星图像:提升地物识别能力
案例代码: 👇
import matplotlib.pyplot as plt
import cv2
import numpy as np
%matplotlib inline
# 确保中文正常显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取图像
img = cv2.imread(r"./img/moon.jpg", 0) # 以灰度图读取
# 图像效果处理函数
def process_image(image):
# 1. 模糊图像 (Gaussian 5x5, σ=3)
blurred = cv2.GaussianBlur(image, (5, 5), sigmaX=3)
# 2. 掩模Mask (原图 - 模糊图像)
# 掩模作用:提取原图像与模糊图像的差异,即边缘细节
mask = cv2.subtract(image, blurred)
# 3. USM锐化 (k=1):原图 + k×掩模
usm_k1 = cv2.addWeighted(image, 1, mask, 1, 0) # 权重1,掩模1,偏移量0
usm_k1 = np.clip(usm_k1, 0, 255).astype(np.uint8) # 防止溢出
# 4. 高亮滤波 (k=4.5):原图 + k×掩模
highlight_k45 = cv2.addWeighted(image, 1, mask, 4.5, 0)
highlight_k45 = np.clip(highlight_k45, 0, 255).astype(np.uint8) # 防止溢出
return blurred, mask, usm_k1, highlight_k45
# 处理图像
blurred_img, mask_img, usm_img, highlight_img = process_image(img)
# 显示所有效果
plt.figure(figsize=(12, 10))
# 1. 原图像
plt.subplot(2, 3, 1) # 3行2列,第1个
plt.imshow(img, cmap='gray')
plt.title("原图像")
plt.axis('off')
# 2. 模糊图像 (Gaussian 5x5, σ=3)
plt.subplot(2, 3, 2)
plt.imshow(blurred_img, cmap='gray')
plt.title("模糊图像\n(Gaussian 5x5, σ=3)")
plt.axis('off')
# 3. 掩模Mask
plt.subplot(2, 3, 3)
plt.imshow(mask_img, cmap='gray')
plt.title("掩模Mask")
plt.axis('off')
# 4. USM锐化 (k=1)
plt.subplot(2, 3, 4)
plt.imshow(usm_img, cmap='gray')
plt.title("USM锐化 (k=1)")
plt.axis('off')
# 5. 高亮滤波 (k=4.5)
plt.subplot(2, 3, 5)
plt.imshow(highlight_img, cmap='gray')
plt.title("高亮滤波 (k=4.5)")
plt.axis('off')
plt.tight_layout()
plt.savefig("image_enhancement_results.jpg", dpi=300, bbox_inches='tight')
plt.show()