数据仓库与数据挖掘-第一章节
1. 直方图均衡化
前言
1. 什么是直方图均衡化
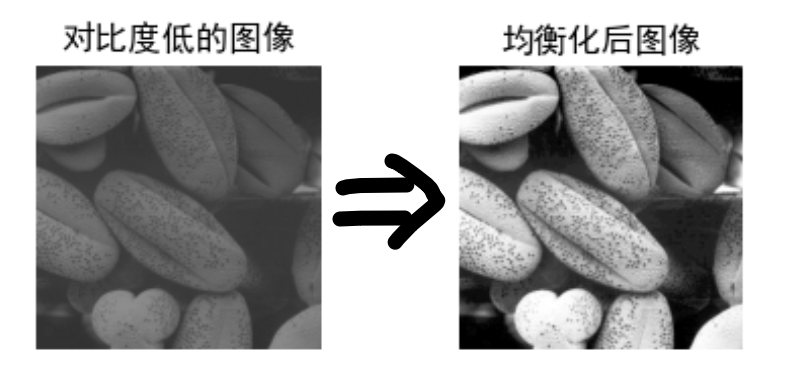
直方图均衡化是一种通过重新分配图像像素的灰度值,使图像的灰度直方图尽可能均匀分布,从而增强图像对比度的图像处理技术。
简单来说,它能把一张“灰蒙蒙”、对比度不强的图像,变成一张黑白分明、细节更清晰的图像。
2.为什么需要它?
很多图像由于光照不足、曝光过度或成像设备动态范围有限,其灰度值会集中在一个狭窄的区间内。这导致图像看起来对比度很低,细节难以分辨。例如:
- 背光拍摄的人像:人脸部分太暗,看不清细节。
- 雾天拍摄的风景:整个画面发白,景物模糊。
- 医学X光片:某些组织之间的对比度差异很小,难以诊断。
直方图均衡化就是为了解决这些问题而设计的。
3. 核心思想与工作原理
它的核心目标是将原始图像的灰度分布(直方图)拉伸得更均匀,覆盖整个可能的灰度范围(通常是0-255)
工作原理可以分为以下几个步骤:
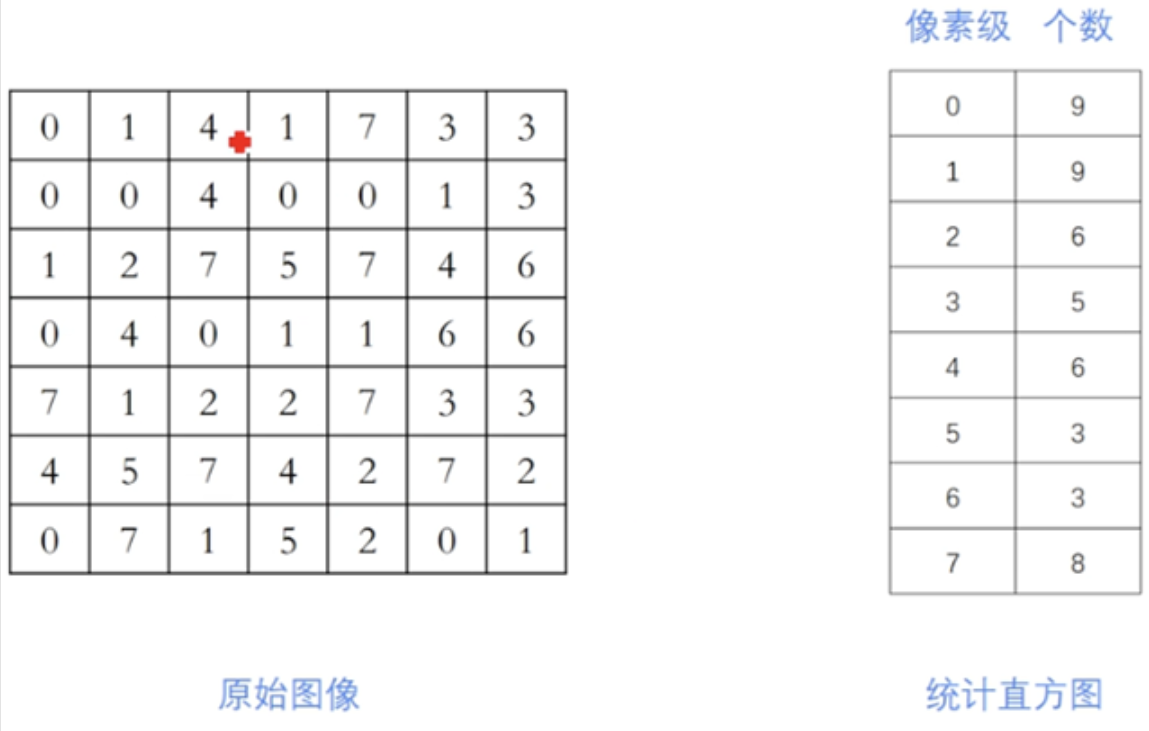
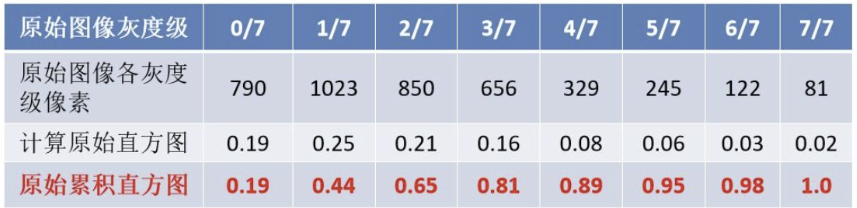
1. 计算原始直方图:
统计图像中每一个灰度级(如0到255)出现的像素个数。
2. 计算累计分布函数(CDF):
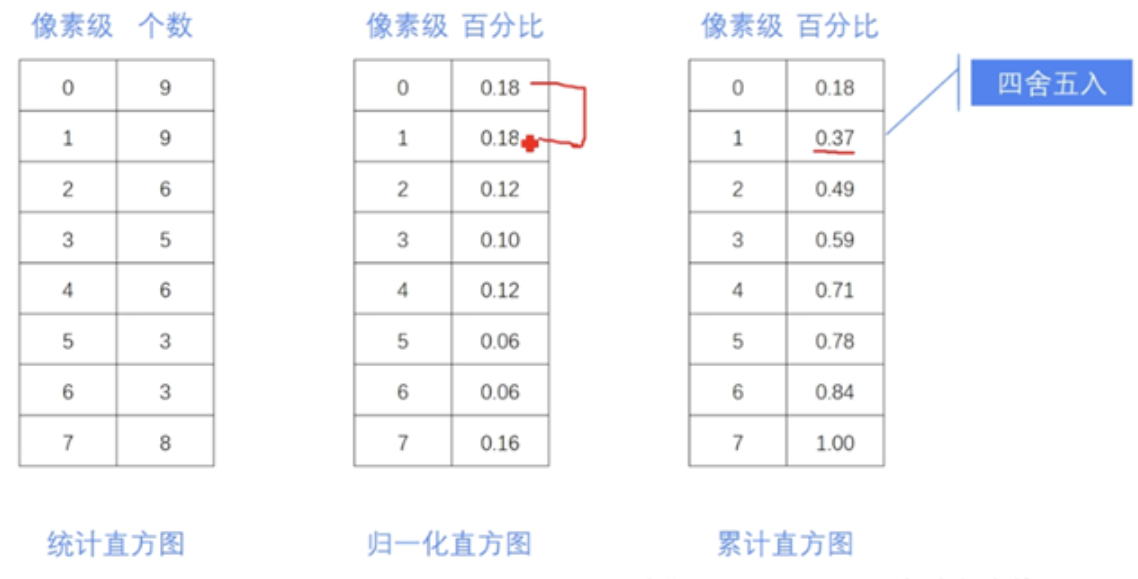
计算每个灰度级的累积概率。公式为:
CDF(i) = Sum(Histogram(0) to Histogram(i)) / TotalPixels其中,Histogram(i) 是第i个灰度级的像素个数,TotalPixels 是图像中所有像素的总数。
这意味着 CDF(255) 应该等于 1(或255,取决于归一化方式)。
3.映射到新的灰度值:

这是最关键的一步。利用计算出的CDF,将每个原始灰度值 i 映射到一个新的灰度值 j。
映射公式为:j = CDF(i) * (MaxGrayLevel - 1)
- MaxGrayLevel 是最大灰度值(例如,8位图像就是255)。
- CDF(i) 是第i个灰度级的累积概率。
这个公式的作用是,将原本分布不均匀的累积概率,线性地拉伸到整个灰度范围。
4.生成新图像:
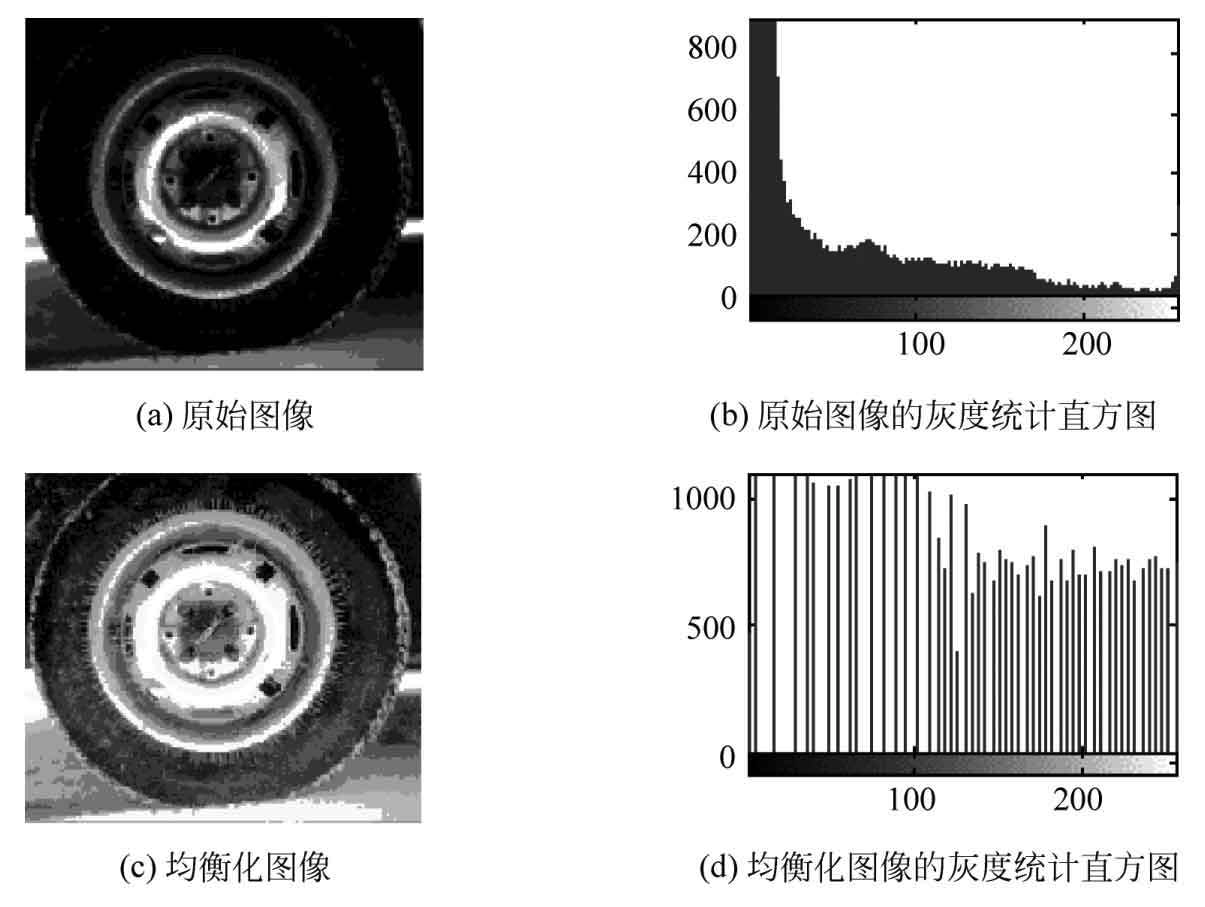
由上图的结果可知,原先8个灰度级转变成6个灰度级,那么原始直方图和均衡直方图为:

由上图可以看出,虽然二者相似,但右侧均衡化后的直方图分布更均匀,相邻像素级概率和与高概率近似相等。如果将两张图的灰度级放在同一区间,可以看出差别更大。
4.直方图均衡的缺点
综上所述,直方图均衡化的优点是能够增强整个图像的对比度。其缺点主要包括:
- 增强效果不易控制,处理的结果总是得到全局均匀化的直方图。
- 均衡化图像的动态范围扩大,本质上是扩大了量化间隔,但量化级别(灰度级)反而减少了,导致某些图像细节消失。
- 对于直方图存在高峰的图像,经处理后对比度可能过分增强。
- 导致出现伪轮廓;原来灰度值不同的像素经过处理后可能变为相同,从而形成一片灰度值相同的区域,各区域之间有明显的边界,导致出现伪轮廓。
5. 直方图均衡化案例
import numpy as np
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负
#图像直方图
def histogram(image):
(row, col) = image.shape
#创建长度为256的list
hist = [0]*256
for i in range(row):
for j in range(col):
hist[image[i,j]] += 1
hist=hist/np.sum(hist) #这里一定要用np.sum,python的列表不是直接除以一个整数
return hist
def global_linear_transmation(im,c=0,d=255): #c,d是线性变换的参数
img=im.copy()
maxV = img.max()
minV = img.min()
if maxV==minV:
return np.uint8(img)
for i in range(img.shape[0]):
for j in range(img.shape[1]):
img[i, j] = ((d-c) / (maxV - minV)) * (img[i, j] - minV)+c#img[i,j]代表的是某像素点三通道的值
return np.uint8(img)
if __name__=="__main__":
img = cv2.imread(r'./img/rice.tif',0)
img1=global_linear_transmation(img,0,100) #偏暗
img2=global_linear_transmation(img,100,255) #偏亮
img3=global_linear_transmation(img,50,150) #对比度低
img4 = cv2.equalizeHist(img) #均衡化
#计算直方图
h1=histogram(img1)
h2=histogram(img2)
h3=histogram(img3)
h4=histogram(img4)
plt.figure(figsize=(10,4))
plt.subplots_adjust(left=None, bottom=None, right=None, \
top=None,wspace=0.4, hspace=0.2)
plt.subplot(241)
plt.title("偏暗图像")
plt.axis("off")
plt.imshow(img1,vmin=0, vmax=255,cmap =plt.cm.gray)
plt.subplot(242)
plt.title("偏亮图像")
plt.axis("off")
plt.imshow(img2,vmin=0, vmax=255,cmap =plt.cm.gray)
plt.subplot(243)
plt.title("对比度低的图像")
plt.axis("off")
plt.imshow(img3,vmin=0, vmax=255,cmap =plt.cm.gray)
plt.subplot(244)
plt.title("均衡化后图像")
plt.axis("off")
plt.imshow(img4,vmin=0, vmax=255,cmap =plt.cm.gray)
plt.subplot(245)
# plt.title("偏暗直方图")
plt.bar(range(256),h1)
plt.xlabel("灰度值")
plt.ylabel("概率")
# plt.ylim(0,0.05)
plt.subplot(246)
# plt.title("偏亮直方图")
plt.bar(range(256),h2)
plt.xlabel("灰度值")
plt.ylabel("概率")
# plt.ylim(0,0.05)
plt.subplot(247)
# plt.title("对比度低图像直方图")
plt.bar(range(256),h3)
plt.xlabel("灰度值")
plt.ylabel("概率")
# plt.ylim(0,0.05)
plt.subplot(248)
# plt.title("均衡化后直方图")
plt.bar(range(256),h4)
plt.xlabel("灰度值")
plt.ylabel("概率")
# plt.ylim(0,0.05)
plt.show()
plt.savefig("ch03-20_equ.jpg")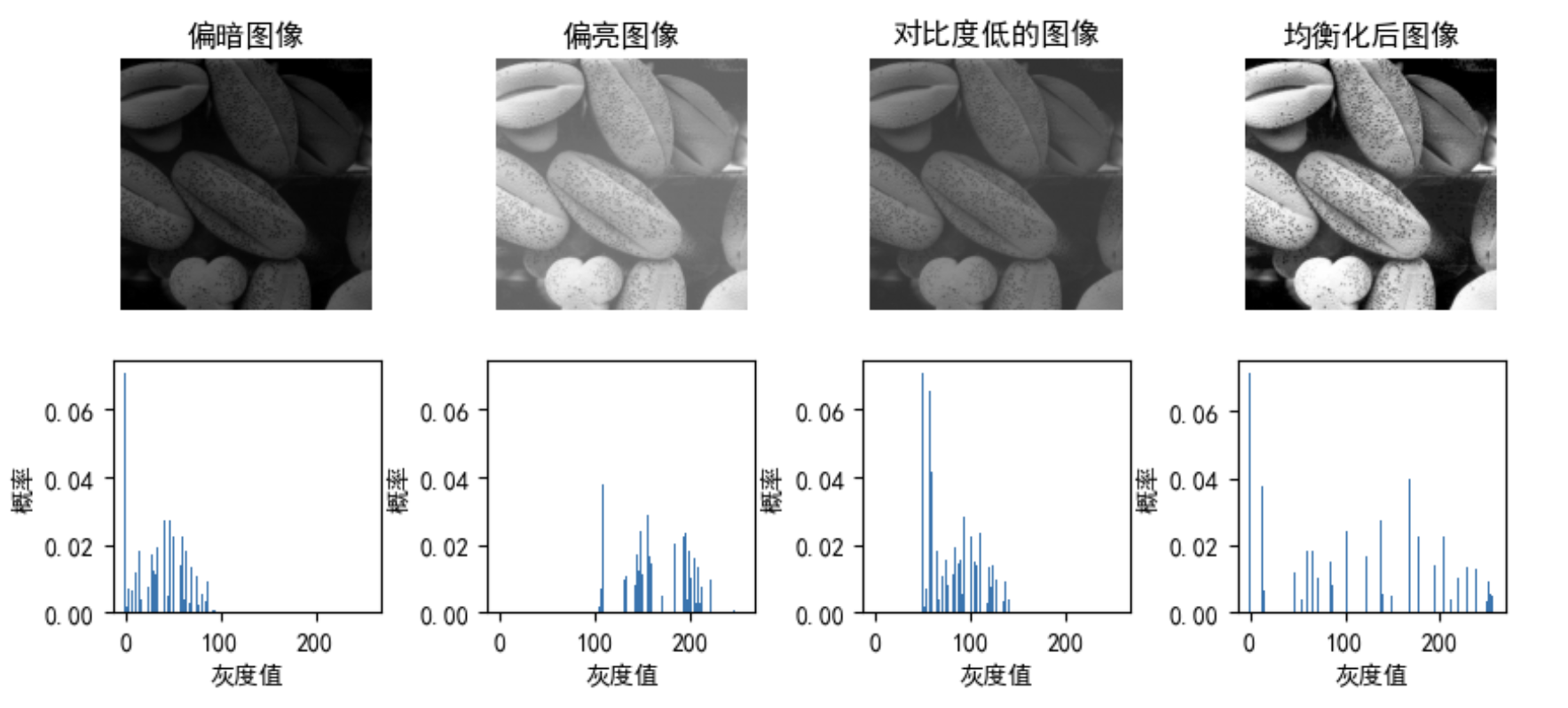
2. 直方图规定化
前言
1.什么是直方图规定化?
- 定义: 直方图规定化是指一幅输入图像经过点运算变化,将原图像的灰度直方图改造成所希望的直方图形状。
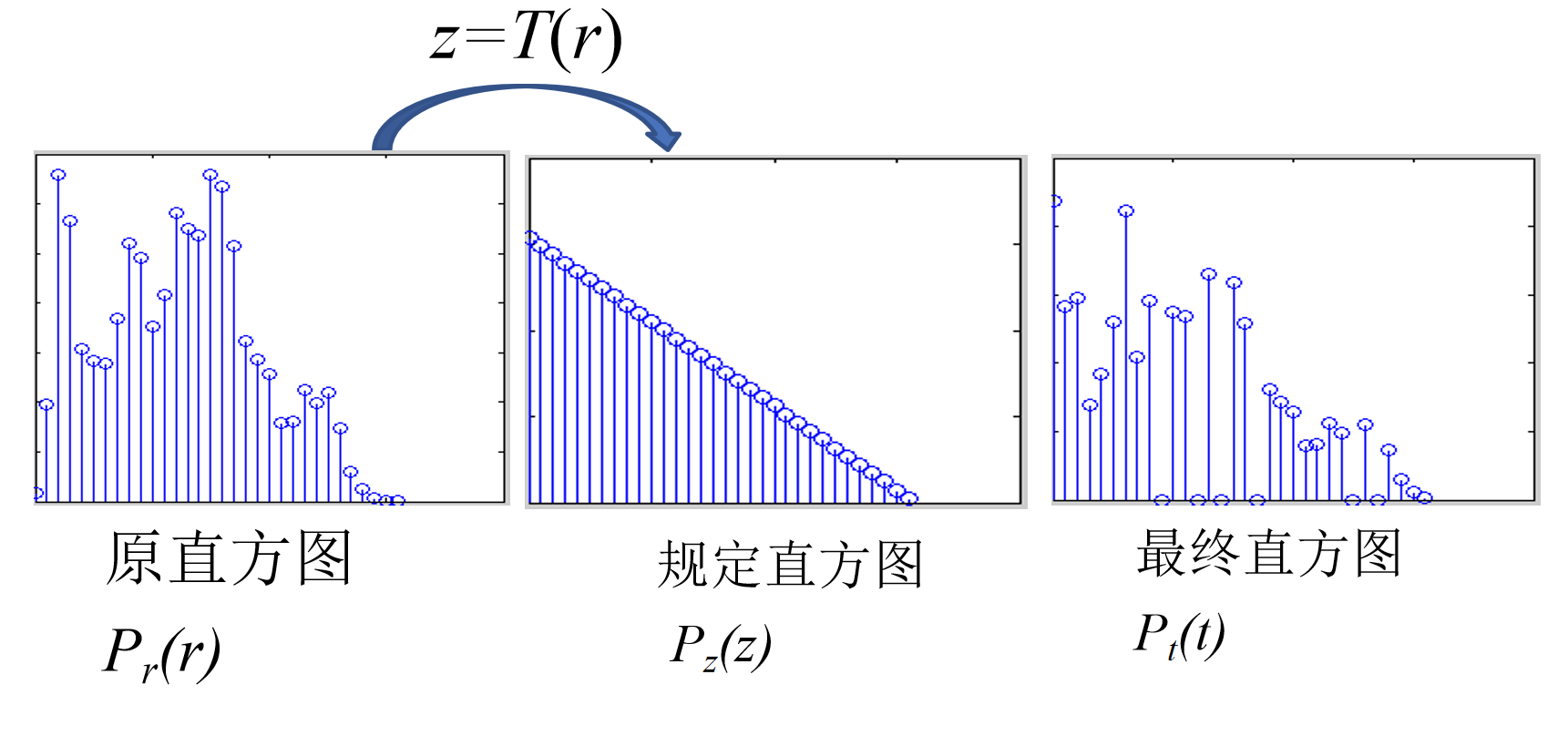
给定原直方图pr (r) 和规定直方图pz (z) ,目标是求解一个变换z=T(r),使得图像的直方图趋向规定直方图
- 目的:变换直方图使之成为某个想要的形状。但由于数字图像的灰度级是离散并且是有限的,所以直方图规定化的结果一般只是与目标直方图的形状大体接近,并非理想的完全一致。
- 功效:比直方图均衡化更加灵活(直方图均衡化可看成特殊的直方图规定化),常用与图片风格一致性的自动处理。
- 实际应用场景
- 医学影像处理:将不同设备拍摄的图像标准化到相同的对比度范围
- 遥感图像处理:使不同时间拍摄的卫星图像具有可比性
- 图像风格迁移:将一幅图像的色调特征应用到另一幅图像
- 图像增强:根据特定需求调整图像对比度
2.直方图规定化有两种方式:SML单映射和GML组映射
1️⃣ SML单映射的实现原理是:
- 首先 计算原始图像和规定目标的累计直方图(将统计直方图归一化到(0, 1)之间,再计算累计概率分布函数)
- 然后对原图像的累计直方图寻求一一映射关系(每个灰度值映射到与目标的累计直方图最近的点)。

- 有了映射关系后,遍历原图像的每个像素点,做相应的点运算变换即可。

SML中,我们是依次遍历原图累加直方图,在规定累加直方图寻找最靠近自己的。在GML(组映射)中,就变成了依次从规定累加直方图中,对比原图累加直方图,也是找到最靠近的值,进行灰度变换,只是这里的变换规则变了。
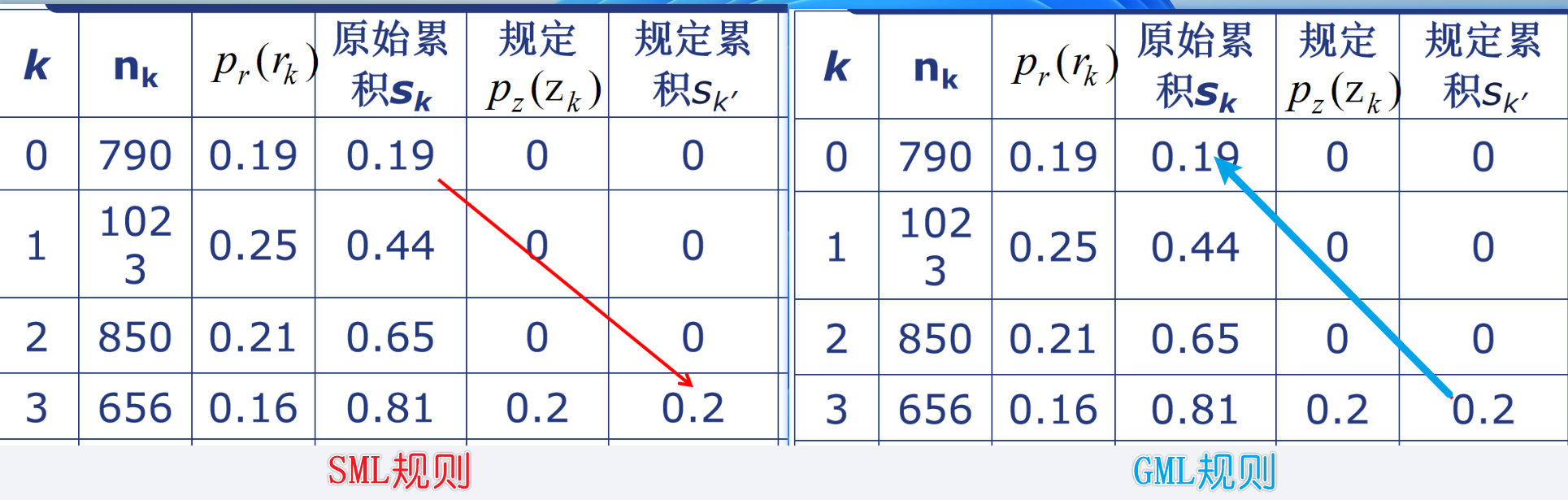
2️⃣GML单映射的实现原理是:
首先计算原始图像和规定目标的累计直方图(将统计直方图归一化到(0, 1)之间,再计算累计概率分布函数),
然后对原图像的累计直方图进行分组:先在原图像的累计直方图中找到与目标直方图的每个灰度值距离最近的点(如下图的所示的 0→3;3→5;7→7,即0,3,7为在原图像中要找的点),让点与点之间构成一组,映射到目标直方图中对应的灰度值。
有了映射关系后,遍历原图像的每个像素点,做相应的点运算变换即可。
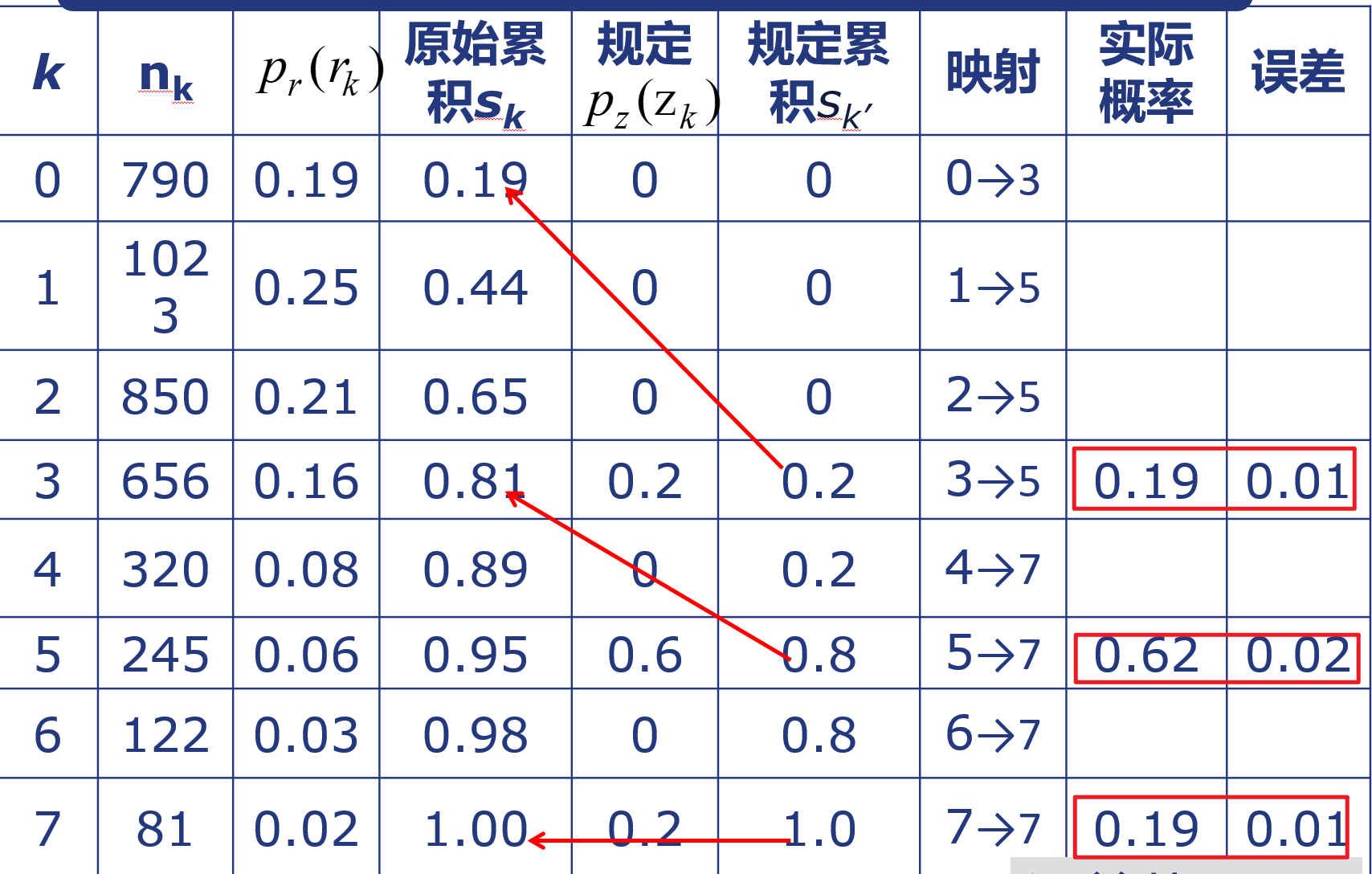
3.案例👇
1.准备方法
import numpy as np
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format="retina"
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 图像直方图
def histogram(image):
(row, col) = image.shape
# 创建长度为256的list
hist = [0] * 256
for i in range(row):
for j in range(col):
hist[image[i, j]] += 1
hist = hist / np.sum(hist) # 这里一定要用np.sum,python的列表不是直接除以一个整数
return hist
# 规定化直方图
# type=1目标直方图是正三角形,type=2倒三角形,type=3平形,
def regulation_histogram(img, type=1, mapSML=True):
'''
:param img::输入图像
:param type: type=1目标直方图是正三角形,type=2倒三角形,type=3平形,
:param mapSML: True是SML False是GML
:return: 直方图和图像
'''
rows, cols = img.shape
gray_flat = img.reshape((rows * cols,))
# 修复:将 np.float 改为 float
dif = np.zeros((256, 256), float) # 用于存放原直方图与目标直方图的差
S = np.zeros((rows, cols), np.uint8) # 单映射规定化后图像
G = np.zeros((rows, cols), np.uint8) # 组映射规定化后图像
src = np.zeros((256,), np.int32) # 原直方图
dst = np.zeros((256,), np.int32) # 规定直方图
H_SML = np.zeros((256,), np.int32) # 单映射的映射关系
H_GML = np.zeros((256,), np.int32) # 组映射的映射关系
SH = np.zeros((256,), float) # 单映射规定化后直方图
GH = np.zeros((256,), float) # 组映射规定化后直方图
# 计算原图像各个灰度级数量
for index, value in enumerate(gray_flat):
src[value] += 1
# 归一化处理
src_pro = src / sum(src)
# 计算灰度级的累计分布
for i in range(1, 256):
src_pro[i] = src_pro[i - 1] + src_pro[i]
# 目标直方图为正直角三角形
if type == 1:
for i in range(256):
dst[i] = i
# 目标直方图为倒三角形
if type == 2:
for i in range(256):
dst[i] = 256 - i
# 目标直方图是平行的
if type == 3:
for i in range(256):
dst[i] = 128
# 归一化处理
dst_pro = dst / sum(dst)
# 计算规定化灰度级的累计分布
for i in range(1, 256):
dst_pro[i] = dst_pro[i - 1] + dst_pro[i]
# |V2-V1|计算目标直方图与原直方图的差
for i in range(256):
for j in range(256):
dif[i, j] = abs(src_pro[i] - dst_pro[j])
# SML单映射
if mapSML == True:
for i in range(256):
minx = 0
minvalue = dif[i, 0]
for j in range(1, 256):
if (dif[i, j] < minvalue):
minvalue = dif[i, j]
minx = j
H_SML[i] = minx # 将灰度i映射为灰度minx
for i in range(256):
SH[H_SML[i]] += src[i] # src[i]是灰度为i的像素个数,SH是规定化后的直方图
SHpro = SH / sum(SH)
for i in range(rows):
for j in range(cols):
S[i, j] = H_SML[img[i, j]] # S是单映射得到的图像,将灰度值img[i,j]映射为H_SML[img[i,j]]
return SHpro, S
else:
# GML群映射
lastStartY = 0
lastEndY = 0
startY = 0
endY = 0
for i in range(256):
minvalue = dif[0, i]
for j in range(1, 256):
if (minvalue > dif[j, i]):
minvalue = dif[j, i]
endY = j
if (startY != lastStartY) or (endY != lastEndY):
for k in range(startY, endY + 1):
H_GML[k] = i
lastStartY = startY
lastEndY = endY
startY = lastEndY + 1
for i in range(256):
GH[H_GML[i]] += src[i] # 组映射直方图
for i in range(rows):
for j in range(cols):
G[i, j] = H_GML[img[i, j]] # G是组映射得到的图像
GHpro = GH / sum(GH) # 归一化直方图
return GHpro, G
# 全局线性变换
def global_linear_transmation(im, c=0, d=255):
img = im.copy()
maxV = img.max()
minV = img.min()
if maxV == minV:
return np.uint8(img)
for i in range(img.shape[0]):
for j in range(img.shape[1]):
img[i, j] = ((d - c) / (maxV - minV)) * (img[i, j] - minV) + c # img[i,j]代表的是某像素点三通道的值
return np.uint8(img)2.运行主程序
# 主程序
img1 = cv2.imread(r'./img/rice.tif', 0)
# img1=global_linear_transmation(img0,c=50,d=200)
plt.figure(figsize=(12, 6))# 设置图像大小
plt.subplots_adjust(left=None, bottom=None, right=None, \
top=None, wspace=0.4, hspace=0.3) # 调整子图间距
plt.subplot(241)
hist1 = histogram(img1)
plt.bar(range(256), hist1)
plt.ylim(0, 0.02)
plt.xlabel("灰度值")
plt.ylabel("各灰度值出现概率")
plt.title("原直方图")
dst = np.zeros((256,), np.int32) # 规定直方图
for j in range(256):
dst[j] = j
dst = dst / np.sum(dst)
plt.subplot(242)
plt.bar(range(256), dst)
plt.ylim(0, 0.02)
plt.xlabel("灰度值")
plt.ylabel("各灰度值出现概率")
plt.title("规定直方图")
# 现在重新运行修复后的函数
histr1, equ1 = regulation_histogram(img1.copy(), 1, True) # 这里的True是SML,False是GML
plt.subplot(243)
plt.bar(range(256), histr1)
plt.ylim(0, 0.02)
plt.xlabel("灰度值")
plt.ylabel("各灰度值出现概率")
plt.title("SML规定化直方图")
histr2, equ2 = regulation_histogram(img1.copy(), 1, False)# 这里的True是SML,False是GML
plt.subplot(244)
plt.bar(range(256), histr2)
plt.ylim(0, 0.02)
plt.xlabel("灰度值")
plt.ylabel("各灰度值出现概率")
plt.title("GML规定化直方图")
plt.subplot(245)
plt.axis("off")
plt.imshow(img1, vmin=0, vmax=255, cmap=plt.cm.gray)# 这里的vmin和vmax是灰度值的范围,cmap是灰度图的颜色
plt.title("原图像")
plt.subplot(247)
plt.axis("off")
plt.imshow(equ1, cmap="gray")
plt.title("SML规定化图像")
plt.subplot(248)
plt.axis("off")
plt.imshow(equ2, cmap="gray")
plt.title("GML规定化图像")
plt.savefig("ch03-19_regular.jpg")
plt.show()
# sml的灰度级
print("SML的灰度级:", np.unique(equ1).shape[0])
# gml的灰度级
print("GML的灰度级:", np.unique(equ2).shape[0])3.运行截图
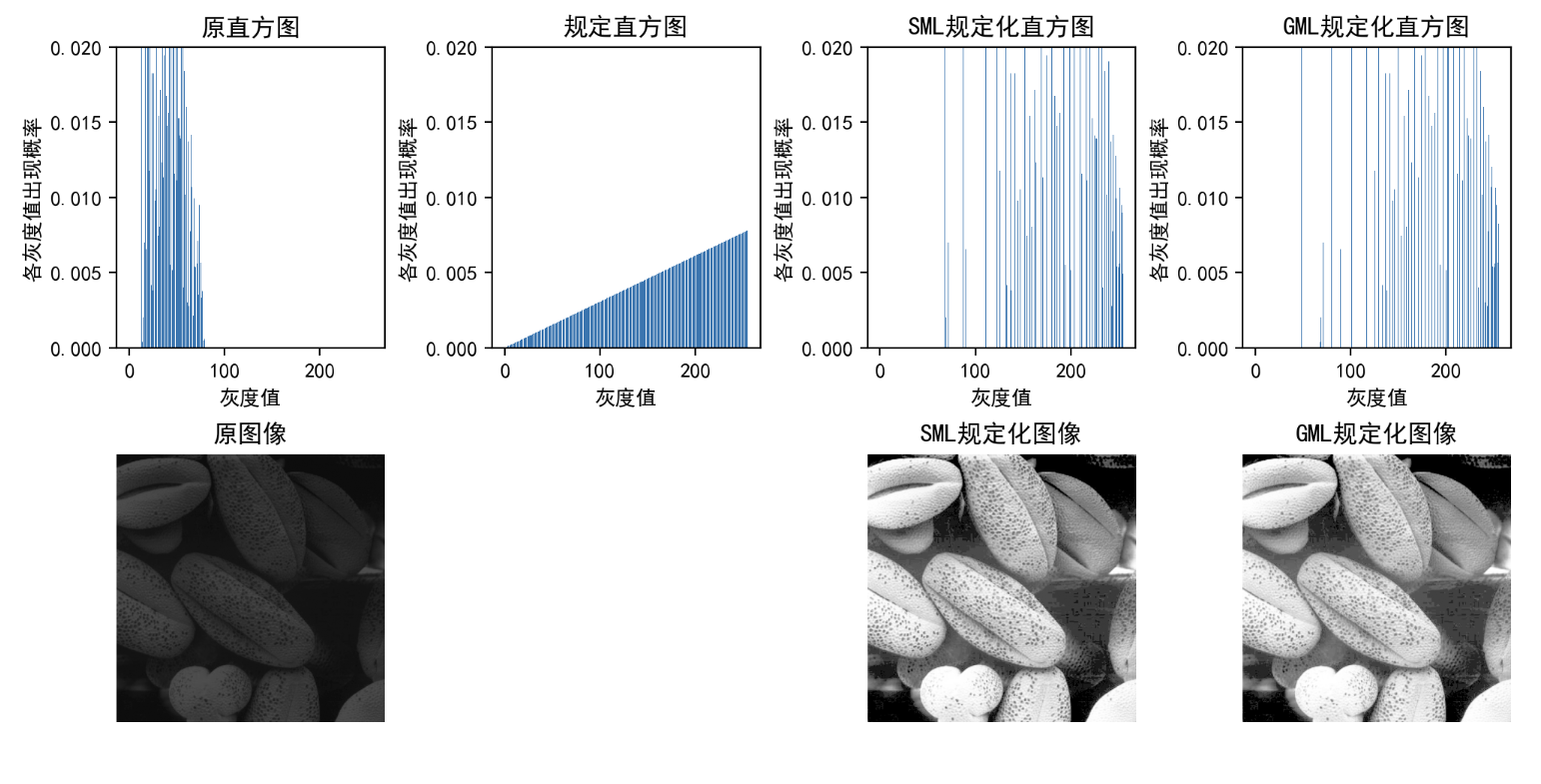
SML映射规则的期望误差大于等于GML映射规则的期望误差,因此,GML映射规则总会得到比SML映射规则更接近规定直方图的结果。
4.直方图规定化是一个需要谨慎使用的工具。它的主要缺点是:
- 全局处理导致细节丢失和颜色失真(尤其对彩色图像)。
- 效果高度依赖目标分布的选择,选择不当会适得其反。
- 可能合并灰度级,降低图像质量。
- 无法处理局部对比度问题。
