数字图像处理

yange大约 9 分钟大数据学科DIP

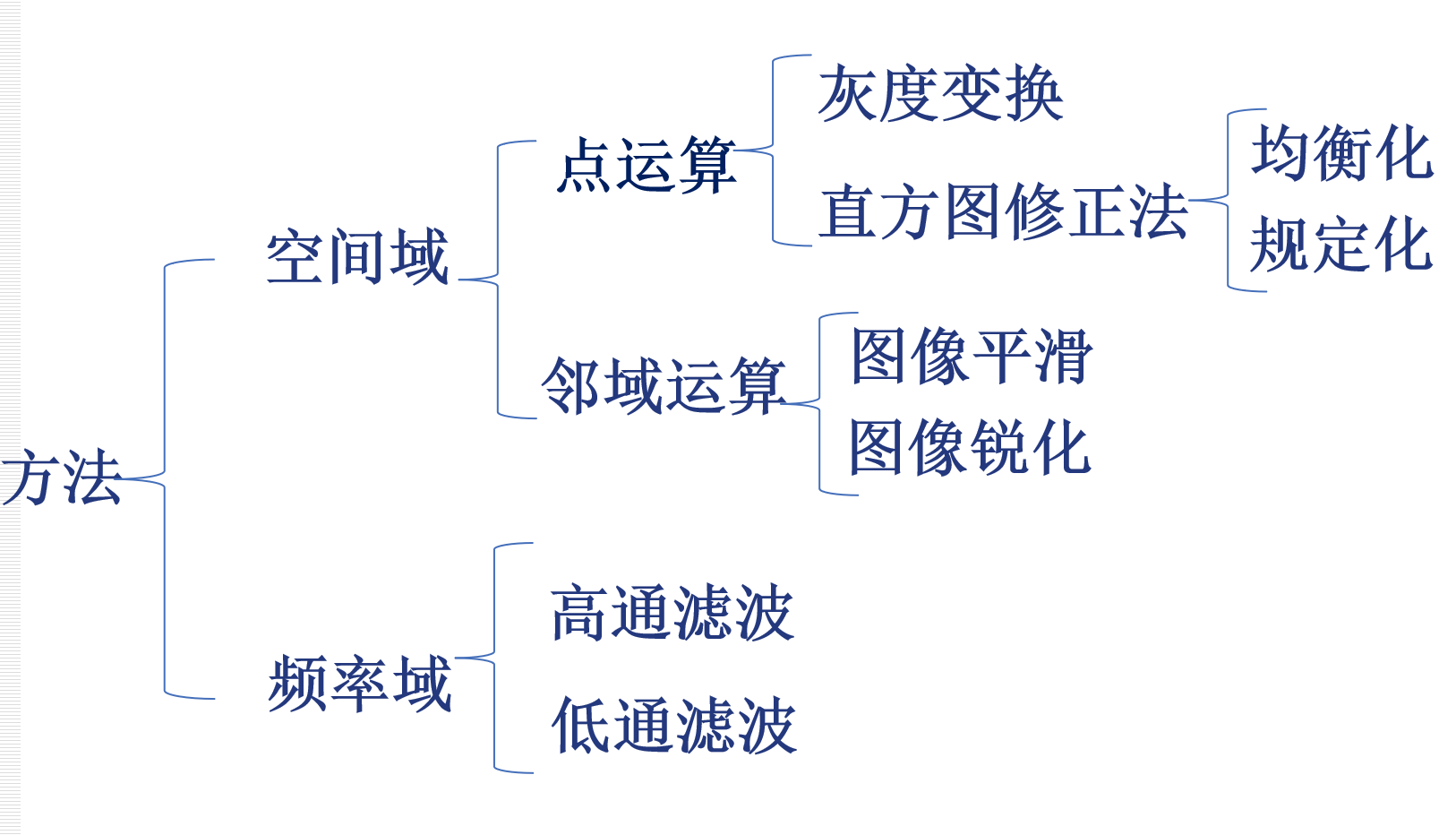
3 图像增强方法

3.1什么是图像增强

前言

定义

图像增强就是让图像变得更有用的过程。

图像增强的特点👇

突出人们感兴趣的部分细节，而压制不感兴趣的细节，并不能增加原始图像的信息，只能增强对某种信息的辩别分析能力；
图像增强是让图像变得更加有用，增强后的图像并不一定趋向原清晰图像。

图像增强的工作包括：

突出图像中有趣的细节
去除图像中的噪音
使图像更具视觉吸引力

图像增强应用的场景：👇

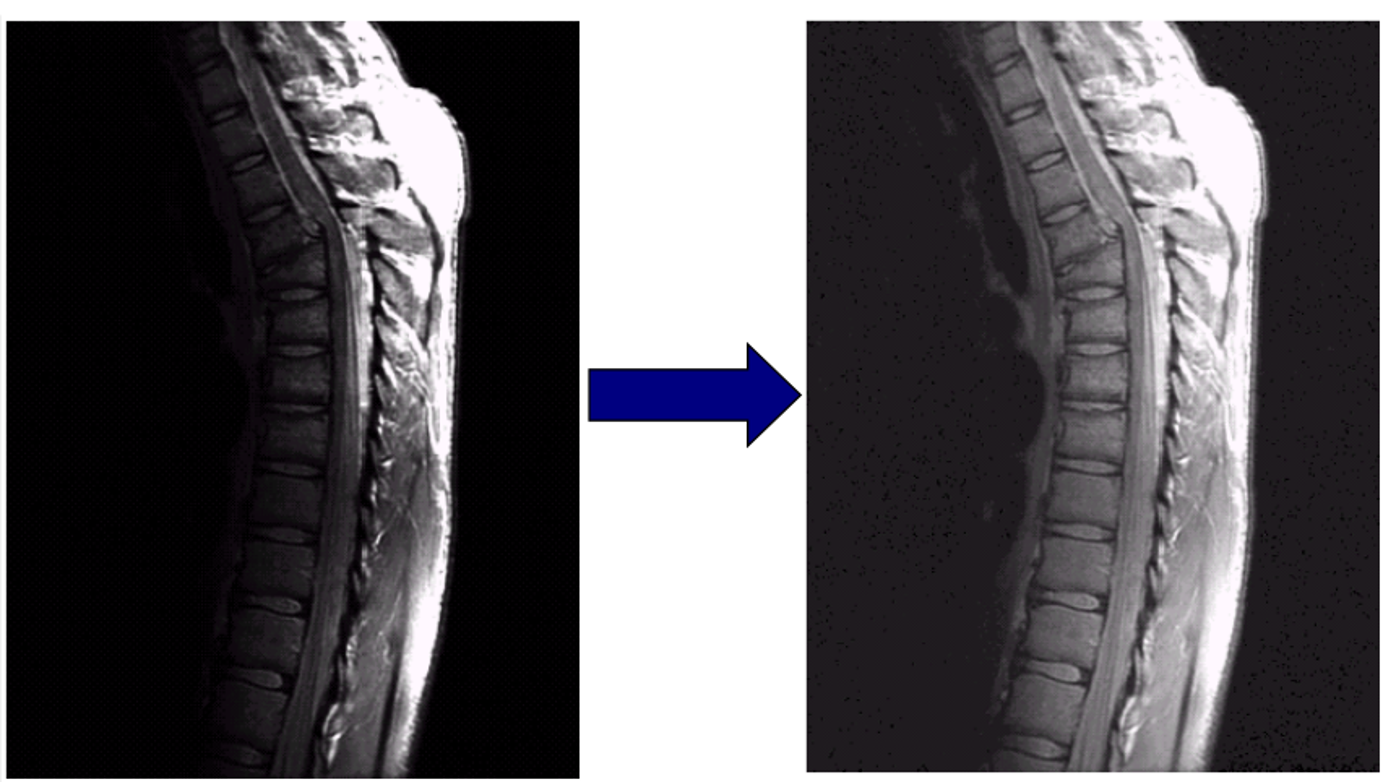
图像增强的分类：

3.2 灰度变换

灰度变换

定义

灰度变换是一种点处理技术，是对像素点的灰度值进行运算，得到像素点的新灰度值。可用以下函数式表示：

s=T(r)

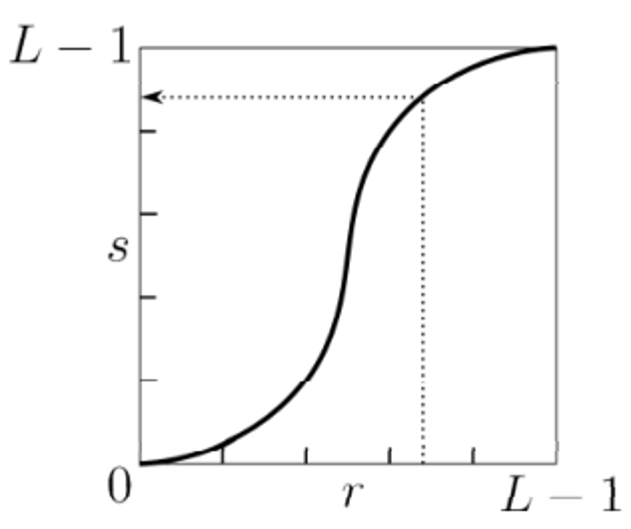
特点：

只跟像素点自身灰度值有关，与邻域像素点灰度值无关
仅改变像素点的灰度值，不改变空间坐标

灰度变换的分类：线性和非线性。

线性灰度变换：

图像反向
阈值化
全局线性变换
分段线性变换
位平面切片

非线性灰度变换：

对数变换
幂律变换
Gamma变换

总结

课堂作业

灰度变换是一种点处理，点处理的特点？
线性灰度变换的斜率小于1时？大小1时？
对数变换常用于什么地方？

3.3 代码实操

前言

准备函数

1. 定义函数

定义函数，统计直方图，全局灰度线性变换，分段线性变换，位平面切片，对数变换，幂次变换，Gamma变换
这些技术都属于图像增强中灰度（像素值）变换的范畴，其核心思想都是通过一个特定的函数 s = T(r)，将原始输入像素值 r 映射为新的输出像素值 s，以改善图像视觉效果或突出所需信息。

#统计直方图
def histogram(image):
    (row, col) = image.shape
    #创建长度为256的list
    hist = [0]*256
    for i in range(row):
        for j in range(col):
            hist[image[i,j]] += 1
    hist=hist/np.sum(hist)
    return hist

# 全局灰度线性变换（也可对彩色图像进行线性变换）
def global_linear_transmation(im,c=0,d=255):
    img=im.copy()
    maxV = img.max()
    minV = img.min()
    if maxV==minV:
        return np.uint8(img)
    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            img[i, j] = ((d-c) / (maxV - minV)) * (img[i, j] - minV)+c#img[i,j]代表的是某像素点三通道的值
    return np.uint8(img)

# 对img_result进行分段线性灰度变换
#lists存放着各段分段前后的灰度范围,每段有4个值【【原起始，原终止，目标起始，目标终止】，【。。。】】
def piecewise_linear_transformation(im,lists): 
    global img_result,img_empty
    try:
        img=im.copy()
        for list in lists:
            a = int(list[0])
            b = int(list[1])
            c = int(list[2])
            d = int(list[3])
            for i in range(img.shape[0]):
                for j in range(img.shape[1]):
                    if(img[i,j]>=a and img[i,j]<=b):
                        img[i, j] = ((d- c) / (b-a)) * (im[i, j] - a)+c
    except:
        showerror("错误提示","灰度值设置不合理，起始灰度值不能与终止值相同")
        img = img_empty
    return img

#位平面分割
def Bit_Plane_Slicing(im):
    img=im.copy()
    BP=np.zeros([8,img.shape[0],img.shape[1]])
    for n in range(8):
        for i in range(img.shape[0]):
            for j in range(img.shape[1]):
                if(img[i,j]>=2**(7-n)):
                    BP[n][i,j]=2**(7-n)
                    img[i,j]=img[i,j]-2**(7-n)
                else:
                    BP[n][i,j]=0
    return BP

#对数变换，默认不改变像素点的范围（0-255）
def logarithmic_transformations(src,a=0,c=1):
    dst=np.zeros([src.shape[0],src.shape[1]])
    for i in range(src.shape[0]):
        for j in range(src.shape[1]):
            dst[i,j]=a+c*math.log(1+src[i,j])
    return np.uint8(dst)

#幂次（伽马）变换
def power_law_transformations(im,gamma=1,c=1):
    img=np.zeros([im.shape[0],im.shape[1]])
    for i in range(im.shape[0]):
        for j in range(im.shape[1]):
            img[i,j]=c*255.0*(im[i,j]/255.0)**gamma
    return np.uint8(img)

全局线性变换

定义：通过线性函数 s = a * r + b 全局调整每个像素值，a 控制对比度，b 控制亮度。
应用场景：简单对比度拉伸、整体亮度调整。

import cv2
import numpy as np
import matplotlib.pyplot as plt

# %matplotlib inline
# %config InlinBackend.figure_format="retina"

plt.rcParams['font.family']=['SimHei'] #用来正常显示中文
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

#全局线性变换
im = cv2.imread(r"./img/rice.tif",0) #读取灰度图像
# 全局线性变换
img1=global_linear_transmation(im,80,200) # 将灰度范围扩展到80-200
img2=global_linear_transmation(im,0,255)# 将灰度范围扩展到0-255
hist1=histogram(img1)#统计直方图
hist2=histogram(img2)#统计直方图

plt.figure(figsize=(6,5))#设置图像大小
plt.subplots_adjust(left=None, bottom=None, right=None, top=None,wspace=0.6, hspace=None)#调整子图间距
plt.subplot(221)#设置子图
plt.axis("off")
plt.imshow(img1, vmin=0, vmax=255, cmap=plt.cm.gray)#显示图像，vmin和vmax设置显示范围，cmap设置显示颜色
plt.title("图片灰度范围窄")
plt.subplot(222)
plt.axis("off")
plt.imshow(img2, vmin=0, vmax=255, cmap=plt.cm.gray)#显示图像，vmin和vmax设置显示范围，cmap设置显示颜色
plt.title("扩展了灰度范围")
plt.subplot(223)
plt.plot(hist1)
plt.ylim(0,0.08)
plt.xlabel("灰度值")
plt.ylabel("概率")
plt.subplot(224)
plt.plot(hist2)
plt.ylim(0,0.08)
plt.xlabel("灰度值")
plt.ylabel("概率")
plt.savefig(r"D:\javasoftware\jupyter_notebook\ch03-3.jpg")#保存图像
plt.show()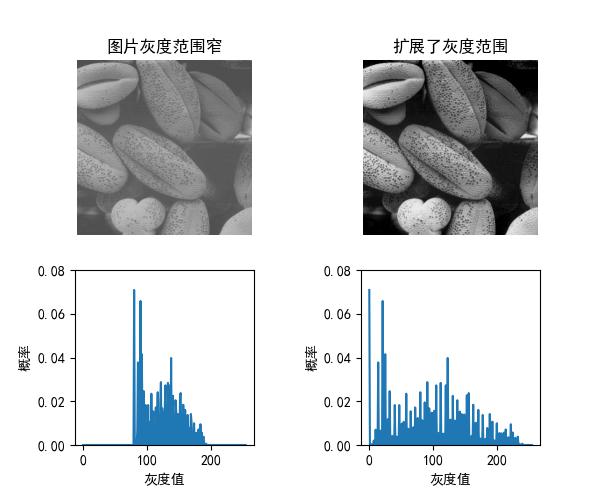

分段线性变换

定义：将灰度范围分成多个区间，每个区间应用不同的线性变换函数。
应用场景：精细对比度调整（如S曲线）、灰度级分层（突出特定目标）。


import cv2
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# %config InlinBackend.figure_format="retina"
plt.rcParams['font.family']=['SimHei'] #用来正常显示中文
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

#分段线性变换
img1 = cv2.imread(r"./img/car1.jpg",0)

img2=piecewise_linear_transformation(img1,[[0,80,0,10],[80,150,10,150],[150,255,150,255]]) # 将灰度范围扩展到80-200


# img3=piecewise_linear_transformation(img1,[[0,100,0,170],[100,255,170,255]])# 将灰度范围扩展到0-255
plt.figure(figsize=(8,4))
plt.subplot(121)
plt.title("原图")
plt.axis("off")
plt.imshow(img1, vmin=0, vmax=255, cmap=plt.cm.gray)
plt.subplot(122)
plt.title("扩展了中间灰度区的图像")
plt.axis("off")
plt.imshow(img2, vmin=0, vmax=255, cmap=plt.cm.gray)

plt.savefig("ch03-6.jpg")
plt.show()

位平面分割

定义：将图像像素值的二进制表示按比特位分解成多个二值平面（如8位图像分解为8个平面）。
应用场景：图像压缩（保留高位平面）、信息隐藏与水印（修改低位平面）。

import cv2
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.family']=['SimHei'] #用来正常显示中文
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

#位平面切片
img0 = cv2.imread(r"./img/bitSlice.jpg",0)
imgSlices=Bit_Plane_Slicing(img0)# 位平面切片

plt.figure(figsize=(10,10))
plt.subplot(331)
plt.imshow(img0,cmap='gray')
plt.title("原图")
plt.axis('off')  #不显示坐标轴
for i in range(8):# # 循环8次，分别显示8个位平面
    plt.subplot(3,3,i+2) #设置子图
    plt.imshow(imgSlices[i],cmap='gray')#显示图像
    plt.title("Bit-plane "+str(7-i))#设置标题
    plt.axis('off')  #不显示坐标轴
    plt.xticks([])#不显示x轴
    plt.yticks([])#不显示y轴

plt.savefig("cbitSlice_out.jpg")
plt.show()

gamma变换

定义：使用 s = c * r^γ 幂律变换，γ值控制对比度调整方向。
应用场景：显示器校正（γ编码）、图像视觉增强（γ<1增强暗部，γ>1增强亮部）。

import cv2
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%config InlinBackend.figure_format="retina"
plt.rcParams['font.family']=['SimHei'] #用来正常显示中文
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

#gamma变换
img0 = cv2.imread(r"./img/Palace.jpg",0) 
img=power_law_transformations(img0,gamma=3,c=1) # 对数变换
img1=power_law_transformations(img,gamma=0.6,c=1)# 对数变换
img2=power_law_transformations(img,gamma=0.4,c=1) # 对数变换
img3=power_law_transformations(img,gamma=0.2,c=1) # 对数变换
plt.figure(figsize=(10,5))
plt.subplot(141)
plt.imshow(img,cmap='gray')
plt.title("原图")
plt.axis('off')  #不显示坐标轴
plt.subplot(142)
plt.imshow(img1,cmap='gray')
plt.title(chr(947)+"=0.6")
plt.axis('off')  #不显示坐标轴
plt.subplot(143)
plt.imshow(img2,cmap='gray')
plt.title(chr(947)+"=0.4")
plt.axis('off')  #不显示坐标轴
plt.subplot(144)
plt.imshow(img3,cmap='gray')
plt.title(chr(947)+"=0.2")
plt.axis('off')  #不显示坐标轴

plt.savefig("ch03-14gamma1.jpg")
plt.show()

总结

变换类型	核心公式	核心思想	主要应用场景	优点	缺点
全局线性变换	`s = a * r + b`	使用统一的线性函数映射所有像素，调整整体的对比度(`a`)和亮度(`b`)。	1. 简单对比度拉伸 2. 整体亮度调整	1. 计算简单，速度快 2. 实现容易	1. 不够灵活 2. 可能造成局部细节丢失
分段线性变换	`s = T₁(r)`, 当 `r` ∈ [r1, r2] `s = T₂(r)`, 当 `r` ∈ [r3, r4]...	将灰度范围划分为多个区间，并在不同区间应用不同的线性函数，进行更有针对性的调整。	1. 精细对比度调整 (如S曲线) 2. 灰度级分层/阈值化 (突出特定目标)	1. 比全局变换灵活得多 2. 可定制化增强特定区域	1. 需要手动选择分段点和参数 2. 复杂度较高
位平面分割	提取每个像素二进制表示的特定位	将图像分解为由各个比特位组成的二值平面，高位包含主要结构信息，低位包含细节和噪声。	1. 图像压缩 (舍弃低位平面) 2. 信息隐藏/数字水印 (修改最低位平面) 3. 图像分析	1. 概念简单清晰 2. 为压缩和隐藏提供了独特思路	1. 不直接用于视觉增强 2. 用于增强时效果有限
对数变换	`s = c * log(1 + r)`	对低像素值（暗部）的扩展幅度远大于高像素值（亮部），用于压缩高动态范围。	1. 显示高动态范围图像 (如傅里叶频谱图、声谱图) 2. 扩展暗部细节	1. 能有效增强暗部细节 2. 防止亮部过曝	1. 变换趋势固定，不可调 2. 应用场景相对专一
Gamma变换 (幂律变换)	`s = c * r^γ`	通过指数γ控制非线性映射。γ<1扩展暗部；γ>1扩展亮部。是最常用的非线性校正和增强方法。	1. 显示设备校正 (核心应用！sRGB标准) 2. 图像视觉增强 (调整对比度、亮度感知)	1. 极其重要且广泛应用 2. 非常灵活，效果可控 3. 符合人眼感知	1. 需要为不同图像和设备选择合适的γ值 2. 概念稍复杂