数据仓库与数据挖掘-第12章节

yange大约 32 分钟大数据学科数仓

导入

今天这几节课，我们要一起探索数据挖掘中两个非常有趣且实用的领域：文本挖掘和时间序列分析。

想象一下，我们平时接触的数据是什么样子的？

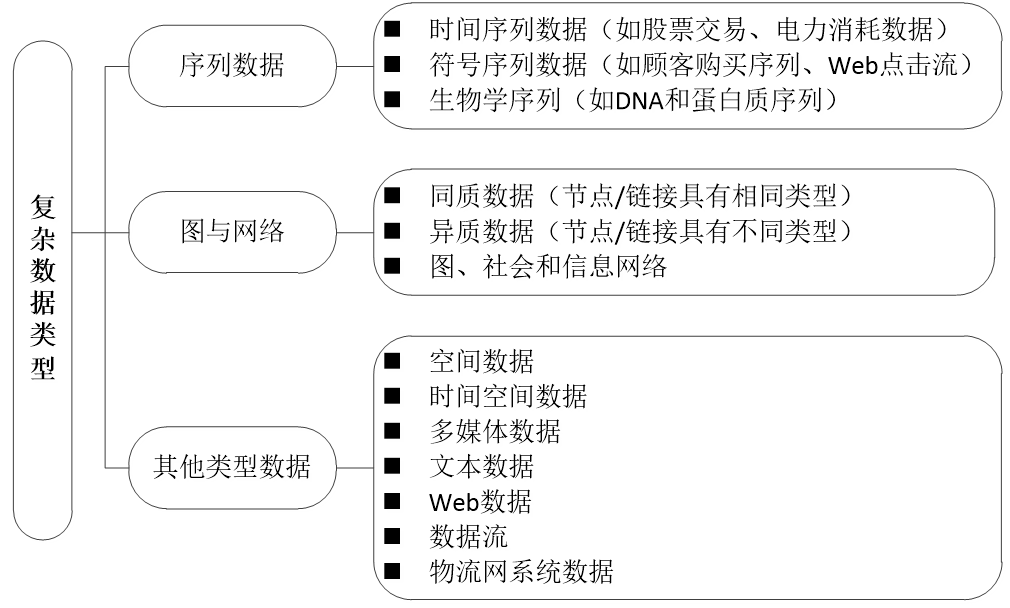
大部分是规整的数字和类别 ，比如销售额、年龄、性别，整整齐齐地躺在表格里，我们称之为结构化数据。但现实中，有海量的数据是“不规整”的，比如社交媒体上的评论、新闻文章、产品描述、我们的聊天记录……这些就是非结构化数据，而其中文本数据占了绝大多数。

1. 文本和时序数据挖掘

1. 文本数据挖掘概要

概要

定义

我们之前学的方法，比如分类、聚类，主要针对“规整”的数据。那么，面对这一堆杂乱无章的、充满人类语言的文本，我们该如何从中挖掘出“金矿”呢？这就是我们今天上半场要解决的问题。

1. 文本挖掘是什么？

简单来说，文本挖掘 就是从大量的文本数据中，通过计算机自动发现以前未知的、有用的、可理解的知识的过程。

把它想象成一个高级的“阅读理解机器人”。这个机器人能快速阅读海量文档（比如一万篇新闻），然后告诉我们：

最近大家都在讨论什么热点话题？（主题发现）
这篇影评是好评还是差评？（情感分析）
这两份研究论文内容上是不是很相似？（文档聚类/分类）

2. 文本挖掘的过程和任务

这个过程就像把原材料（原始文本）加工成一道美味佳肴（有价值的知识）。

第一步：文本获取与预处理

任务：收集原始文本数据，比如从网页上爬取新闻，或者拿到公司内部的客服聊天记录。
好比：去菜市场买菜，把菜洗干净，去掉烂叶子。

第二步：文本清理与分词

文本清理：去除HTML标签、特殊符号、停用词（如“的”、“了”、“是”这些出现频率高但信息量小的词）。
分词：这是中文文本挖掘特有的关键一步！因为英文单词间有空格，而中文没有。比如，“我喜欢数据挖掘”需要被切分成我 / 喜欢 / 数据挖掘。
好比：把洗好的菜切块、切片，准备好下锅。

第三步：特征提取
任务：这是最核心的一步！计算机不认识文字，只认识数字。我们必须把文字转换成它能处理的数学形式（通常是向量）。这就是我们下面要详细讲的 BOW 和 TF-IDF。
好比：给每一道食材（词）赋予一个“味道强度值”，这样计算机就能“品尝”和比较不同的文档了。

第四步：数据挖掘/建模
任务：将上一步得到的数字向量，输入到我们熟悉的算法中，比如分类算法（朴素贝叶斯、SVM）、聚类算法（K-Means）等，进行具体的分析任务。
好比：开火炒菜！根据菜谱（算法模型），将准备好的食材下锅烹饪。

第五步：评估与可视化
任务s：看看模型的效果好不好，比如情感分析的准确率高不高。然后把结果用图表等直观的方式展示出来。
好比s：尝一下菜的味道，调整咸淡，然后精美地摆盘上桌。

3. 文本挖掘的任务

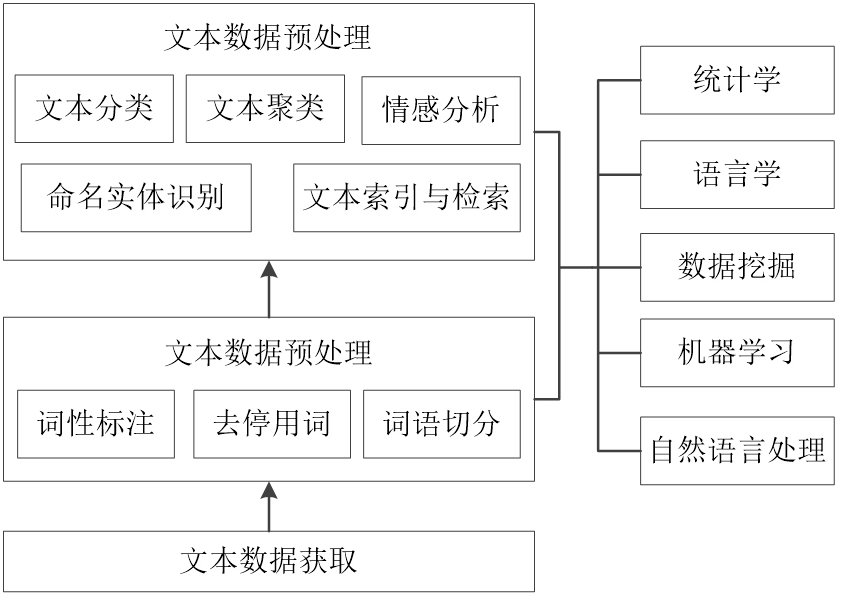
文本挖掘的主要任务有文本分类、文本聚类、主题抽取、文本检索、命名实体识别和情感分析等

通常情况下，文本数据是由若干篇文章或若干条语句构成。一般认为中文词语是最小的语义单元，一句话可以由多个词语组成，而词语可以由一个或者多个汉字组成。
因此，在进行文本分类之前，文本预处理阶段首先应该将文本转化为计算机可以处理的数据结构，也就是将文本切分为构成文本的语义单元，这些语义单元可以是句子、短语、词语或单个字。和英文文本处理分类相比，中文文本预处理更为重要和关键，并且相对复杂。

案例：使用jieba分词

# 安装 jieba（如果未安装）
# !pip install jieba
import jieba
text="我喜欢数据挖掘"
jieba.lcut(text)

输出：
['我', '喜欢', '数据挖掘']

4.2 词性标注与停用词过滤

1. 词性标注

词性标注就是给分词后的每个词语，打上一个表示其词性（Part-of-Speech, POS）的标签。比如，名词（n）、动词（v）、形容词（a） 等等。

输入：我 / 喜欢 / 数据挖掘 / 这门 / 有趣 / 的 / 课程
输出：我/r 喜欢/v 数据挖掘/n 这门/r 有趣/a 的/u 课程/n

这里 r=代词， v=动词， n=名词， a=形容词， u=助词

如果我们想从新闻中提取“谁-做了什么-在哪里”这样的信息，那么名词（人名、地名、机构名）和动词（行为）就是关键。词性标注能帮助我们快速定位这些关键信息。

2. 停用词过滤

停用词是指在文本中出现频率非常高，但本身携带信息量极少的词语。停用词过滤就是在预处理时，将这些词直接剔除。

中文常见停用词：

助词：的、地、得、了、着、过
连词：和、跟、与、同、而、或
介词：在、于、从、向、对、关于
语气词：啊、哦、嗯、吧、呢
标点符号：，。！？ “ ”
一些代词、副词：我、你、他、很、都、就
过滤前：我 / 今天 / 非常 / 喜欢 / 这堂 / 关于 / 数据挖掘 / 的 / 课程
过滤后：今天 / 非常 / 喜欢 / 数据挖掘 / 课程

（去除了“我”、“这堂”、“关于”、“的”这些停用词）

为什么要过滤它们？

降低噪声，提升信号：停用词就像背景噪音。
减少特征维度，提高效率：一个中文停用词表通常有几百到上千个词。直接剔除它们，能显著减少我们特征向量的长度（词典大小），从而降低后续模型计算的开销，提升训练和预测的速度。
提升模型性能：通过去除无关的噪声特征，模型（如分类器）可以更专注于那些有区分度的词汇，从而通常能获得更好的准确率。

思考：这个产品很好” vs “这个产品极其好”，停用词过滤后，还能区分出它们的情感吗？

4.3 文本表征

在文本预处理后，文本由句子变成了词语，但是计算机还无法直接处理词语，因此要将这些词语表示为数据挖掘算法可以处理的形式。常用的文本表征方法有词袋（Bag of Word，BoW）模型和词嵌入（Word Embedding）模型。

4.3.1 词袋模型(Bag of Word) 一种“简单粗暴”的表示法

核心思想：无视顺序，只数个数

请想象一个场景：有一个神奇的“袋子”（Bag），你拿着一篇文档，不管里面的词语是什么顺序，直接把所有词都扔进这个袋子里。然后，你唯一关心的是：这个袋子里，每种词分别出现了多少个？

这就是词袋模型的核心：它完全忽略词语在文档中的语法、语序和上下文关系，只关心两件事：

词表中都有哪些词？
在当前文档里，每个词出现了几次？

举例说明：

文档1： 我喜欢数据挖掘，也喜欢机器学习。

我出现 1 次 -> 1
喜欢出现 2 次 -> 2
数据挖掘出现 1 次 -> 1
机器学习出现 1 次 -> 1
重要出现 0 次 -> 0
分支出现 0 次 -> 0
-----> 文档1的BOW向量：[1, 2, 1, 1, 0, 0]

文档2： 机器学习是数据挖掘的一个重要分支。

我出现 0 次 -> 0
喜欢出现 0 次 -> 0
数据挖掘出现 1 次 -> 1
机器学习出现 1 次 -> 1
重要出现 1 次 -> 1
分支出现 1 次 -> 1
----->文档2的BOW向量：[0, 0, 1, 1, 1, 1]

两篇原本是文字的文档，被成功地表示成了两个数字向量。这两个向量的长度等于词表的大小（这里是6）。我们可以用这些向量来计算文档间的相似度，或者输入给机器学习模型（如分类器）。

思考：我吃苹果，和苹果吃我？它们的BOW向量是一样的吗？合理吗？

4.3.2 词频-逆文档频率（TF-IDF） ----- 给词语加上“重要性”权重

核心思想：一个词的重要性，与它在当前文档中出现的频率成正比，与它在整个文档集合中出现的频率成反比。

公式：
TF-IDF：TF-IDF(词, 文档) = TF(词, 文档) * IDF(词)

TF（词频）：衡量一个词在当前文档中有多重要。TF(词, 文档) = (词在文档中出现的次数) / (文档中的总词数)
IDF（逆文档频率）：衡量一个词有多常见。越常见的词，权重越低。IDF(词) = log(文档集合中的文档总数 / (包含该词的文档数 + 1))

通俗理解：TF-IDF的聪明之处在于，它打压了“到处可见”的“普通词”，抬高了“独具特色”的“专业词”。

TF-IDF的优点是简单快速，易于理解，但是只用词频衡量文档中词的重要性还是不够全面，无法体现词在上下文中的重要性。因此虽然BoW和TF-IDF在各自方面都很受欢迎，但在理解文字背景方面仍然存在空白。因此又出现了Word2Vec、CBOW、Skip-gram等词嵌入技术。

python案例：👇

# 安装 jieba（如果未安装）
# !pip install jieba

import jieba
from sklearn.feature_extraction.text import TfidfVectorizer

# 定义中文分词函数
def chinese_tokenizer(text):
    return list(jieba.cut(text))

# 定义3个中文文档
documents = [
    "我喜欢自然语言处理",
    "自然语言处理很有趣",
    "我喜欢机器学习"
]

# 使用 jieba 分词 + TF-IDF
tfidf_vectorizer = TfidfVectorizer(tokenizer=chinese_tokenizer)
tfidf_matrix = tfidf_vectorizer.fit_transform(documents)

# 获取词汇表
feature_names = tfidf_vectorizer.get_feature_names_out()

# 转换为 DataFrame
df_tfidf = pd.DataFrame(
    tfidf_matrix.toarray(),
    columns=feature_names,
    index=[f"文档{i+1}" for i in range(len(documents))]
)

print("词汇表（分词后）:", feature_names)
print("\nTF-IDF 矩阵（分词后）:")
display(df_tfidf)

4.4 文本分类--给文本贴标签的“智能秘书”

文本分类的定义

文本分类是典型的监督学习任务。其目标是：根据一个已经被标注好类别的训练集（例如，已知哪些是体育新闻，哪些是财经新闻），构建一个分类模型，从而能够自动为新的、未知的文本分配一个或多个预定义的类别标签。

2. 典型应用场景

垃圾邮件过滤 ：二分类问题，判断邮件是“垃圾邮件”还是“正常邮件”。
新闻主题分类 ：多分类问题，将新闻自动归类到“体育”、“财经”、“科技”、“娱乐”等板块。
情感分析 ：判断一条评论或微博的情感倾向是“正面”、“负面”还是“中性”。
语言识别 ：判断一篇文章是用什么语言写的（如中文、英文、法文）。

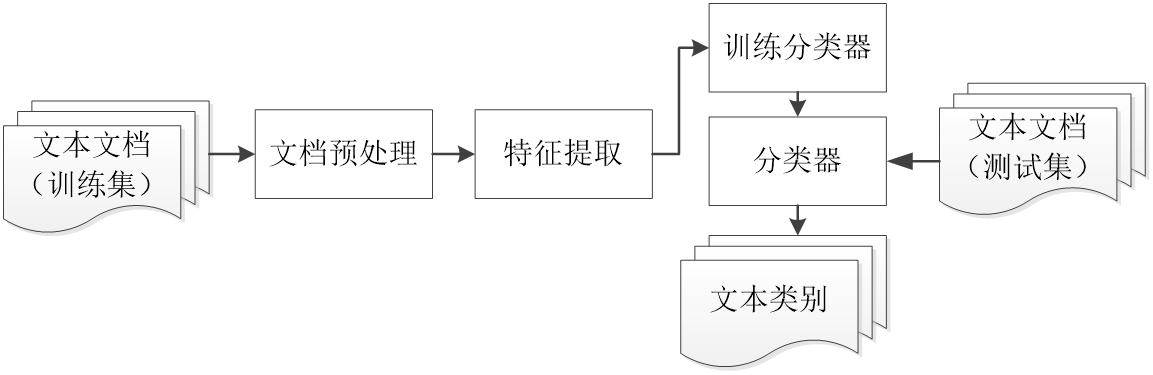
3. 基本流程 👇

准备训练数据：收集大量文本，并人工为其打上正确的标签。这是监督学习的基础。
文本预处理与特征提取：就是我们前几节课讲的内容！对训练文本进行分词、去停用词，并用BOW或TF-IDF将其转换为特征向量。
模型训练：将特征向量和对应的标签输入到分类算法中，训练出一个分类模型。
- 常用算法：
  - 朴素贝叶斯：非常经典高效，尤其适合文本数据，假设特征（词语）之间相互独立。
  - 支持向量机：效果强大，擅长处理高维数据。
  - 逻辑回归：简单易懂，同样是非常优秀的基线模型。
  - 深度学习模型：如CNN、RNN、BERT等，能捕捉更复杂的语义特征，但需要更多数据和时间。
预测新文本：当新的文本到来时，同样进行预处理和特征提取，然后使用训练好的模型预测其类别。

核心特点：有师学习，需要带标签的训练数据。

4.5 文本聚类发现文本中的“自然群落”

1. 定义

文本聚类是典型的无监督学习任务。其目标是：在没有任何先验标签的情况下，完全根据文本内容本身的相似性，将文档集合自动划分成若干个簇（Cluster），使得同一个簇内的文档彼此相似，不同簇间的文档差异较大。

打个比方：它像一个具有洞察力的市场分析师，面对一堆零散的客户反馈，没有人告诉他有哪些类别。他通过阅读和分析，自动发现这些反馈可以聚成几类：比如“抱怨物流问题的”、“称赞产品质量的”、“咨询售后服务的”。

2. 典型应用场景

主题发现 ：从大量新闻或学术论文中，自动发现潜在的热门主题。
用户画像 ：根据用户的搜索记录、评论内容等，将用户划分为不同的兴趣群体。
文档归档 ：对公司内部大量未分类的文档进行自动整理归纳。
结果分组 ：搜索引擎将相似的搜索结果归为一组，提升用户体验。

3. 基本流程: 👇

准备无标签数据 ：收集需要分析的文本集合，不需要任何人工标注。
文本预处理与特征提取 ：与分类相同，将文本转换为TF-IDF等特征向量。
聚类算法建模 ：将特征向量输入聚类算法。
- 最常用算法 ：K-Means聚类。你需要事先指定想要将数据聚成几类（K值）。
- 其他算法 ：层次聚类（不需要指定K值，会形成一棵聚类树）、DBSCAN（能发现任意形状的簇）。
结果分析 ：聚类完成后，需要人工分析每个簇的关键词（如计算簇内词的TF-IDF均值），来理解和解释每个簇代表的“主题”或“含义”。

核心特点：无师学习，探索性分析，结果需要人工解释。

4.6 文本可视化：让数据“自己说话”

文本可视化将文本数据中蕴含的、难以直接观察的规律、模式和关系，通过图形化的手段直观地呈现出来。正所谓“ 一图胜千言 ”，它能让复杂的分析结果一目了然。

3.时序数据挖掘

时序数据挖掘

定义

随着云计算和物联网等技术的发展，时间序列数据的数据量急剧膨胀。高效分析时间序列数据，使之产生业务价值成为一个热门话题。时间序列分析广泛应用于股票价格、广告数据、气温变化、工业传感器数据、个人健康数据、服务器系统监控数据和车联网等领域中。

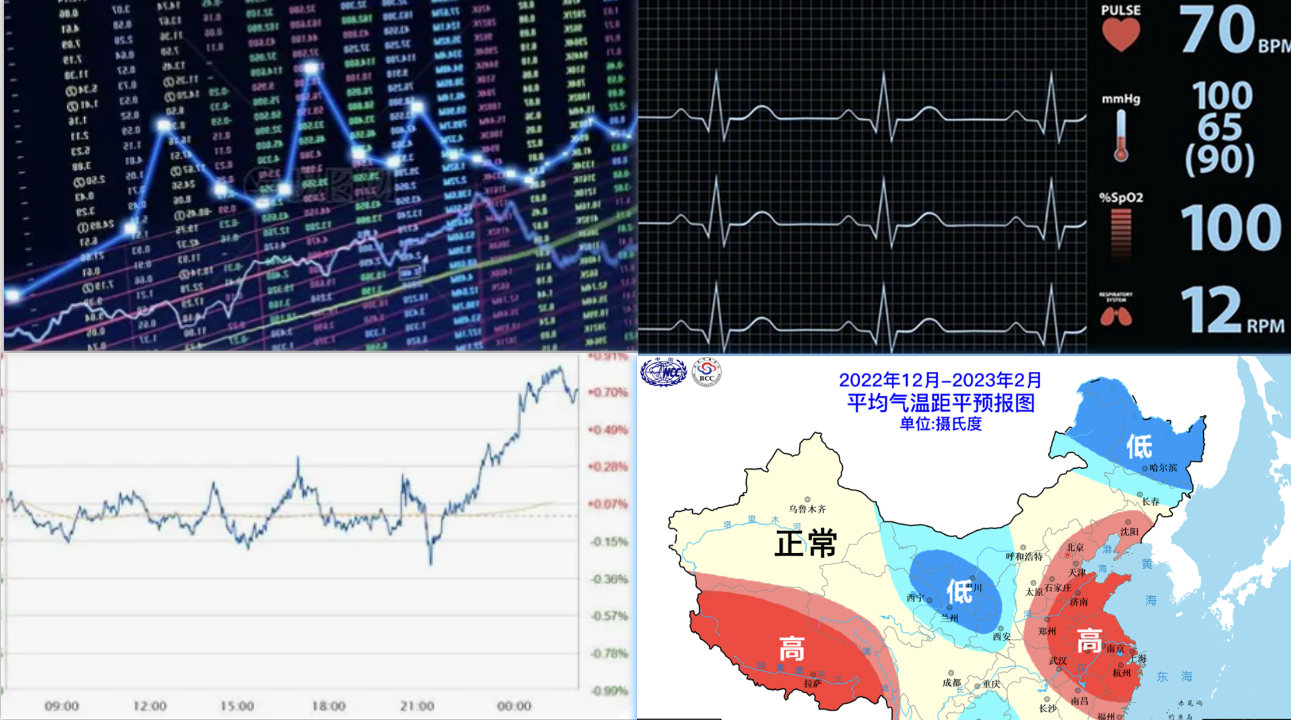
0.为什么要学习时序数据分析？

适配海量动态数据场景 ：现实中大量数据自带时间属性，比如股票价格、气温变化、用户行为轨迹、设备运行状态等，普通挖掘方法无法体现 “时间先后” 的关联价值，而时间序列分析正是针对这类数据的专属工具。
支撑预测与决策需求 ：这是最核心的实用价值，通过分析历史时间序列的规律（如趋势、周期性、季节性），可实现未来预测，比如企业销量预测、交通流量预警、疫情传播趋势判断，直接为决策提供数据支撑。
补充传统数据挖掘的短板 ：传统分类、聚类算法多假设数据独立分布，而时间序列数据存在 “时序相关性”（如今天的气温与昨天相关），时间序列分析能处理这种依赖性，避免模型失真，让分析结果更贴合实际。

1. 时间序列和时间序列分析

1.1. 时间序列

一个时间序列过程定义为一个随机过程，是指一个按时间排序的随机变量的集合，其中T是索引集合，表示定义时序过程以及产生观测值的一个时间集合。

比如：某股票在一天内每分钟的价格，某网站在一天内每分钟的访问量，某城市在一年内每个月的降雨量等。

时间序列可以分为平稳序列和非平稳序列。

平稳序列是指基本上不存在长期趋势的序列，各观测值基本上在某个固定的水平上波动，或虽有波动，但并不存在某种规律。

非平稳序列是指有长期趋势、季节性和循环波动的复合型序列，其趋势可以是线性的，也可以是非线性的。

1.2. 时间序列分析

时间序列分析是一种动态数据处理的统计方法，该方法基于随机过程理论和数理统计学方法，研究随机数据序列所遵从的统计变化规律，以解决实际问题。通常影响时间序列变化的要素有长期趋势、季节变化、循环波动和随机因素。

长期趋势（T） ：是时间序列在长时期内呈现出来的持续向上或持续向下的变动。
季节变动（S） ：是时间序列在一年内重复出现的周期性波动。
循环波动（C） ：是时间序列呈现出的非固定长度的周期性变动。
随机因素（I） ：是时间序列中除去长期趋势、季节变动和循环波动之后的随机波动。不规则波动通常总是夹杂在时间序列中，致使时间序列产生一种波浪形或震荡式的变动。

2. 时间序列平稳性和随机性判定

上节课我们讲到，时间序列是按时间顺序记录的数据点。我们的核心目标是从过去的数据中找出规律，预测未来。但并不是所有序列都“乖乖听话”，可以直接被预测。我们首先要判断它的“脾气秉性”，而最重要的两个性格特征就是平稳性和随机性。

2.1. 时间序列的平稳性”

平稳性是时间序列的一个属性，一个平稳的时间序列指的是这个时间序列和时间无关，也就是说，如果一个时间序列是平稳的，那么这个时间序列的统计量均值、方差和自相关系数都是一个常数，和时间无关。

在做时间序列分析时，经常要对时间序列进行平稳性检验。用Python来进行平稳性检验主要有时序图检验、自相关图检验以及构造统计量进行检验3种方法。

其实这3中方法本质是 “直观观察→统计特征→量化验证 ” 层层递进，确保时序数据满足建模前提，避免后续分析出现偏差。

（1）时序图检验：直观判断整体趋势

定义：就是普通的时间序列图，即以时间为横轴，观察值为纵轴进行检验。利用时序图可以粗略观察序列的平稳性。
作用：直接绘制 “时间→数据值” 的折线图，快速观察数据是否有明显趋势（如持续上升 / 下降）、季节性（如每月固定波动）或突变点。
必要性：如果时序图能直接看到趋势 / 季节性，说明数据大概率非平稳，无需复杂计算就能初步判断，是最快捷的 “初筛工具”。

import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_excel('Bike_count.xls', index_col='Date', parse_dates=True) # 读取数据，设置索引为日期，并解析日期格式
fig = plt.figure(figsize=(10,5), dpi=100)
from matplotlib.dates import DateFormatter
plt.gca().xaxis.set_major_formatter(DateFormatter('%m-%d-%H')) # 设置x轴时间格式
plt.xticks(pd.date_range(data.index[0],data.index[-1],freq='3H'), rotation=45) # 设置x轴刻度
plt.plot(data['Total'])# 绘制时序图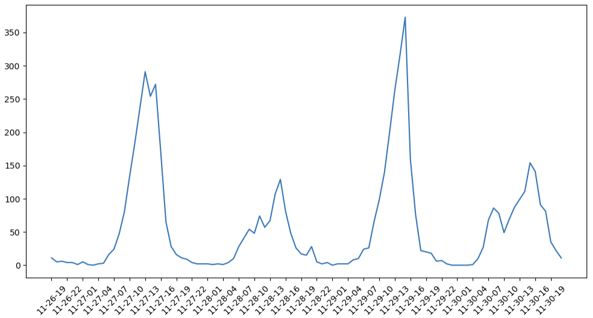

数据走势没有明显趋势或周期，基本可以视为平稳序列，但还需要利用自相关图进一步验证。

（2）自相关图检验

自相关函数（autocorrelation function，ACF）描述的是时间序列观测值与其过去的观测值之间的线性相关性，表达式如式如下所示。

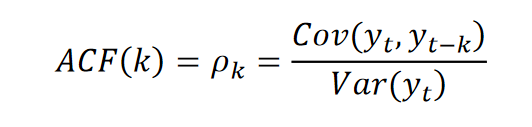
偏自相关函数（partial autocorrelation function，PACF）描述的是时间序列观测值与其过去的观测值之间的非线性相关性。

1. 先搞懂：什么是“相关性”？
相关性（Correlation）就是两个东西一起变化的程度。
比如，“冰淇淋销量”和“气温” 通常是正相关的（天热，冰淇淋卖得多）。
在时间序列里，我们关心的是 “今天的数据”和“过去某天的数据” 有没有关系。

2.ACF自相关函数
ACF是“今天的数据”和“过去若干天的数据”的相关性。
假设你记录了每天的气温，你想知道：
“今天的气温”和“昨天的气温” 有多相关？（ACF(1)）
“今天的气温”和“前天的气温” 有多相关？（ACF(2)）
“今天的气温”和“10 天前的气温” 有多相关？（ACF(10)）
如果 ACF(1) = 0.8，说明今天的气温和昨天的气温高度相关（昨天热，今天也可能热）。
如果 ACF(10) ≈ 0，说明 10 天前的气温对今天基本没影响。

3.PACF偏自相关函数
PACF 是“今天的数据”和“过去某天的数据”的相关性，但 去掉了中间那些天的干扰。
今天的气温”和“3 天前的气温” 有多相关？（PACF(3)）
但是！不能直接看 ACF(3)，因为 ACF(3) 里包含了 2 天前、1 天前的影响。
3 天前的气温可能影响 2 天前、1 天前的气温，进而影响今天的气温。
PACF(3) 会“过滤掉” 2 天前、1 天前的影响，只看 3 天前和今天的直接关系。

4.拖尾和截尾

拖尾是 ACF 和 PACF 的共同特点，它们的图形在某个滞后期之后会逐渐变为 0。
截尾是突然 “截止” 的意思，意味着 “截止到某个滞后期，相关性为 0”。

from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
plt.rcParams['font.family'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# plt.subplot(2,1,1)
plot_acf(data.Total) #生成自相关图
plt.xlabel('滞后期数')
plt.ylabel('自相关系数')
# plt.subplot(2,1,2)
plot_pacf(data.Total) #生成偏自相关图
plt.xlabel('滞后期数')
plt.ylabel('偏自相关图')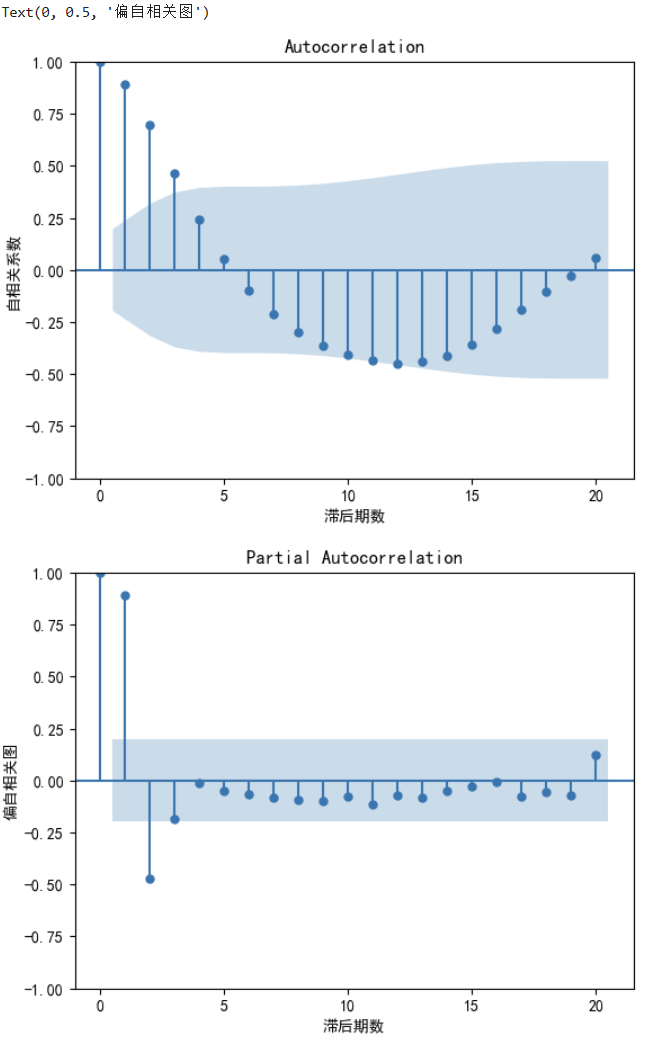

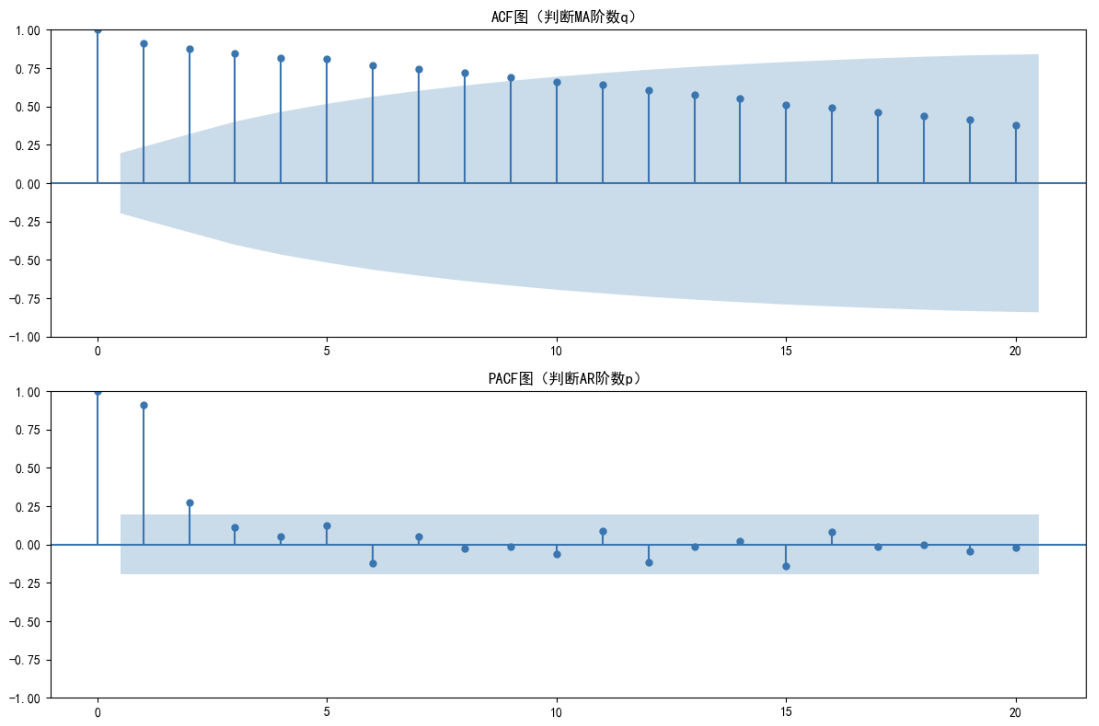
ACF：自相关系数，描述时间序列在时间上的依赖性。判断MA(q)值
PACF：偏自相关系数，描述时间序列在时间上的相关性。判断AR(p)值
首选：AR(1)模型（p=1, q=0）依据：PACF在1阶截尾更明显，因此q=1;ACF是拖尾，不用考虑阶数q=0

（3）构造统计量

利用绘图判断序列的平稳性比较直观，但不够精确，ADF（Augmented Dickey-Fuller）法直接通过假设检验的方式来验证平稳性。通过构建统计量（如 ADF 的 t 统计量、LB 的卡方统计量）和对应的 p 值，从概率角度 “量化判断” 数据是否平稳。

2.2 时间序列纯随机性检验

如果时间序列值之间没有相关性，即意味着该序列是一个没有记忆的序列，过去的行为对将来的发展没有任何影响，这种序列被称为纯随机序列。从统计分析的角度，纯随机序列是没有任何分析价值的序列。因此，为了确定平稳序列的分析价值，需要进行纯随机性检验。

如果一个时间序列满足：

每个数据点都是 “独立的”：比如今天的数值和昨天、前天、上个月的数值毫无关系；
没有任何规律：既没有上升 / 下降趋势，也没有季节性（比如每月波动），更没有周期性；
就像 “无头苍蝇” 乱撞：下一个数值完全随机，没法通过历史数据预测。

这种序列就是「纯随机序列」，也叫 “白噪声序列”（比如完全随机生成的一串数字）

为什么要做纯随机性检验？

别在 “无用数据” 上浪费时间。如果检验结果是纯随机序列，直接放弃深入分析（比如预测、找规律），节省时间和精力。

Q统计量和LB统计量都用来检验序列是否纯随机，LB 是 Q 的改进版，更精准、适用场景更广。

原理：🍐

不用记公式！记住核心思路：“把多个自相关系数‘打包’成一个指标，判断是否全为 0 。

1. 类比理解：班级成绩是否 “全是随机分”
假设要判断一个班级的成绩是不是 “纯随机打分”（对应序列是否纯随机）：
第一步：看每个学生的成绩和其他人的相关性（对应 “自相关系数”：比如第 1 名和第 2 名、第 1 名和第 3 名的分数关联）；
第二步：把所有 “相关性” 汇总成一个 “综合分数”（对应 Q/LB 统计量）；
第三步：如果这个 “综合分数” 太高，说明成绩不是随机的（有规律，比如学霸分数都高）；如果太低，说明是随机的（没规律）。

2. 对应到统计量的核心逻辑：
对于时间序列，我们先算前 k 个 “自相关系数”（比如 k=10：看 t1 和 t2、t1 和 t3……t1 和 t11 的关联）；
Q 统计量：把这 k 个自相关系数的平方加起来，再乘以样本量 n（简单粗暴的 “打包”）；
LB 统计量：在 Q 的基础上，加了一个 “修正因子”——(n+2)/(n-j)（j 是自相关系数的滞后阶数），相当于 “校准了样本量小的误差”。

python案例：👇

# 1. 导入所需库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.stats.diagnostic import acorr_ljungbox  # LB统计量检验函数
from statsmodels.tsa.stattools import adfuller  # 平稳性检验（辅助验证）

# 2. 设置中文显示（避免图表乱码）
plt.rcParams['font.family'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 3. 生成两类测试序列
## 3.1 生成纯随机序列（白噪声序列，无规律）
np.random.seed(42)  # 固定随机种子，结果可复现
random_seq = pd.Series(np.random.normal(loc=0, scale=1, size=100))  # 100个服从正态分布的随机数
random_seq.index = pd.date_range(start='2023-01-01', periods=100, freq='D')  # 日度时间索引

## 3.2 生成非纯随机序列（含趋势+轻微波动，有规律）
trend_seq = pd.Series([i*0.5 + np.random.randint(-2, 3) for i in range(100)])  # 线性趋势+小波动
trend_seq.index = pd.date_range(start='2023-01-01', periods=100, freq='D')  # 日度时间索引

# 4. 可视化两类序列（直观对比）
plt.figure(figsize=(12, 6))

# 4.1 纯随机序列图
plt.subplot(2, 1, 1)
plt.plot(random_seq, color='blue', linewidth=1)
plt.title('纯随机序列（白噪声）', fontsize=12)
plt.xlabel('时间')
plt.ylabel('数值')
plt.grid(alpha=0.3)

# 4.2 非纯随机序列图
plt.subplot(2, 1, 2)
plt.plot(trend_seq, color='red', linewidth=1)
plt.title('非纯随机序列（含线性趋势）', fontsize=12)
plt.xlabel('时间')
plt.ylabel('数值')
plt.grid(alpha=0.3)

plt.tight_layout()
plt.show()

# 5. 纯随机性检验（LB统计量）
## 5.1 对纯随机序列检验
lb_random = acorr_ljungbox(random_seq, lags=10)  # lags=10：取前10个滞后期
print("="*50)
print("纯随机序列的LB检验结果：")
print(lb_random)  # 输出包含LB统计量（lb_stat）和P值（lb_pvalue）的DataFrame

## 5.2 对非纯随机序列检验
lb_trend = acorr_ljungbox(trend_seq, lags=10)
print("\n" + "="*50)
print("非纯随机序列的LB检验结果：")
print(lb_trend)

# 6. 结果汇总（简化解读）
print("\n" + "="*50)
print("检验结果汇总：")
print(f"纯随机序列 - LB统计量均值：{lb_random['lb_stat'].mean():.2f}，P值均值：{lb_random['lb_pvalue'].mean():.2f}")
print(f"非纯随机序列 - LB统计量均值：{lb_trend['lb_stat'].mean():.2f}，P值均值：{lb_trend['lb_pvalue'].mean():.6f}")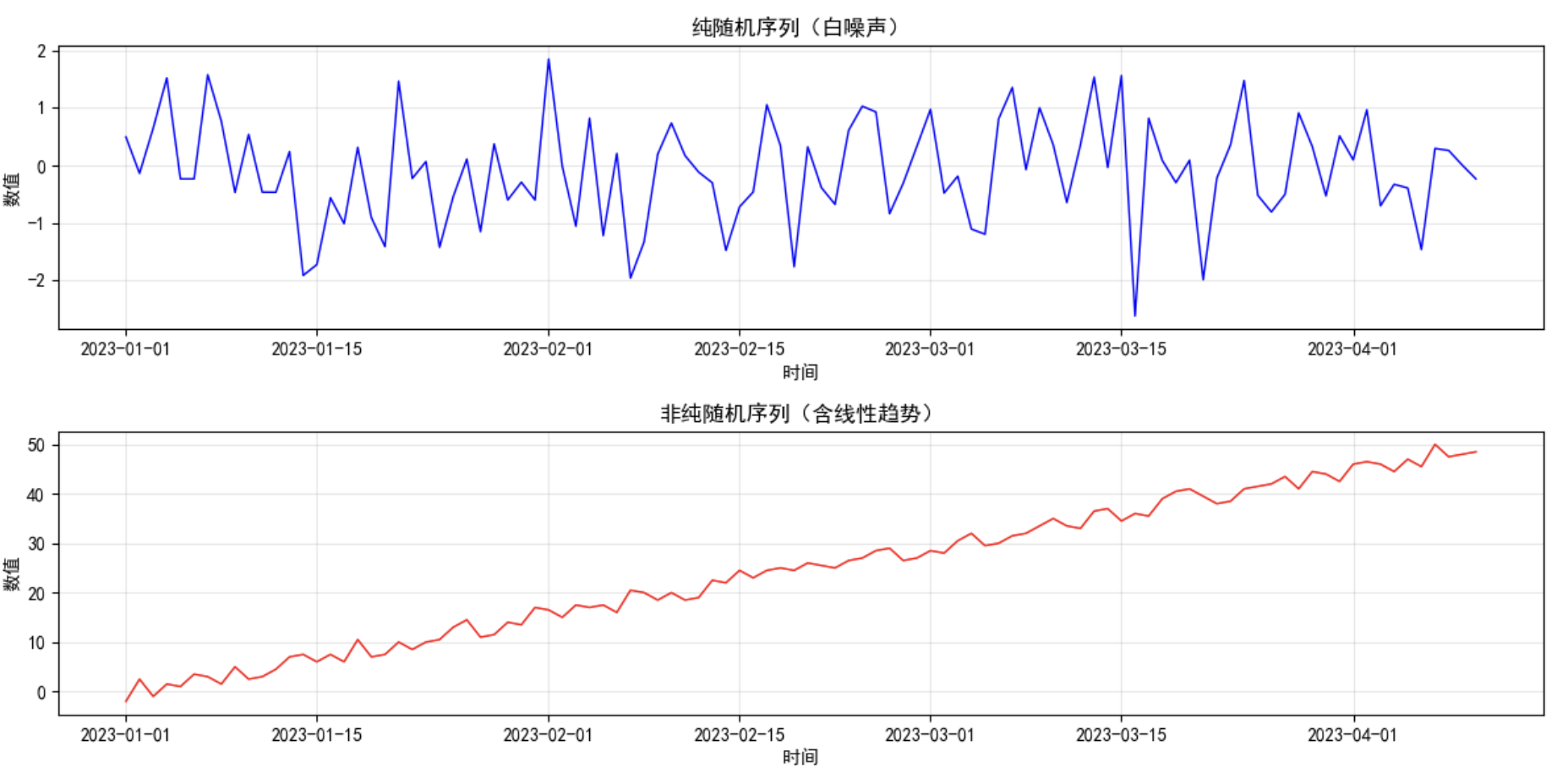

结论：👇

序列类型	检验核心结果	最终结论（是否有分析价值）
纯随机序列	P 值均值 = 0.74（远≥0.05）	无分析价值（无需建模）
非纯随机序列	P 值均值 = 0.000000（远 < 0.05）	有分析价值（可继续建模）

与传统阈值的对比：

p值范围	统计结论	证据强度
p > 0.1	→ 接受白噪声假设	✅ 较强证据
p > 0.05	→ 接受白噪声假设	✅ 标准证据
p > 0.4	→ 强烈接受白噪声假设	✅✅ 很强证据
p < 0.05	→ 拒绝白噪声假设	❌ 序列有规律

2.3 自回归滑动平均ARMA模型

序列类型	平稳性	随机性	例子	是否可预测
平稳非白噪声	✅ 平稳	❌ 非纯随机气温变化、股票收益率	✅ 可预测
平稳白噪声	✅ 平稳	✅ 纯随机	完全随机数	❌ 不可预测
非平稳非白噪声	❌ 非平稳	❌ 非纯随机	GDP增长趋势	⚠️ 需先平稳化
非平稳白噪声	❌ 非平稳	✅ 纯随机	带趋势的随机游走	❌ 不可预测

一个序列经过预处理被识别为平稳非白噪声序列，说明该序列是一个蕴涵相关信息的平稳序列。通常是建立一个线性模型来拟合该序列的发展，以此提取序列中的有用信息。

ARMA 模型的作用就是：用一个简单的线性模型，“捕捉” 这个序列的内在规律，然后用这个规律做预测。

比如用过去 10 天的气温数据拟合模型，预测未来 3 天的气温；用过去 1 个月的销量数据建模，预测下一周的销量。

ARMA模型本质上是一个模型族，可以细分为AR模型、MA模型和ARMA模型三大类。

自回归模型 AR (p)：“用过去的自己预测现在”，比如用昨天和前天的气温预测今天的气温；

现在 = 过去的加权和 + 误差

移动平均模型 MA (q)：“用过去的误差修正现在”，比如用昨天的气温误差预测今天的气温；

现在 = 均值 + 过去误差的加权和

自回归移动平均模型 ARMA (p,q)：“用过去的自己和误差预测现在”，比如用昨天和前天的气温误差预测今天的气温。

现在 = 过去自身 + 过去误差 + 新误差

ARMA模型建模流程如图下所示：

ARMA 是平稳非白噪声序列的 “规律捕捉工具”，AR 靠过去的自己、MA 靠过去的误差、ARMA 两者结合，核心是 “定阶→拟合→检验→预测”，搞定这四步就能用历史数据推未来！

2.4 差分整合移动平均自回归ARIMA模型

上节课学的 ARMA 模型有个 “软肋”：只能处理平稳非白噪声序列（没有趋势、没有季节性）。但现实中，大部分时间序列都是 “不平稳” 的 —— 比如逐年增长的销售额、夏季高峰的用电量、节假日波动的客流量（有趋势 / 季节性）。

ARIMA 模型的作用就是：解决非平稳序列的预测问题—— 它先通过 “差分” 把非平稳序列变成平稳序列，再用 ARMA 模型拟合规律，最后反向还原预测结果。

简单说：ARIMA = ARMA + 差分整合，是 ARMA 模型的 “升级款”，适用范围更广（平稳、非平稳序列都能处理），是时间序列预测的 “万能基础工具”。

python案例：👇

我们用北京市2023年1月1日-4月10日的日平均气温数据（共100天），目标是：

用ARMA模型捕捉气温的时间相关性规律
预测未来5天的日平均气温

# 1. 导入核心库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller  # 平稳性检验
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf  # 定阶
from statsmodels.tsa.arima.model import ARIMA  # ARMA模型（d=0）
from statsmodels.stats.diagnostic import acorr_ljungbox  # 残差检验
import warnings
warnings.filterwarnings('ignore')  # 忽略无关警告


# 2. 准备数据（模拟北京市日平均气温数据，单位：℃）
# 生成逻辑：基础趋势+季节波动+随机噪声（模拟真实气温特征）
np.random.seed(42)
dates = pd.date_range(start='2023-01-01', periods=100, freq='D')  # 100天数据
trend = np.linspace(-5, 15, 100)  # 基础升温趋势（1月到4月）
seasonal = 3 * np.sin(np.linspace(0, 4*np.pi, 100))  # 小幅周度波动
noise = np.random.normal(0, 1.5, 100)  # 随机噪声
temp_data = trend + seasonal + noise  # 合成气温数据
temp_series = pd.Series(temp_data, index=dates, name='日平均气温')

# 查看数据前5行
print("气温数据前5行：")
print(temp_series.head())


# 3. 可视化原始数据
plt.figure(figsize=(12, 4))
plt.plot(temp_series, color='blue')
plt.title('北京市日平均气温时间序列（2023.1-2023.4）', fontsize=14)
plt.xlabel('日期')
plt.ylabel('气温（℃）')
plt.grid(alpha=0.3)
plt.show()


# 4. 步骤1：平稳性检验（ARMA建模前提）
def check_stationarity(series):
    """ADF检验判断平稳性"""
    adf_result = adfuller(series)
    print("\n平稳性检验（ADF）结果：")
    print(f"ADF统计量: {adf_result[0]:.2f}")
    print(f"p值: {adf_result[1]:.4f}")
    print(f"结论: {'平稳' if adf_result[1] < 0.05 else '非平稳，需差分'}")
    return adf_result[1] < 0.05  # 返回是否平稳的布尔值

is_stationary = check_stationarity(temp_series)


# 5. 步骤2：若非平稳则差分（这里数据已平稳，跳过差分）
# 若实际数据非平稳，需执行：stationary_series = temp_series.diff().dropna()
stationary_series = temp_series  # 当前数据平稳，直接使用


# 6. 步骤3：定阶（ACF/PACF图判断p和q）
plt.figure(figsize=(12, 8))

# ACF图（判断MA阶数q：看截尾位置）
plt.subplot(2, 1, 1)
plot_acf(stationary_series, lags=20, ax=plt.gca())  # 显示前20阶滞后
plt.title('ACF图（判断MA阶数q）', fontsize=12)

# PACF图（判断AR阶数p：看截尾位置）
plt.subplot(2, 1, 2)
plot_pacf(stationary_series, lags=20, ax=plt.gca(), method='ywm')  # 避免边界效应
plt.title('PACF图（判断AR阶数p）', fontsize=12)

plt.tight_layout()
plt.show()

# 根据图形观察定阶（示例结论：ACF拖尾，PACF在2阶截尾 → p=2, q=0）
p, q = 2, 0      # PACF在2阶截尾 p=2，q=0即不使用MA项


# 7. 步骤4：拟合ARMA模型（ARMA(p,q) = ARIMA(p,0,q)）
model = ARIMA(temp_series, order=(p, 0, q))  # order=(p, d, q)，d=0表示平稳序列
model_fit = model.fit()

# 输出模型参数（核心关注coef和P>|z|，P值越小参数越显著）
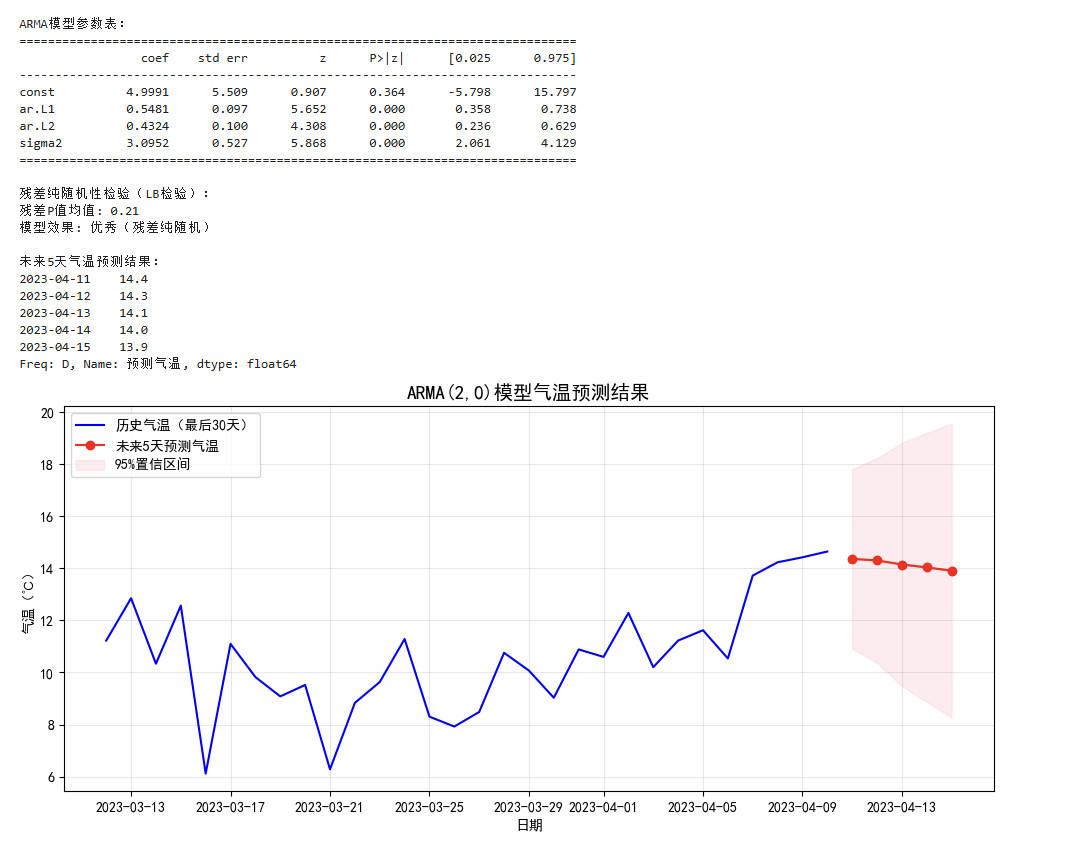
print("\nARMA模型参数表：")
print(model_fit.summary().tables[1])


# 8. 步骤5：残差检验（LB检验，判断模型是否捕捉所有规律）
residuals = model_fit.resid  # 获取残差（实际值-预测值）
lb_test = acorr_ljungbox(residuals, lags=10)  # 检验前10阶滞后
lb_pvalue_mean = lb_test['lb_pvalue'].mean()  # 平均p值

print("\n残差纯随机性检验（LB检验）：")
print(f"残差P值均值: {lb_pvalue_mean:.2f}")
print(f"模型效果: {'优秀（残差纯随机）' if lb_pvalue_mean >= 0.05 else '需优化（残差有规律）'}")


# 9. 步骤6：预测未来5天气温
forecast_days = 5  # 预测未来5天
forecast = model_fit.get_forecast(steps=forecast_days)  # 获取预测结果和置信区间
forecast_values = forecast.predicted_mean  # 预测值
conf_int = forecast.conf_int()  # 95%置信区间

# 生成预测日期索引
forecast_index = pd.date_range(start=temp_series.index[-1]+pd.Timedelta(days=1), periods=forecast_days)
forecast_series = pd.Series(forecast_values, index=forecast_index, name='预测气温')

# 打印预测结果
print("\n未来5天气温预测结果：")
print(forecast_series.round(1))  # 保留1位小数


# 10. 可视化预测结果（历史数据+预测值+置信区间）
plt.figure(figsize=(12, 5))
# 绘制历史数据
plt.plot(temp_series[-30:], color='blue', label='历史气温（最后30天）')  # 只显示最近30天
# 绘制预测值
plt.plot(forecast_series, color='red', marker='o', label='未来5天预测气温')
# 绘制置信区间（不确定性范围）
plt.fill_between(conf_int.index, conf_int.iloc[:,0], conf_int.iloc[:,1], color='pink', alpha=0.3, label='95%置信区间')

plt.title(f'ARMA({p},{q})模型气温预测结果', fontsize=14)
plt.xlabel('日期')
plt.ylabel('气温（℃）')
plt.legend()
plt.grid(alpha=0.3)
plt.show()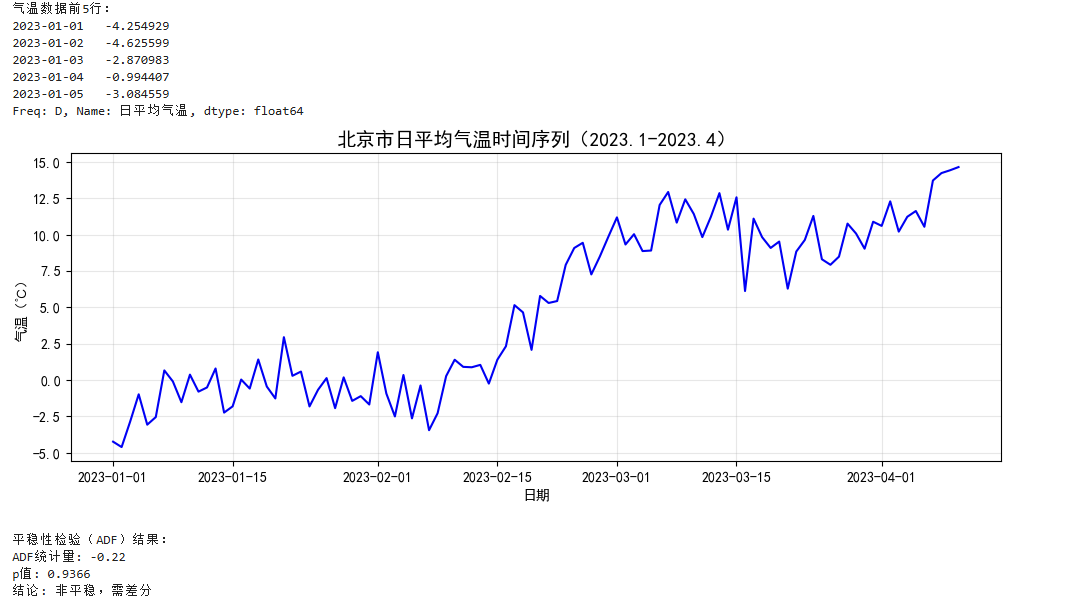

2.5 季节性差分自回归移动平均模型SARIMA

上节课学的 ARIMA 模型能解决 “有趋势的非平稳序列”（比如逐年增长的营收），但遇到 带季节性的序列就 “束手无策” 了—— 比如：

冰淇淋销量 ：每年夏季暴涨、冬季低迷（年度季节性）；
电商订单量 ：每月 11 日、12 日（促销日）激增（月度季节性）；
电力负荷： 每天早 8 点、晚 7 点（上下班高峰）飙升（日度季节性）。

简单说：SARIMA = ARIMA + 季节性差分 + 季节性 AR/MA 项，是处理季节性序列的 “专属神器”。

ARIMA和SARIMA的核心作用 👇

模型	解决的问题	奶茶店案例中的操作
ARMA	平稳序列（无趋势、无季节）	仅用于消除趋势和季节后的纯随机波动建模
ARIMA	非平稳序列（有趋势）	通过"1阶差分"消除长期增长趋势
SARIMA	季节性非平稳序列	通过"季节性差分（如7阶）"消除周期波动

ARMA：处理"平稳无周期"的数据（如每日心率波动）。
ARIMA：处理"有趋势但无周期"的数据（如个人月收入增长）。
SARIMA：处理"既有趋势又有周期"的数据（如奶茶店销量、空调销量）。

三者本质是"递进关系"，核心是通过差分（趋势差分、季节差分）让序列平稳，再用ARMA捕捉剩余规律。

数据仓库与数据挖掘-第12章节

1. 文本和时序数据挖掘

1. 文本数据挖掘概要

1. 文本挖掘是什么？

2. 文本挖掘的过程和任务

3. 文本挖掘的任务

2. 文本数据挖掘主要方法

4. 文本分析和挖掘的主要方法

4.1 词语分词

4.2 词性标注与停用词过滤

4.3 文本表征

4.3.1 词袋模型(Bag of Word) 一种“简单粗暴”的表示法

4.3.2 词频-逆文档频率（TF-IDF） ----- 给词语加上“重要性”权重

4.4 文本分类--给文本贴标签的“智能秘书”

4.5 文本聚类发现文本中的“自然群落”

4.6 文本可视化：让数据“自己说话”

3.时序数据挖掘

0.为什么要学习时序数据分析？

1. 时间序列和时间序列分析

2. 时间序列平稳性和随机性判定

2.1. 时间序列的平稳性”

2.2 时间序列纯随机性检验

2.3 自回归滑动平均ARMA模型

2.4 差分整合移动平均自回归ARIMA模型

2.5 季节性差分自回归移动平均模型SARIMA