数据仓库与数据挖掘

yange大约 20 分钟大数据学科数仓

聚类

1. 聚类分析概述

组合分类

定义

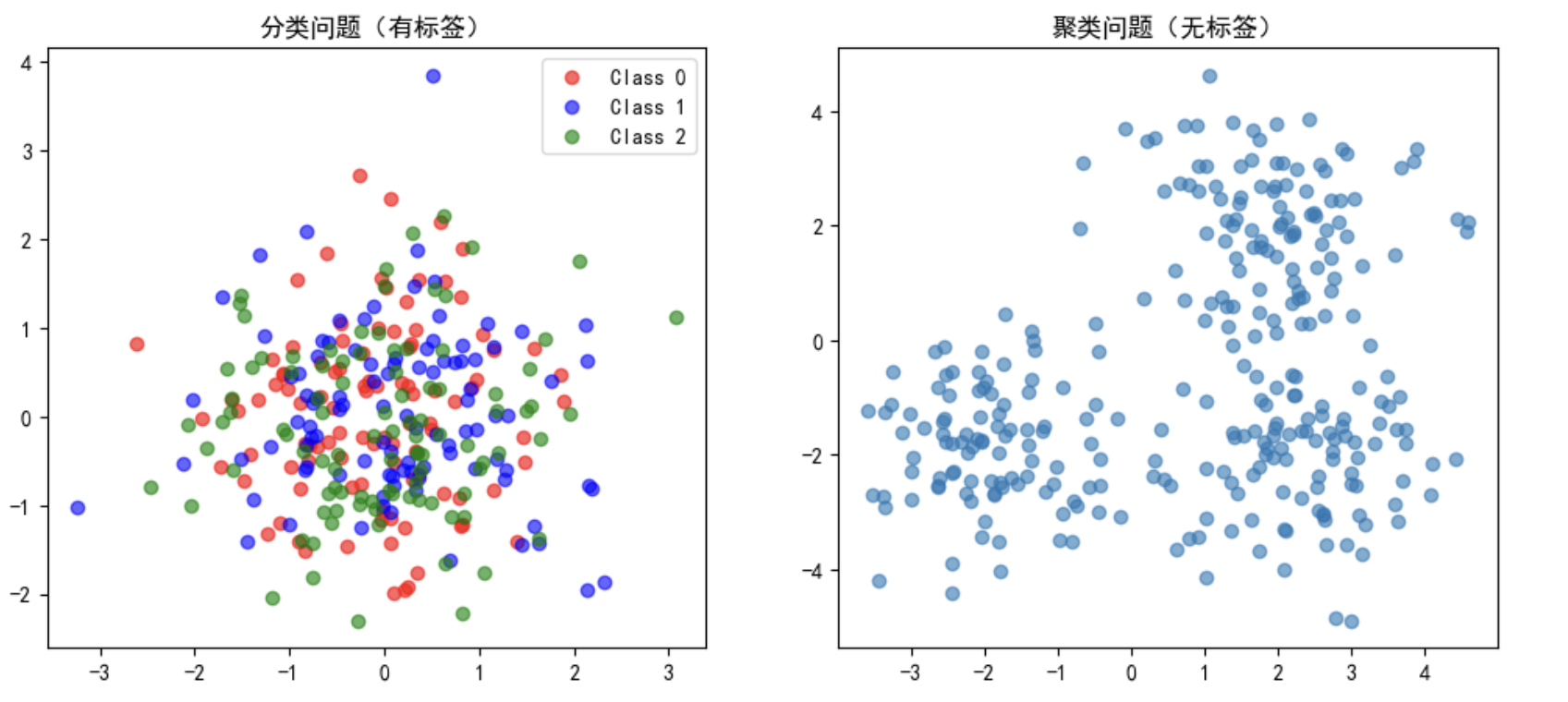
1. 什么是聚类？—— 从整理房间说起

生活中的聚类例子
想象你要整理一个混乱的房间：

书本放在书架上
衣服挂在衣柜里
文具收进笔筒
食品放进冰箱

这个过程就是聚类！你把相似的物品归为一类，让房间变得有序。

聚类是一种 无监督学习方法，目标是将数据分成不同的组（簇），使得：

同一簇内的数据点尽可能相似
不同簇之间的数据点尽可能不同

特征	分类	聚类
是否有标签	有标签（监督学习）	无标签（无监督学习）
目标	预测新数据的类别	发现数据的内在结构
例子	判断邮件是垃圾邮件还是正常邮件	将客户分成不同的群体

2. 聚类算法的分类

2.1 基于划分的方法

代表算法：K-Means
思想：将数据划分成K个簇，每个簇有一个中心点
特点：需要预先指定簇的数量K

2.2 基于层次的方法

代表算法：凝聚层次聚类，分裂层次聚类
思想：通过层层合并或分裂来构建树状结构
特点：不需要指定K值，结果呈现树状图

2.3 基于密度的方法

代表算法：DBSCAN
思想：根据数据点的密度来形成簇
特点：能发现任意形状的簇，对噪声不敏感

2.4 基于网格的方法

代表算法：STING, CLIQUE
思想：将数据空间划分为网格单元进行处理
特点：处理速度快，适合大数据集

2. K-Means聚类算法

组合分类

定义

1. K-Means算法的原理

K-Means原理：一个分组的游戏

游戏规则：

随机选择K个点作为初始中心点（质心）
将每个数据点分配给最近的中心点
重新计算每个簇的中心点（取平均值）
重复步骤2-3，直到中心点不再变化

K-Means的数学原理，目标函数（簇内平方和）：

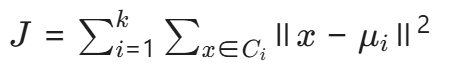
k：簇的数量; Ci：第i个簇; μi：第i个簇的中心点;x：数据点

1. **初始化簇中心**  
   随机选择( K )个样本作为初始簇中心

2. **分配样本到最近簇**  
   对每个样xi，计算与所有簇中心的距离，分配到距离最近的簇：  

3. **更新簇中心**  
   重新计算每个簇的中心为簇内样本的均值：  


4. **收敛判断**  
   重复步骤2和3，直到：  
   - 簇中心不再变化（或变化小于预设阈值）  
   - 达到最大迭代次数

2. K-Means的改进与变体

问题：原始K-Means对初始中心点敏感，可能陷入局部最优

解决方案：K-Means++

第一个中心点随机选择
后续中心点选择远离已选中心点的数据点
大大提高了算法的稳定性和收敛速度

3. 对比K-Means和K-Means++

案例代码：👇

# K-Means vs K-Means++ 比较
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 生成数据
X, y_true = make_blobs(n_samples=300, centers=5, cluster_std=0.60, random_state=42)
# 300个样本，4个簇，每个簇的标准差为0.6，随机种子为42

plt.figure(figsize=(15, 5))

# 原始K-Means（多次运行显示不稳定性）
plt.subplot(1, 3, 1)
for i in range(5):
    kmeans = KMeans(n_clusters=4, init='random', n_init=1, random_state=i) # 初始化1次，每次都选择不同的质心
    y_pred = kmeans.fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=y_pred, alpha=0.6)
plt.title('K-Means')



# K-Means++
plt.subplot(1, 3, 2)
kmeans_plus = KMeans(n_clusters=4, init='k-means++', n_init=10, random_state=42) # 初始化10次，每次都选择不同的质心
y_pred_plus = kmeans_plus.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred_plus, alpha=0.6)
plt.title('K-Means++\n')

# 真实分布
plt.subplot(1, 3, 3)
plt.scatter(X[:, 0], X[:, 1], c=y_true, alpha=0.6)
plt.title('真实分布')

plt.tight_layout()
plt.show()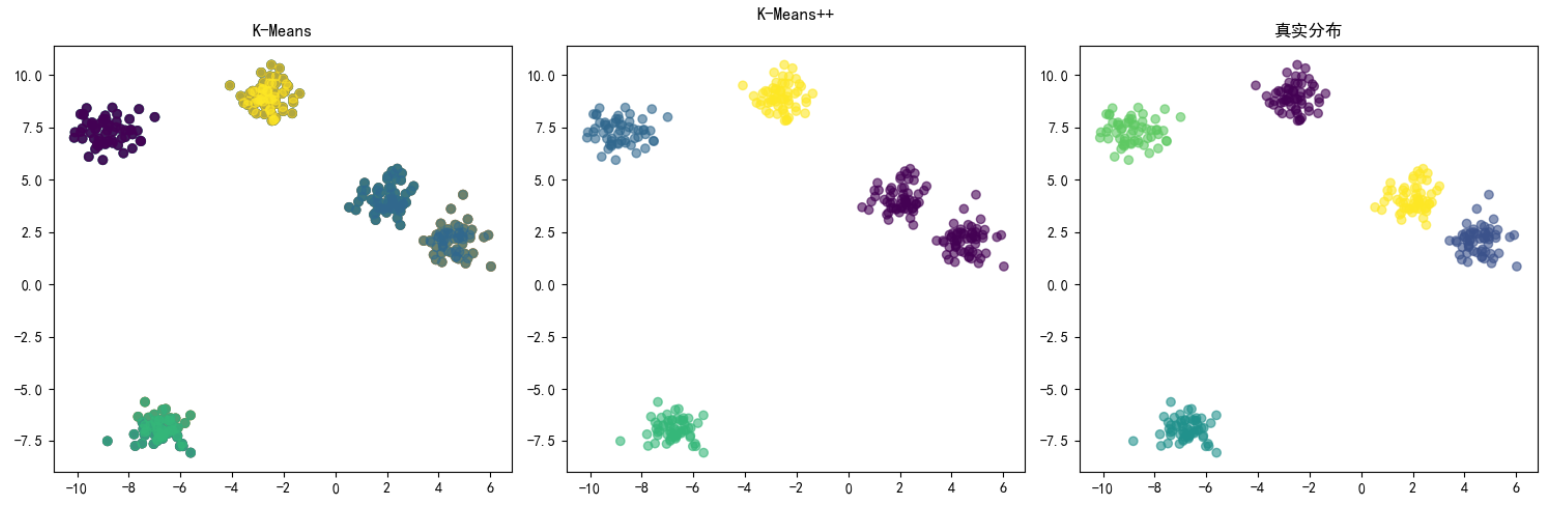

从上图我们发现K-Means聚类简洁高效，适合大规模数据挖掘，但是K-Means需要预先指定簇的数量，而类别数实现很难获取 .

3. 层级聚类

层级聚类

定义

前面我们学习了K-Means聚类算法，它是基于划分的方法，需要预先指定簇的数量。而层级聚类是一种基于层次的方法，不需要预先指定簇的数量，它通过连续合并或分裂来构建一个树状的聚类结构。

1.什么是层级聚类？—— 从家族关系说起

想象你要整理一个家族的族谱：

最底层 ：每个家庭成员是独立的个体
上一层 ：兄弟姐妹组成小家庭
再上一层 ：几个小家庭组成大家族
最顶层 ：整个家族汇聚在一起

这个过程就是层级聚类！

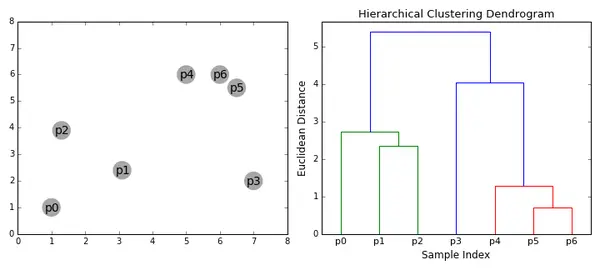
层级聚类通过连续 合并或分裂 来构建一个 树状的聚类结构，不需要预先指定簇的数量。

2. 为什么需要不同的距离度量？

想象你要判断两个班级学生的亲近程度，有不同方法：

看两个班最熟的两个人（单链接）
看两个班最陌生的两个人（全链接）
看两个班平均熟悉程度（平均链接）
看两个班长的关系（质心法）

2.1 最短距离法（单链接法）

📌 定义：
两个簇中最近的两个数据点之间的距离

📐 距离公式：

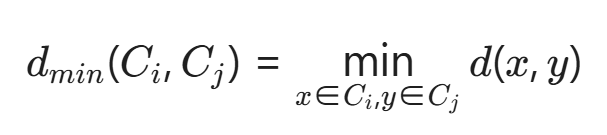
🎯 核心思想：
"只要两个簇中有任何两个点很接近，就认为这两个簇是亲近的"

📊 应用场景：
发现链状结构 ：适合识别非球形的、拉长的簇
异常检测 ：能够将离群点单独分离
形状复杂的簇 ：适用于簇形状不规则的情况

⚠️ 注意事项：
容易产生"链式效应"，可能把本不该在一起的簇连接起来

2.2 最长距离法（全链接法）

📌定义：
两个簇中最远的两个数据点之间的距离

📐 距离公式：

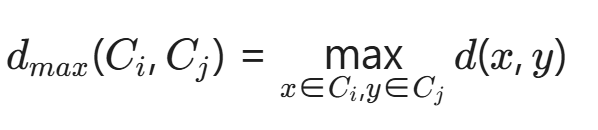
🎯 核心思想：
"必须两个簇中所有点都相对接近，才认为这两个簇是亲近的"

📊 应用场景：

紧凑球形簇：适合发现大小均匀的球形簇
质量要求高：当需要簇内点之间距离都很小时
噪声数据处理：对异常值比较敏感，能产生紧凑的簇

⚠️ 注意事项：
可能过度拆分数据，把本应在一起的簇分开

2.3 类平均法（平均链接法）

📌 定义：
两个簇中所有点对之间的平均距离

📐 距离公式：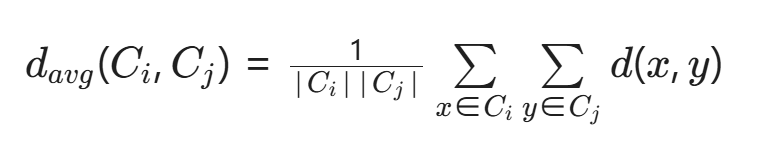

🎯 核心思想：
"看两个簇之间整体的平均亲近程度"

📊应用场景：
一般聚类分析：最常用、最平衡的方法
不知道数据特性时：作为默认选择
稳健性要求高：对噪声的敏感度介于最短和最远之间

⚠️ 注意事项：
计算量相对较大，但通常效果最好 👈 👈 👈

2.4 中心法（质心法）

📌定义：
两个簇的中心点（质心）之间的距离

📐 距离公式：

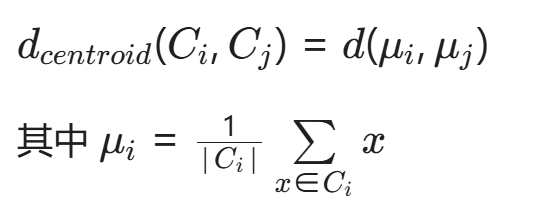
🎯 核心思想：
"看两个簇的代表点（中心）之间的距离"

📊 应用场景：

球形分布数据：当簇呈球形分布时效果最好
概念直观：适合需要容易解释的场景
计算效率：相对计算量较小

⚠️ 注意事项：
当簇大小差异很大时可能效果不佳

3. 分裂层次聚类（自顶向下）

🎯 基本思想：从整体开始，逐步分裂

🗺️ 生活比喻：国家行政区划

开始：整个中国作为一个整体
第一步：分成34个省级行政区
第二步：每个省分成多个地级市
第三步：每个市分成多个区县
最终：得到基层行政单位

📊 算法步骤：

初始状态：所有点在一个大簇中
↓
选择最需要分裂的簇
↓
将该簇分裂为两个子簇
↓
重复直到每个点独立或满足停止条件

4. 凝聚层次聚类（自底向上）

🎯 基本思想：从个体开始，逐步合并

📊 算法步骤:

初始状态：每个点都是一个簇
↓
找到距离最近的两个簇并合并
↓
更新距离矩阵
↓
重复直到所有点合并为一个簇

🏢 生活比喻：公司合并过程

开始：每个小公司独立运营
第一步：A公司和B公司合并
第二步：C公司和D公司合并
第三步：AB集团和CD集团合并
最终：形成一个大集团公司

凝聚法更常用:

实现简单：合并策略比分裂策略更容易实现
结果稳定：不容易受到随机性的影响
计算可行：虽然复杂度高，但对中小数据集可行

4. 基于密度的聚类

基于密度的聚类

定义

1. 从生活中的密度概念说起

生活中的密度现象：

人群聚集：商场里人群密集的地方形成"热点区域"
星星分布：宇宙中星星密集的地方形成"星系"
城市发展：人口密集的地方形成"城市中心"

K-Means和层次聚类有什么局限？

只能发现球形的簇
对噪声点敏感
无法发现任意形状的簇

2. 基于密度聚类的核心思想

🎯 **基本理念：**物以类聚，人以群分
密度聚类认为：

簇是数据空间中高密度区域
噪声存在于低密度区域
不同簇之间被低密度区域分隔

3. DBSCAN算法(最经典的密度聚类算法)

3.1 三个核心概念：

1. ε-邻域: 以点p为中心，半径为ε的圆形区域
2. 核心点: 如果点p的ε-邻域内至少包含MinPts个点（包括自己），则p为核心点
3. 密度直达: 点q在点p的ε-邻域内，且p是核心点,那么q从p密度直达

3.2 算法步骤

1. 标记所有点为未访问
2. 随机选择一个未访问点p
3. 如果p是核心点：
   - 创建新簇C
   - 将p及所有密度可达点加入C
4. 如果p是噪声点，标记为噪声
5. 重复直到所有点被访问

4. DBSCAN聚类算法实战：鸢尾花数据集分析

数据加载和探索

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
import pandas as pd

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

print("=== 简单DBSCAN鸢尾花聚类案例 ===\n")
# 加载数据
iris = load_iris()
X = iris.data  # 特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度
y = iris.target  # 真实类别：0-setosa, 1-versicolor, 2-virginica

print("数据基本信息：")
print(f"样本数: {X.shape[0]}, 特征数: {X.shape[1]}")
print(f"真实类别分布: Setosa-50, Versicolor-50, Virginica-50")

# 只看前两个特征方便可视化
X_simple = X[:, :2]  # 只用花萼长度和花萼宽度
print(f"\n使用前两个特征进行聚类: {iris.feature_names[:2]}")

结果：

=== 简单DBSCAN鸢尾花聚类案例 ===

数据基本信息：
样本数: 150, 特征数: 4
真实类别分布: Setosa-50, Versicolor-50, Virginica-50

使用前两个特征进行聚类: ['sepal length (cm)', 'sepal width (cm)']

数据标准化

# DBSCAN对数据尺度敏感，需要标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_simple)

print("标准化完成！")
print("原始数据范围:", f"花萼长度: {X_simple[:,0].min():.1f}-{X_simple[:,0].max():.1f}", 
      f"花萼宽度: {X_simple[:,1].min():.1f}-{X_simple[:,1].max():.1f}")
print("标准化后范围:", f"花萼长度: {X_scaled[:,0].min():.1f}-{X_scaled[:,0].max():.1f}", 
      f"花萼宽度: {X_scaled[:,1].min():.1f}-{X_scaled[:,1].max():.1f}")

结果：

标准化完成！
原始数据范围: 花萼长度: 4.3-7.9 花萼宽度: 2.0-4.4
标准化后范围: 花萼长度: -1.9-2.5 花萼宽度: -2.4-3.1

可视化原始数据

# 绘制原始数据分布
plt.figure(figsize=(15, 5))

plt.subplot(1, 3, 1)
colors = ['red', 'blue', 'green']
for i in range(3):
    plt.scatter(X_simple[y == i, 0], X_simple[y == i, 1], 
                c=colors[i], label=iris.target_names[i], alpha=0.7)
plt.xlabel('花萼长度')
plt.ylabel('花萼宽度')
plt.title('原始数据 - 真实分类')
plt.legend()
plt.grid(True, alpha=0.3)

# 绘制标准化后的数据
plt.subplot(1, 3, 2)
for i in range(3):
    plt.scatter(X_scaled[y == i, 0], X_scaled[y == i, 1], 
                c=colors[i], label=iris.target_names[i], alpha=0.7)
plt.xlabel('标准化花萼长度')
plt.ylabel('标准化花萼宽度')
plt.title('标准化后数据')
plt.legend()
plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

print("\n观察数据分布：")
print("• Setosa类（红色）明显与其他两类分开")
print("• Versicolor和Virginica有部分重叠")
print("• 这正是DBSCAN可以发挥优势的地方！")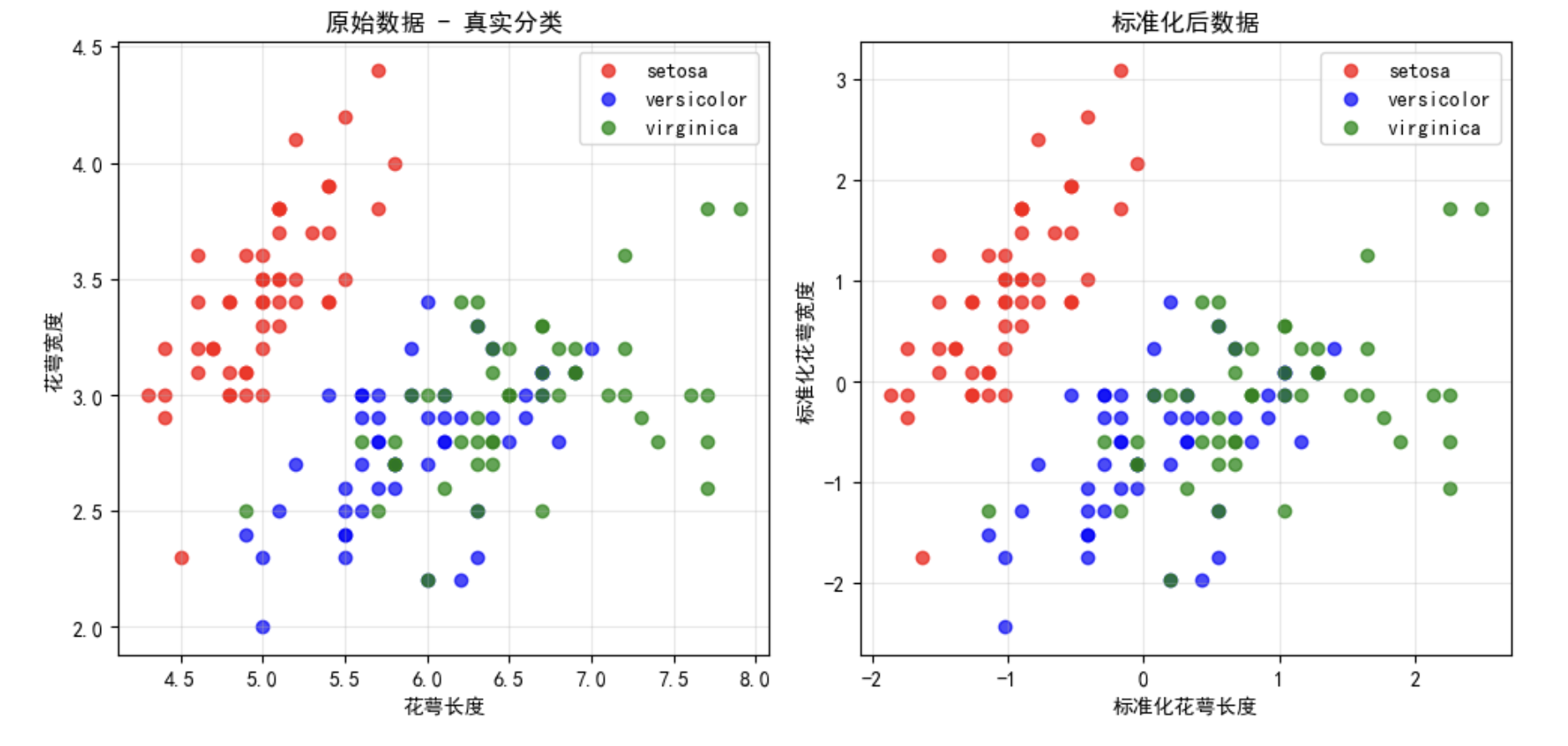

观察数据分布：

Setosa类（红色）明显与其他两类分开
Versicolor和Virginica有部分重叠
这正是DBSCAN可以发挥优势的地方！

运行DBSCAN聚类

# 使用DBSCAN进行聚类
print("\n开始DBSCAN聚类...")

# 设置参数：epsilon=0.5, min_samples=5
dbscan = DBSCAN(eps=0.5, min_samples=5)
labels = dbscan.fit_predict(X_scaled)

# 分析聚类结果
n_clusters = len(set(labels)) - (1 if -1 in labels else 0)
n_noise = list(labels).count(-1)

print("聚类结果：")
print(f"识别出的簇数量: {n_clusters}")
print(f"噪声点数量: {n_noise}")
print(f"聚类标签: {set(labels)}")

# 显示每个簇的样本数
for i in range(n_clusters):
    cluster_size = list(labels).count(i)
    print(f"簇{i}的样本数: {cluster_size}")

结果：

开始DBSCAN聚类...
聚类结果：
识别出的簇数量: 1
噪声点数量: 8
聚类标签: {np.int64(0), np.int64(-1)}
簇0的样本数: 142

可视化聚类结果

# 绘制聚类结果
plt.figure(figsize=(15, 5))

# DBSCAN聚类结果
plt.subplot(1, 3, 1)
# 为每个簇分配颜色
cluster_colors = ['blue', 'green', 'orange', 'purple', 'brown']
noise_color = 'red'

for cluster_id in range(n_clusters):
    mask = labels == cluster_id
    plt.scatter(X_simple[mask, 0], X_simple[mask, 1], 
                c=cluster_colors[cluster_id], label=f'簇{cluster_id}', alpha=0.7)

# 标记噪声点
if n_noise > 0:
    noise_mask = labels == -1
    plt.scatter(X_simple[noise_mask, 0], X_simple[noise_mask, 1], 
                c=noise_color, label='噪声点', marker='x', s=100)

plt.xlabel('花萼长度')
plt.ylabel('花萼宽度')
plt.title('DBSCAN聚类结果')
plt.legend()
plt.grid(True, alpha=0.3)

# 与真实分类对比
plt.subplot(1, 3, 2)
for i in range(3):
    plt.scatter(X_simple[y == i, 0], X_simple[y == i, 1], 
                c=colors[i], label=iris.target_names[i], alpha=0.7)
plt.xlabel('花萼长度')
plt.ylabel('花萼宽度')
plt.title('真实分类')
plt.legend()
plt.grid(True, alpha=0.3)

# 并排对比
plt.subplot(1, 3, 3)
# 用形状区分DBSCAN结果，用颜色区分真实类别
markers = ['o', 's', '^', 'D', 'v']  # 不同形状表示不同簇

for cluster_id in range(n_clusters):
    mask = labels == cluster_id
    for true_class in range(3):  # 在每个簇内按真实类别着色
        class_mask = mask & (y == true_class)
        if np.sum(class_mask) > 0:
            plt.scatter(X_simple[class_mask, 0], X_simple[class_mask, 1], 
                       c=colors[true_class], marker=markers[cluster_id],
                       label=f'簇{cluster_id}-{iris.target_names[true_class]}',
                       alpha=0.7)

if n_noise > 0:
    noise_mask = labels == -1
    plt.scatter(X_simple[noise_mask, 0], X_simple[noise_mask, 1], 
                c='black', marker='x', s=100, label='噪声点')

plt.xlabel('花萼长度')
plt.ylabel('花萼宽度')
plt.title('DBSCAN结果 vs 真实类别')
plt.legend()
plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()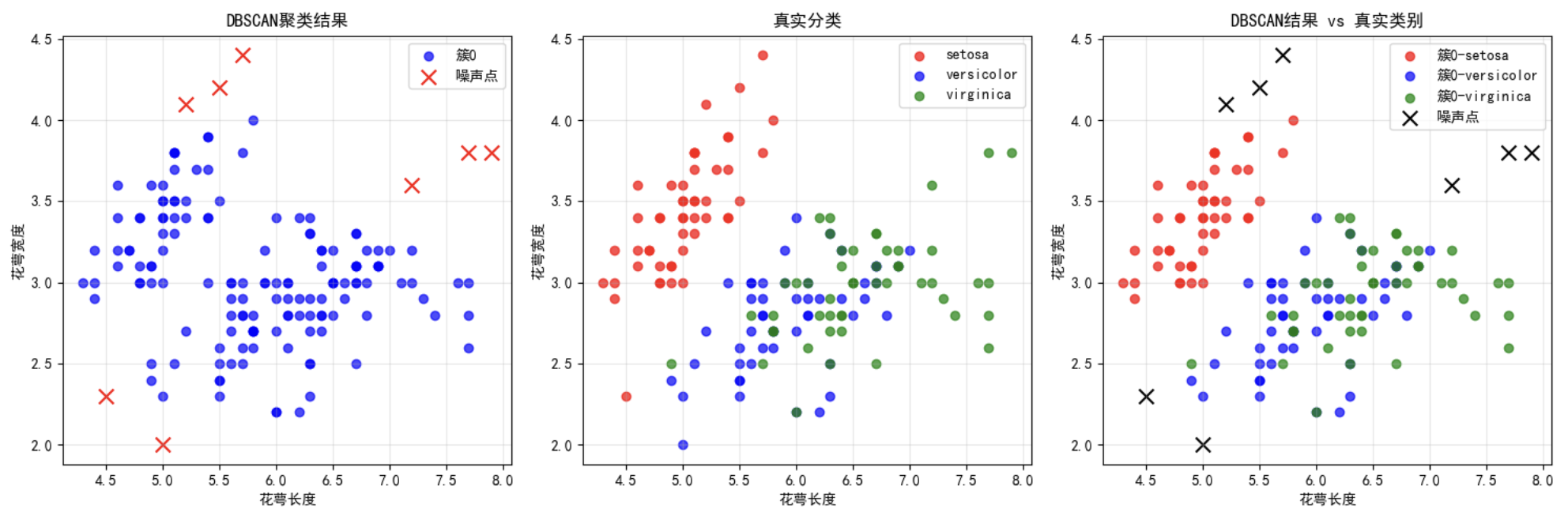

分析聚类效果

# 简单分析聚类质量
print("\n=== 聚类效果分析 ===")

# 检查每个簇的真实类别构成
for cluster_id in range(n_clusters):
    mask = labels == cluster_id
    cluster_true_labels = y[mask]
    print(f"\n簇{cluster_id} ({len(cluster_true_labels)}个样本):")
    
    for true_class in range(3):
        count = np.sum(cluster_true_labels == true_class)
        if count > 0:
            percentage = count / len(cluster_true_labels) * 100
            print(f"  {iris.target_names[true_class]}: {count}个 ({percentage:.1f}%)")

# 分析噪声点
if n_noise > 0:
    noise_mask = labels == -1
    noise_true_labels = y[noise_mask]
    print(f"\n噪声点分析 ({n_noise}个):")
    
    for true_class in range(3):
        count = np.sum(noise_true_labels == true_class)
        if count > 0:
            percentage = count / n_noise * 100
            print(f"  {iris.target_names[true_class]}: {count}个 ({percentage:.1f}%)")

结果：

=== 聚类效果分析 ===

簇0 (142个样本):
  setosa: 46个 (32.4%)
  versicolor: 49个 (34.5%)
  virginica: 47个 (33.1%)

噪声点分析 (8个):
  setosa: 4个 (50.0%)
  versicolor: 1个 (12.5%)
  virginica: 3个 (37.5%)

尝试不同参数

# 尝试不同的参数组合
print("\n=== 尝试不同参数的效果 ===")

param_combinations = [
    (0.3, 5),  # ε较小
    (0.5, 5),  # 适中
    (0.8, 5),  # ε较大
    (0.5, 3),  # MinPts较小
    (0.5, 10)  # MinPts较大
]

plt.figure(figsize=(20, 4))

for i, (eps, min_samples) in enumerate(param_combinations):
    dbscan_test = DBSCAN(eps=eps, min_samples=min_samples)
    labels_test = dbscan_test.fit_predict(X_scaled)
    
    n_clusters_test = len(set(labels_test)) - (1 if -1 in labels_test else 0)
    n_noise_test = list(labels_test).count(-1)
    
    plt.subplot(1, 5, i+1)
    
    # 绘制聚类结果
    for cluster_id in range(n_clusters_test):
        mask = labels_test == cluster_id
        plt.scatter(X_simple[mask, 0], X_simple[mask, 1], 
                   c=cluster_colors[cluster_id], alpha=0.7)
    
    if n_noise_test > 0:
        noise_mask = labels_test == -1
        plt.scatter(X_simple[noise_mask, 0], X_simple[noise_mask, 1], 
                   c=noise_color, marker='x', s=80)
    
    plt.xlabel('花萼长度')
    plt.ylabel('花萼宽度')
    plt.title(f'ε={eps}, MinPts={min_samples}\n簇数:{n_clusters_test}, 噪声:{n_noise_test}')
    plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

print("参数影响总结：")
print("• ε越小：簇越多，噪声点越多")
print("• ε越大：簇越少，噪声点越少") 
print("• MinPts越小：更容易形成簇")
print("• MinPts越大：要求更严格，噪声点更多")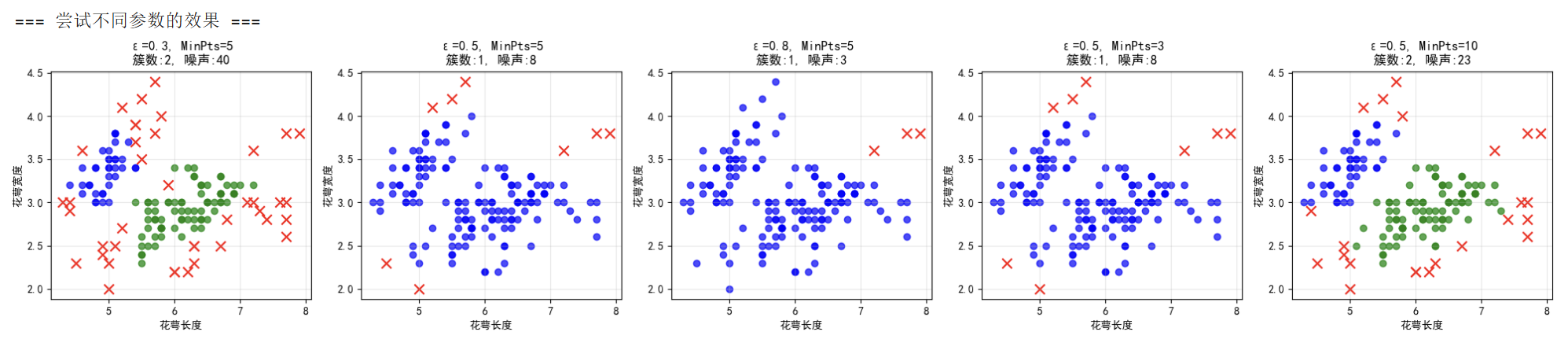

运行结果说明

✅ DBSCAN的优势：

自动发现簇数量，不用预先设定
能识别噪声点（不属于任何簇的数据）
可以发现任意形状的簇

📊 在本案例中的表现：
• 成功将Setosa类与其他两类分开
• 自动识别出1个自然簇
• 发现8个边界上的噪声点

💡 核心参数说明：
• ε (eps): 邻域半径，决定两个点是否算邻居
• MinPts: 最小邻居数，决定一个点是否算核心点

🎯 适用场景：
• 数据中有自然聚集，但不知道具体有几个簇
• 需要找出异常值或噪声点
• 簇的形状可能不是标准的圆形
:::

5.其他聚类方法

前言

定义

1. STING聚类：网格化的智能聚类

🎯 **基本思想：**用网格划分数据空间，分层统计

生活比喻：人口普查网格化管理

将城市划分为不同的网格区域
每个网格统计人口密度、年龄分布等
从细网格逐步汇总到粗网格

📊 STING 算法流程：：

1. 将数据空间划分为层次化网格
2. 从底层开始计算每个网格的统计信息
3. 自顶向下查询：从粗网格到细网格
4. 只访问相关的网格，避免全数据扫描

💼 应用场景：智慧城市热点分析

案例：共享单车投放优化

# 使用STING聚类分析骑行热点
层级1网格：100m×100m，统计每小时的骑行量
层级2网格：500m×500m，识别区域热点模式  
层级3网格：1km×1km，制定宏观投放策略

价值：快速定位热点区域，优化车辆调度

2. 概念聚类：基于概念的智能分组s

🎯 基本思想：不仅看特征相似，更看概念相关

生活比喻：图书馆图书分类

不是按书本大小颜色分类
而是按"科学"、"文学"、"历史"等概念分类
考虑内容的相关性和逻辑关系

💼 应用场景：电商商品智能分类

案例：电子产品概念聚类

传统聚类结果：
簇1：{iPhone12, iPad Pro, MacBook} # 按品牌价格聚集
簇2：{三星手机, 华为平板} # 按安卓系统聚集

概念聚类结果：
概念簇1："苹果生态系统" 
    - 描述：设备间无缝协作，iCloud同步
    - 成员：iPhone, iPad, Mac, Watch
    
概念簇2："商务办公设备"
    - 描述：高效办公，长续航，多任务处理  
    - 成员：Surface, ThinkPad, 华为MatePad

3. 模糊聚类：打破"非此即彼"的界限

🎯 基本思想：一个点可以属于多个簇，有隶属度
生活比喻：人的多重身份

一个人可以是：程序员(0.7)+音乐家(0.2)+摄影师(0.1)
不是"要么是程序员，要么不是"
而是在不同身份间有不同程度的归属

📊 FCM原理

1. 先搞懂 “模糊”：不是非黑即白，而是 “有点像”
比如给 3 种水果（苹果、香蕉、橙子）聚类，K-Means 会说 “这个水果 100% 是苹果类”；但 FCM 会说 “这个水果 60% 像苹果、30% 像橙子、10% 像香蕉”—— 这里的百分比就是 “隶属度”，每个样本对所有簇都有一个隶属度，加起来刚好是 100%。

2. 目标很直接：让 “像的样本” 尽量凑一起
FCM 最终想实现的是：
每个簇里的样本，对这个簇的 “隶属度” 都要高（比如苹果簇里的样本，大多 “80% 以上像苹果”）；

样本到自己 “主要隶属” 的簇中心，距离要近（比如 “80% 像苹果” 的样本，离苹果簇中心要近）。

就像让一群人找朋友，尽量让 “觉得彼此像朋友” 的人站在同一圈里。

3. 怎么做：先猜再调，直到满意

FCM 的过程类似 “试错优化”，分两步循环：

先给每个样本 “打分”：假设先随便定几个簇中心（比如先挑 3 个样本当临时中心），然后给每个样本算对每个中心的 “隶属度”（比如 A 样本对中心 1 打 80 分、中心 2 打 15 分、中心 3 打 5 分）。
再调整中心位置：根据第一步的 “打分”，把每个簇的中心挪到 “该簇所有样本的加权中间”（比如苹果簇中心，会往 “打高分的苹果样本” 那边挪）。
反复来几遍：重新按新中心给样本打分，再挪中心，直到中心位置基本不动、每个样本的隶属度也稳定了，就结束。

💼 应用场景：客户价值细分

案例：银行客户分层
硬聚类结果：
客户A：VIP客户（100%归属）
客户B：普通客户（100%归属）

模糊聚类结果：
客户A：VIP(0.8) + 潜在VIP(0.2)
客户B：普通(0.6) + 潜在流失(0.4)

业务价值：更精细的客户管理策略

4. FCM聚类算法案例

安装skfuzzy

pip install scikit-fuzzy


import numpy as np
import matplotlib.pyplot as plt
from skfuzzy.cluster import cmeans
from sklearn.datasets import load_iris

# 加载Iris数据集
iris = load_iris()
x = iris.data
shape = x.shape
colo = ['b', 'g', 'r', 'c', 'm']
EPC = []  # 用于存储各聚类数下的模糊划分系数（FPC）

# 尝试聚类数k从2到5
for k in range(2, 5):
    # 执行FCM聚类，m为模糊指数（默认2），error为收敛阈值，maxiter为最大迭代次数
    center, u,u0, d, jm, p, fpc = cmeans(x.T, m=2, c=k, error=0.5, maxiter=1000)
    EPC.append(fpc)
    # 确定每个样本的聚类标签（取隶属度最大的类别）
    label = np.argmax(u0, axis=0)
    
    # 可视化聚类结果（以前两个特征为例）
    plt.figure(figsize=(8, 6))
    for i in range(shape[0]):
        plt.scatter(x[i, 0], x[i, 1], color=colo[label[i]], s=50, alpha=0.8)
    plt.scatter(center[:, 0], center[:, 1], color='k', marker='*', s=200, label='聚类中心')
    plt.title(f'FCM聚类（k={k}，FPC={fpc:.3f}）')
    plt.xlabel(iris.feature_names[0])
    plt.ylabel(iris.feature_names[1])
    plt.legend()
    plt.show()

# 输出各聚类数对应的FPC
print("不同聚类数的模糊划分系数（FPC）：", EPC)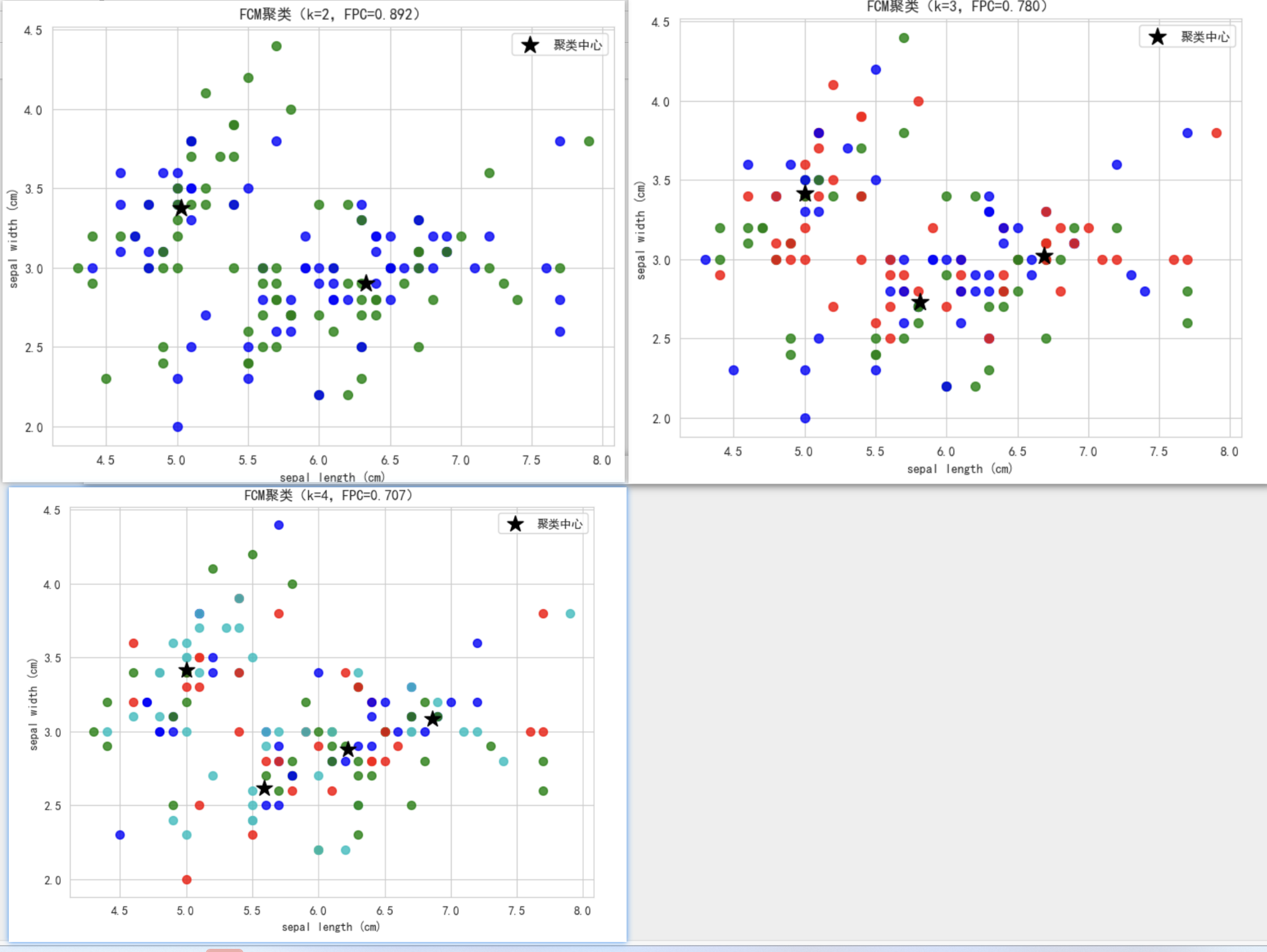

说明
聚类核心：cmeans函数实现 FCM 聚类，参数x.T是因为函数要求输入为 “特征数 × 样本数” 的矩阵；m=2是模糊指数的常用值；c=k是聚类数；error和maxiter控制收敛逻辑。
结果评估：fpc（模糊划分系数）越接近 1，聚类效果越好，可通过它选择最优聚类数。
可视化：以数据集前两个特征（花萼(sepal)长度、花萼宽度）绘制散点图，不同颜色代表不同聚类，黑色星号代表聚类中心，直观展示聚类分布。’

5.🎯实用建议：

数据量大且空间分布 → STING
需要业务解释性 → 概念聚类
类别有重叠边界 → 模糊聚类/FCM
一般情况 → 从K-Means开始尝试

数据仓库与数据挖掘

聚类

1. 聚类分析概述

1. 什么是聚类？—— 从整理房间说起

2. 聚类算法的分类

2. K-Means聚类算法

1. K-Means算法的原理

2. K-Means的改进与变体

3. 对比K-Means和K-Means++

3. 层级聚类

1. 什么是层级聚类？—— 从家族关系说起

1.什么是层级聚类？—— 从家族关系说起

2. 为什么需要不同的距离度量？

2.1 最短距离法（单链接法）

2.2 最长距离法（全链接法）

2.3 类平均法（平均链接法）

2.4 中心法（质心法）

3. 分裂层次聚类（自顶向下）

4. 凝聚层次聚类（自底向上）

5. 案例代码

4. 基于密度的聚类

1. 从生活中的密度概念说起

2. 基于密度聚类的核心思想

3. DBSCAN算法(最经典的密度聚类算法)

3.1 三个核心概念：

3.2 算法步骤

4. DBSCAN聚类算法实战：鸢尾花数据集分析

5.其他聚类方法

1. STING聚类：网格化的智能聚类

2. 概念聚类：基于概念的智能分组s

3. 模糊聚类：打破"非此即彼"的界限

4. FCM聚类算法案例

5.🎯实用建议：