数据仓库与数据挖掘
1.分类概述
分类概述
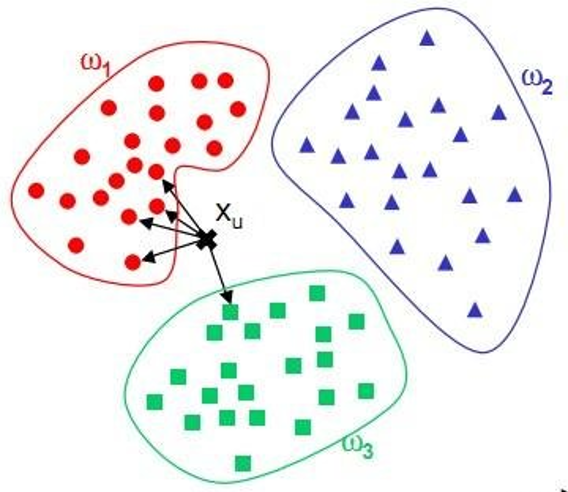
分类分析是指在已知研究对象已经分为若干类的情况下,确定新的对象属于哪一类。
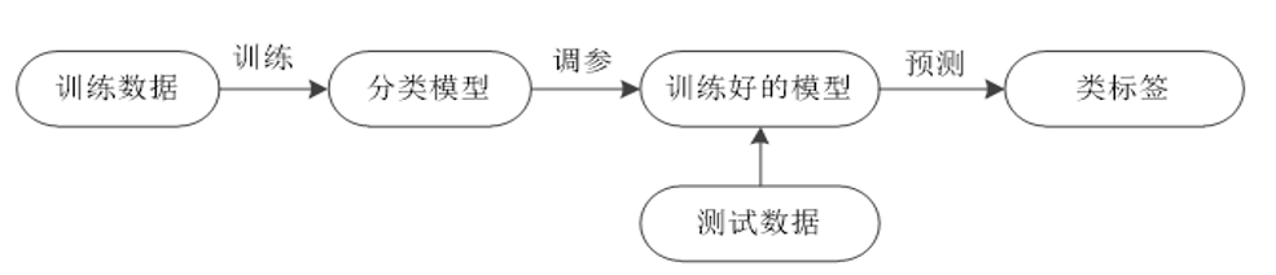
分类是一种重要的数据分析形式。数据分类也称为监督学习 ,包括学习阶段(构建分类模型)和分类阶段(使用模型预测给定数据的类标号)两个阶段。数据分类方法主要有:
- 决策树归纳
- 贝叶斯分类。
- K-近邻分类
- 支持向量机SVM等方法。
2.分类决策树归纳
分类概述
1.认识决策树
决策树思想的来源,非常朴素。程序设计中的条件分支结构就是 if-else结构,最早的决策树就是利用这类结构分割数据的一种分类学习方法。决策树算法简单直观,容易解释,而且在实际应用中具有其他算法难以比肩的速度优势。
决策树基本上就是把我们以前的经验总结出来,如下图中的场景,如果去相亲,一般会根据“年龄”、“长相”、“身高”、“收入”这几个条件来判断,最后得到结果:去?还是不去?
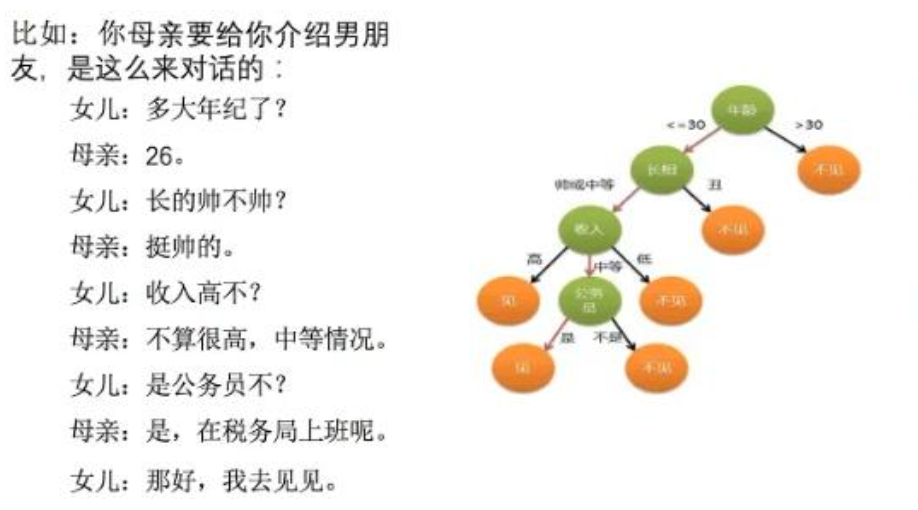
如何高效的进行决策?即:确定 特征的先后顺序。
上图就是一棵典型的决策树。我们在做决策树的时候,会经历两个阶段:构造和剪枝 。
1.1 构造
所谓构造 ,就是生成一棵完整的决策树。简单来说,构造的过程就是选择什么属性作为节点的过程,那么在构造过程中,会存在三种节点:
根节点 :就是树的最顶端,最开始的那个节点;
内部节点 :就是树中间的那些节点;
叶节点 :就是树最底部的节点,也就是决策结果。
节点之间存在父子关系。比如根节点会有子节点,子节点会有子子节点,但是到了叶节点就停止了,叶节点不存在子节点。
那么在构造过程中,你要解决三个重要的问题:选择哪个属性作为根节点?选择哪些属性作为子节点?什么时候停止并得到目标状态,即叶节点?
1.2 剪枝
决策树构造出来之后是不是就万事大吉了呢?也不尽然,我们可能还需要对决策树进行剪枝。
剪枝就是给决策树瘦身 ,这一步想实现的目标就是,不需要太多的判断,同样可以得到不错的结果。之所以这么做,是为了防止过拟合 (Overfitting)现象的发生。
过拟合:一个假设在训练数据上能够获得比其他假设更好的拟合,但是在测试数据集上,却不能很好的拟合数据,此时认为这个假设出现过拟合现象。(模型过于复杂), 如下图的1
欠拟合:一个假设在训练数据上不能获得更好的拟合,并且在测试数据集上,也不能很好的拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单),如下图3
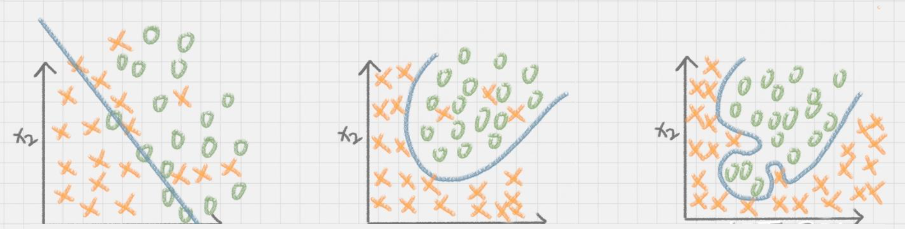
如果决策树选择的属性过多,构造出来的决策树一定能够“完美”地把训练集中的样本分类,但是这样就会把训练集中一些数据的特点当成所有数据的特点,但这个特点不一定是全部数据的特点,这就使得这个决策树在真实的数据分类中出现错误,也就是模型的“泛化能力”差。(就是举一反三的能力)
对决策树进行剪枝,一般来说,剪枝可以分为预剪枝(Pre-Pruning) 和 后剪枝(Post-Pruning)
其中 “后剪枝”中的“代价复杂度剪枝” 是 CART 最经典、最常用的剪枝方法(也是 sklearn 中默认实现的方法)。
预剪枝(“长到一半就停”):思想:在树的生长过程中,提前设定“停止条件”,一旦满足条件就不再分裂(避免树长得太深),工程实现简单,但容易过拟合(“过早停止”)。
后剪枝(“先长到最大,再剪枝”):思想:先让树“自由生长”到最复杂(过拟合状态),再从“叶子节点向上”逐步剪掉“无用的分支”,保留泛化能力最好的子树。理论上更优,但工程实现复杂。
实际运用:通常 “预剪枝+后剪枝结合”(先用预剪枝限制树的最大深度,再用 CCP 精细剪枝),兼顾效率和效果。
在 sklearn 的 DecisionTreeClassifier 和 DecisionTreeRegressor 中,默认开启后剪枝(CCP),并通过 ccp_alpha 参数控制(默认 ccp_alpha=0,可手动设置 ccp_alpha>0 启用剪枝)。
2. 决策树的构建原理
为了更好理解决策树,具体怎么分类的,我们通过如下的一个例子;
问题:某机构希望通过一个人的若干特征,判断它是否能够偿还债务。
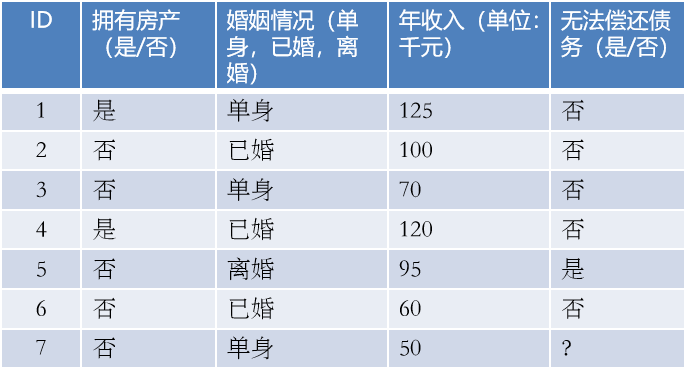
我应该借钱吗? 如何对这些客户进行分类预测?你是如何去划分?
那么,有可能你是这么划分的:
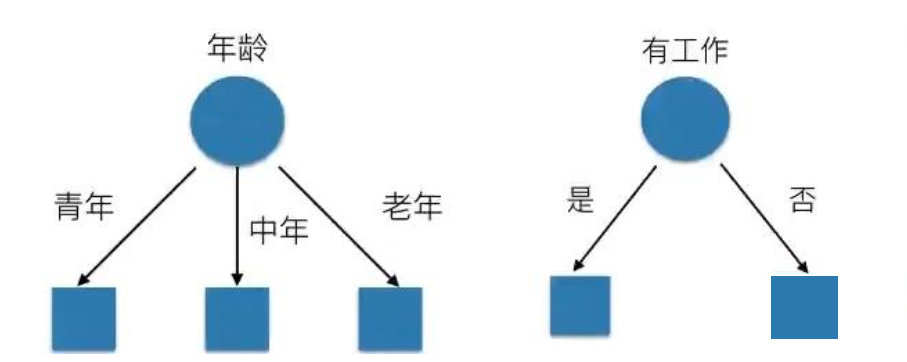
可能还有其他的划分方式,但是,我们怎么知道,这些特征哪个更好的放在最上面呢?
此时,再回顾一下决策树的构造原理,在决策过程中有三个重要的问题:将哪个属性作为根节点?选择哪些属性作为后继节点?什么时候停止并得到目标值?
显然将哪个属性(年龄、工作、房子、信贷)作为根节点是个关键问题,在这里我们先介绍两个指标:纯度和信息熵。
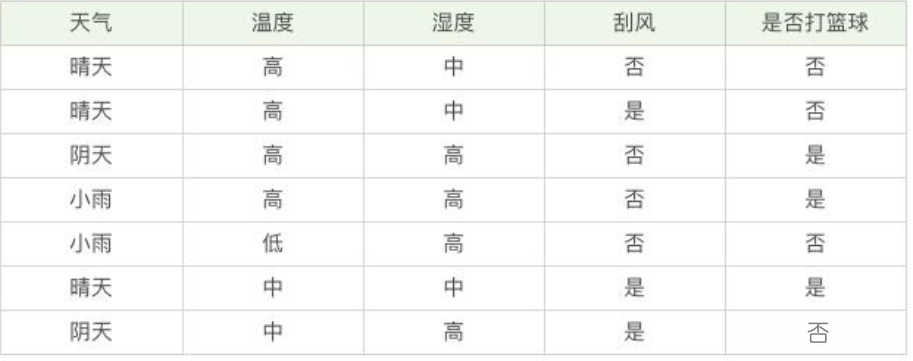
在这里举个例子,假设有 3 个集合:
集合 1:6 次都去打篮球;
集合 2:4 次去打篮球,2 次不去打篮球;
集合 3:3 次去打篮球,3 次不去打篮球。
1. 纯度
决策树的构造过程理解成为寻找纯净划分的过程。数学上,我们可以用纯度来表示,纯度换一种方式来解释就是让目标变量的分歧最小。
按照纯度指标来说,集合 1> 集合 2> 集合 3。 因为集合 1 的分歧最小,集合 3 的分歧最大。
2. 信息熵
信息熵(entropy)的概念,它表示了信息的不确定度。
在信息论中,随机离散事件出现的概率存在着不确定性。为了衡量这种信息的不确定性,信息学之父香农引入了信息熵的概念,并给出了计算信息熵的数学公式:👇
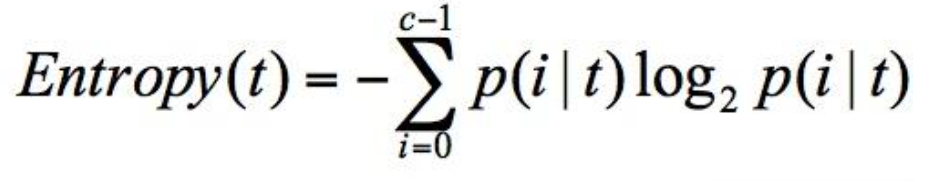
p(i|t) 代表了节点 t 为分类 i 的概率,其中 log2 为取以 2 为底的对数。这里我们不是来介绍公式的,而是说存在一种度量,它能帮我们反映出来这个信息的不确定度。当不确定性越大时,它所包含的信息量也就越大,信息熵也就越高。
还是用上面的例子,具体阐述一下信息熵的计算方式。假设有 2 个集合
集合1: 5 次去打篮球,1 次不去打篮球;
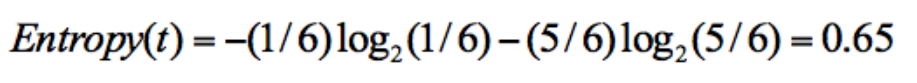
集合 2:3 次去打篮球,3 次不去打篮球;
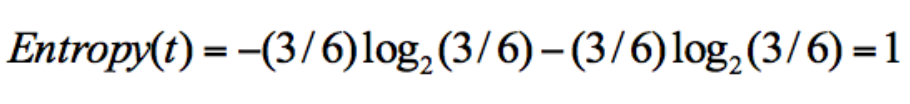
从上面的计算结果中可以看出,信息熵越大,纯度越低。当集合中的所有样本均匀混合时,信息熵最大,纯度最低。
3. ID3算法
ID3算法
3. ID3算法
ID3算法是决策树系列中的经典算法之一,包含了决策树作为机器学习算法的主要思想。但ID3算法在实际应用中有诸多不足,因此之后提出了大量的改进算法,如C4.5算法和CART算法。构造决策树的核心问题是在每一步如何选择恰当的属性对样本做拆分。ID3算法使用信息增益作为属性选择度量,C4.5使用增益率进行属性选择度量,CART算法则使用基尼指数.
3.1 我们为什么需要信息增益?
想象一下,你要根据历史数据构建一个模型,来预测客户是否会购买一款新产品。你有许多客户特征(属性),如“年龄”、“职业”、“是否收到营销邮件”等。
核心问题: 在构建决策树模型时,我们应该先根据哪个属性来提问(分裂节点)?是先问“年龄”还是先问“是否收到营销邮件”?
答案: 我们应该选择那个能让数据变得更“纯”、不确定性下降最多的属性。信息增益(Information Gain) 就是用来量化这个“不确定性下降” 程度的指标。信息增益越大的属性,意味着用它来分裂所获得的“信息”越多,效果越好,因此应该优先选择它作为决策树的根节点或分支节点。
ID3 算法计算的是信息增益,信息增益指的就是划分可以带来纯度的提高,信息熵的下降。
计算公式,是父亲节点的信息熵减去所有子节点的信息熵。在计算的过程中,我们会计算每个子节点的归一化信息熵,即按照每个子节点在父节点中出现的概率,来计算这些子节点的信息熵。所以信息增益的公式可以表示为:
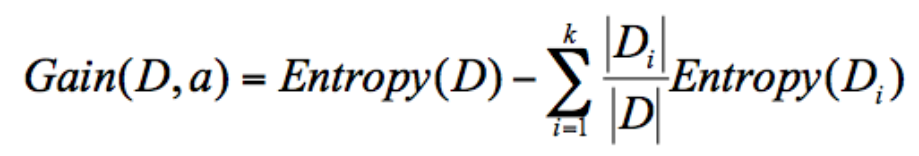
信息增益 = 父亲节点的熵 - 儿子们节点的熵的加权平均。信息增益越大,说明这个属性选择的越好。
3.2 ID3算法核心思想
一句话概括ID3: 自顶向下,贪心迭代,选择信息增益最大的属性作为节点来构建决策树。
我们来拆解这句话:👇
- 自顶向下:从树的根节点开始,一步步向下生长。
- 贪心迭代:在当前时刻、当前的数据子集上,只选择当下看来最好的属性(即信息增益最大的属性),而不考虑长远影响。这种“只看眼前最优”的策略就叫“贪心”。
- 信息增益最大:这就是我们上节课学的内容,是选择属性的唯一标准!
接下来通过下面这个案例来理解ID3算法的核心思想: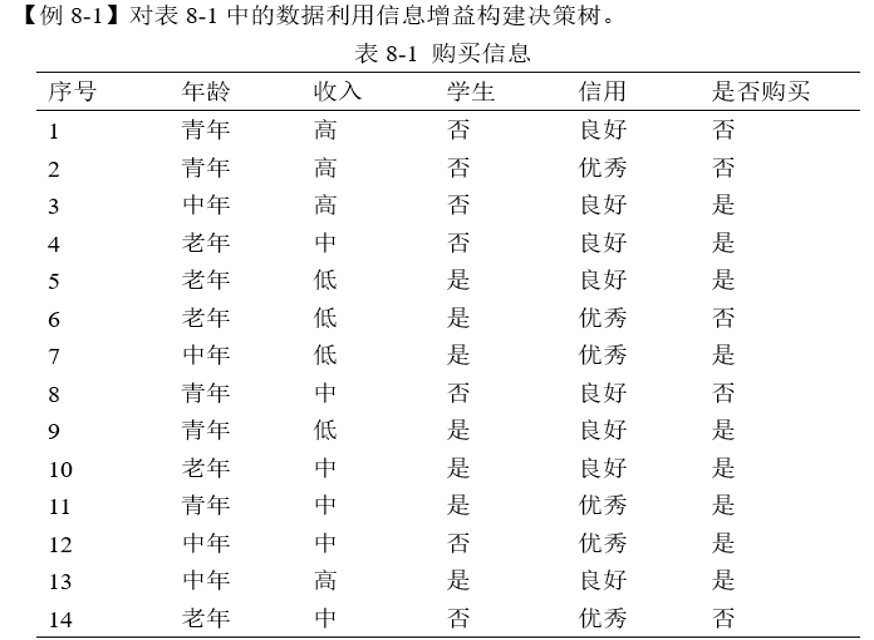
目标: 基于“年龄”、“收入”、“学生”、“信用”这4个属性,构建一个能预测“是否购买”的决策树。
ID3算法核心步骤回顾:👇
- 计算根节点(整个数据集)的熵。
- 对每个候选属性(年龄、收入、学生、信用),计算其信息增益。
- 选择信息增益最大的属性作为当前节点。
- 按该属性的取值分割数据集,对每个子集递归执行步骤1-3,直到满足终止条件(所有样本类别相同,或无属性可选)。
Step 1:计算根节点的熵 Entropy(S)
整个数据集 S 共有14条记录
目标变量“是否购买”的类别统计:
是:序号3,4,5,7,9,10,11,12,13 → 9条
否:序号1,2,6,8,14 → 5条
概率:p(是) = 9/14 ≈ 0.6429,p(否) = 5/14 ≈ 0.3571
熵:≈0.409+0.530=0.939
熵越大,系统的混乱程度越高,包含的信息量也越大(因为需要更多信息来使其变得确定)。熵越小,系统的纯度越高,确定性越强。
Step 2:计算每个属性的信息增益
我们需要分别计算 年龄、收入、学生、信用 这4个属性的信息增益,并选出最大的。
属性A1:年龄(取值:青年、中年、老年)
按“年龄”的3个取值分割数据集:
S1(青年):(序号1,2,8,9,11 → 共5条)
是:9,11 → 2条;否:1,2,8 → 3条
Entropy(S1) = 0.971
同理算出: S2(中年):Entropy(S2)=0;S3(老年):Entropy(S3)=0.971 👈👈
计算加权平均熵:
Entropy(S) = (5/14) * 0.971 + (5/14) * 0 + (5/14) * 0.971 = 0.694
信息增益 = GAIN(S,年龄)=Entropy(S)−平均熵=0.939−0.694=0.245
同样的步骤,我们算出其他3个属性的信息增益,并汇总:
GAIN(S,年龄)=0.939−0.694=0.245
Gain(S,收入)=0.939−0.9108=0.028
Gain(S,学生)=0.939−0.7875=0.1515
Gain(S,信用)=0.939−0.8916=0.0474
结论: 年龄的信息增益最大(0.245),选择年龄作为根节点! 👍👍
Step 3:对“年龄”的每个分支递归构建子树
根节点确定为“年龄”,其3个分支为“青年”、“中年”、“老年”。
Step 4:画出最终的决策树
[年龄?]
/ | \
青年/ 中年 \老年
/ | \
[学生?] [是] [信用?]
/ \ / \
是/ \否 良好 优秀
/ \ / \
[是] [否] [是] [否]决策树解读:
先看年龄: 👈
- 中年 → 直接买(全是“是”)。
- 老年 → 再看信用:
- 良好 → 买;优秀 → 不买。
- 青年 → 再看是否是学生:
- 是学生 → 买;不是学生 → 不买。
这个规则非常符合数据分布! 比如:
青年学生(9,11)→ 买;青年非学生(1,2,8)→ 不买。
老年信用良好(4,5,10)→ 买;老年信用优秀(6,14)→ 不买。
总结:ID3算法构建决策树的关键 👇
- 根节点选信息增益最大的属性(此处是“年龄”)。
- 对每个分支递归处理,同样选择剩余属性中信息增益最大的。
- 遇到“纯子集”(熵=0)则停止分裂,标记为叶子节点。
最终得到一个可解释性强的“if-else”规则集合。
ID3算法理论清晰,方法简单,学习能力较强。但也存在以下一些缺点: 👇
- (1)信息增益的计算依赖于特征数目较多的特征,而属性取值最多的属性并不一定最优。比如一个变量有2个值,各为1/2,另一个变量为3个值,各为1/3,其实他们都是完全不确定的变量,但是取3个值比取2个值的信息增益大。
- (2)ID3没考虑连续特征,比如长度、密度都是连续值,无法在ID3运用。
- (3)ID3算法是单变量决策树(在分支结点上只考虑单个属性),许多复杂概念的表达困难,属性相互关系强调不够,容易导致决策树中子树的重复或有些属性在决策树的某一路径上被检验多次;
- (4)算法的抗噪性差,训练例子中正例和反例的比例较难控制,而且没有考虑缺失值和过拟合问题。
4.C4.5算法
分类概述
Quinlan在1993年提出了ID3的改进版本C4.5算法。它与ID3算法的不同主要有以下几点。
C4.5 算法,作为在 ID3 算法上进行改进的算法,那么 C4.5 都在哪些方面改进了 ID3 呢?
1.采用信息增益率
因为 ID3 在计算的时候,倾向于选择取值多的属性。为了避免这个问题,C4.5 采用信息增益率 的方式来选择属性。
信息增益率 = 信息增益 / 属性熵.
当属性有很多值的时候,相当于被划分成了许多份,虽然信息增益变大了,但是对于 C4.5 来说,属性熵也会变大,所以整体的信息增益率并不大。
2.采用悲观剪枝
ID3 构造决策树的时候,容易产生过拟合 的情况。在 C4.5 中,会在决策树构造之后采用悲观剪枝(PEP),这样可以提升决策树的泛化能力。
悲观剪枝是后剪枝技术中的一种, 通过递归估算每个内部节点的分类错误率,比较剪枝前后这个节点的分类错误率来决定是否对其进行剪枝。这种剪枝方法不再需要一个单独的测试数据集。
3.离散化处理连续属性
C4.5 可以处理连续属性的情况,对连续的属性进行离散化的处理。比如打篮球存在的“湿度”属性,不按照“高、中”划分,而是按照湿度值进行计算,那么湿度取什么值都有可能。该怎么选择这个阈值呢,C4.5 选择具有最高信息增益的划分所对应的阈值。

4. 处理缺失值
针对数据集不完整的情况,C4.5 也可以进行处理
但是C4.5算法使用了熵模型,其中有大量耗时的对数运算,如果是连续值,还需要大量的排序工作,效率较低,且C4.5只能用于分类问题,不能用于回归问题。
C4.5核心工作是:
- 问一个问题,看能把数据分成几组。
- 衡量分组后,每组内部的“意见”是否统一(用信息熵)。
- 最终,在一个小组里,它通过“少数服从多数”的原则做出决定。
可以把C4.5看作一个专门为处理“投票”而设计的机器。
而回归任务需要是一个专门处理“数字”的机器。核心工作是:
- 问一个问题,把数据分成两组。
- 衡量分组后,每组内部的“数字”是否接近(用方差)
- 最终,在一个小组里,它通过“取平均值”来做出预测
5. CART算法
CART算法
CART算法,英文全称叫做 Classification And Regression Tree,中文叫做 分类回归树。
算法最早由Breiman等人提出,CART 算法(1984年提出,比 C4.5 早9年,但真正普及是在 C4.5 暴露缺点后)针对 C4.5 的痛点做了 “颠覆性优化”,成为现在工业界最主流的决策树算法。
ID3 和 C4.5 算法可以生成二叉树或多叉树,而 CART 只支持二叉树 。同时 CART 决策树比较特殊,既可以作分类树,又可以作回归树。
问题:什么是分类树和回归树呢?
- 分类树可以处理离散数据,也就是数据种类有限的数据,它输出的是样本的类别,
- 回归树可以对连续型的数值进行预测,也就是数据在某个区间内都有取值的可能,它输出的是一个数值。
CART算法用基尼系数代替熵模型。
经济学中,基尼系数是用来衡量一个国家收入差距的常用指标。当基尼系数大于 0.4 的时候,说明财富差异悬殊。基尼系数在 0.2-0.4 之间说明分配合理,财富差距不大。
因此,基尼系数越小,说明收入分配越平均。介入到机器学习中,说明样本差异性小,不确定程度低。
分类的过程本身是一个不确定度降低的过程,即纯度的提升过程。所以 CART 算法在构造分类树的时候,会选择基尼系数最小的属性 作为属性的划分。
假设 t 为节点,那么该节点的 GINI 系数的计算公式为:
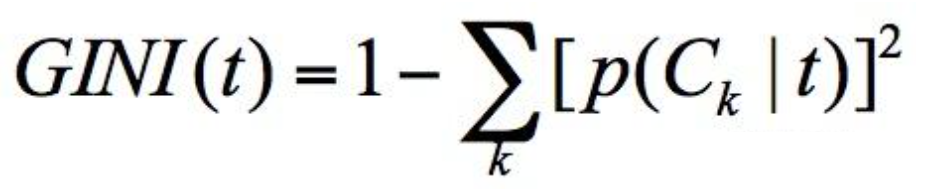
p(Ck|t) 表示节点 t 属于类别 Ck 的概率,节点 t 的基尼系数为 1 减去各类别 Ck 概率平方和
通过下面这个例子,我们计算一下两个集合的基尼系数分别为多少:

- 集合 1:6 个都去打篮球;
集合 1的基尼系数计算:所有人都去打篮球,所以 p(Ck|t)=1,因此 GINI(t)=1-1=0。 说明集合 1 的纯度很高,不存在任何不确定性。
- 集合 2:3 个去打篮球,3 个不去打篮球。
集合 2的基尼系数计算:有一半人去打篮球,而另一半不去打篮球,所以,p(C1|t)=0.5,p(C2|t)=0.5,GINI(t)=1-(0.50.5+0.50.5)=0.5。
通过两个基尼系数你可以看出,集合 1 的基尼系数最小,也证明样本最稳定,而集合 2 的样本不稳定性更大。
在 CART 算法中,基于基尼系数对特征属性进行二元分裂,假设属性 A 将节点 D 划分成了 D1 和 D2,如下图所示:
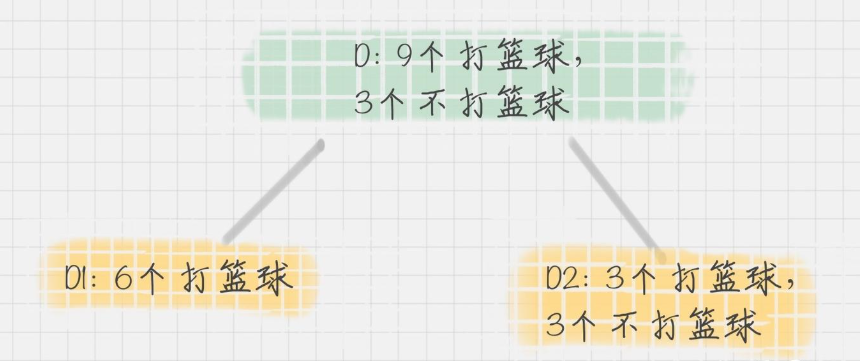
节点 D 的基尼系数等于子节点 D1 和 D2 的归一化基尼系数之和,用公式表示为:
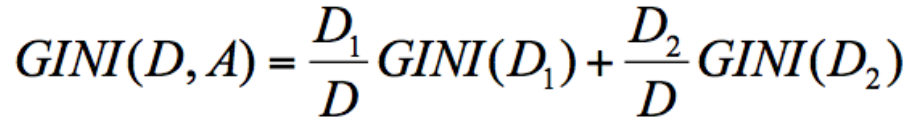
归一化基尼系数代表的是每个子节点的基尼系数乘以该节点占整体父亲节点 D 中的比例。
所以在属性 A 的划分下,节点 D 的基尼系数为: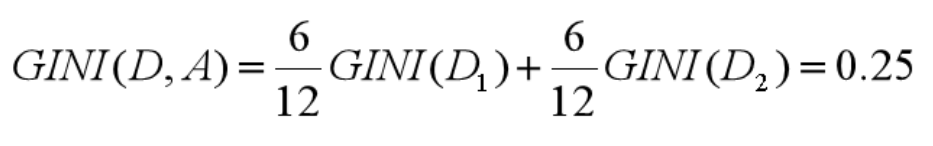
节点 D 被属性 A 划分后的基尼系数越大,样本集合的不确定性越大,也就是不纯度越高。
代码实操:👇
CART 分类树实际上是基于基尼系数来做属性划分的。在 Python 的 sklearn 中,如果我们想要创建 CART 分类树,可以直接使用 DecisionTreeClassifier 这个类。创建这个类的时候,默认情况下 criterion 这个参数等于 gini,也就是按照基尼系数来选择属性划分,即默认采用的是 CART 分类树。
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn import tree
from sklearn.model_selection import train_test_split
iris = load_iris() # 加载数据集
X_train,X_test,y_train,y_test=train_test_split(iris.data, iris.target,test_size=0.20,random_state=30,shuffle=True) # 划分训练集和测试集
clf = tree.DecisionTreeClassifier(criterion='entropy') # 创建CART分类树
# 设置criterion='entropy'时,是按照信息熵, 当criterion='gini'时,是按照基尼系数
# criterion缺省为'gini' 比起基尼系数, 信息熵对不纯度更加敏感,对不纯度的惩罚最强。但是在实际使用中,信息熵和基尼系数的效果基本相同。
clf = clf.fit(X_train,y_train)
plt.figure(dpi=150)
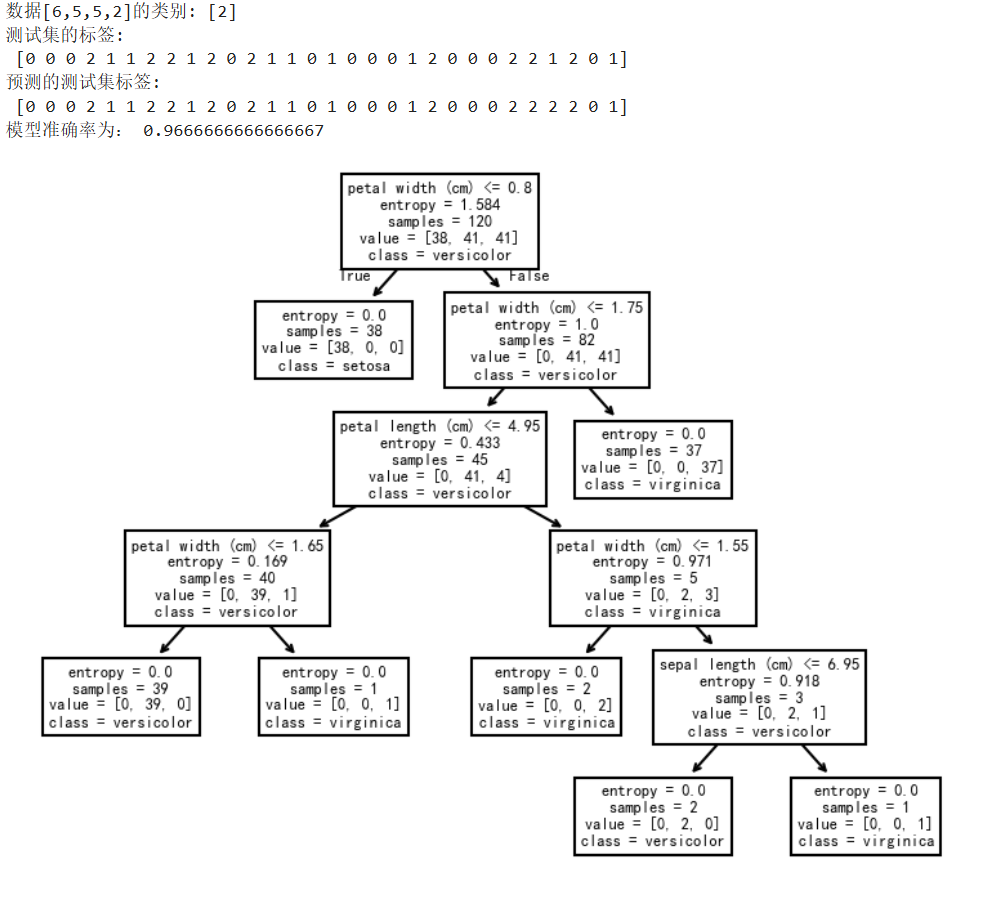
tree.plot_tree(clf, feature_names=iris.feature_names, class_names=iris.target_names)
# feature_names=iris.feature_names设置决策树中显示的特征名称
# 预测数据[6,5,5,2]的类别
print('数据[6,5,5,2]的类别:',clf.predict([[6,5,5,2]]))
print('测试集的标签:\n',y_test)
y_pre=clf.predict(X_test)
print('预测的测试集标签:\n',y_pre)
print('模型准确率为:',clf.score(X_test,y_test))可以修改criterion参数,看看效果,当criterion='entropy'时,是按照信息熵, 当criterion='gini'时,是按照基尼系数
6. KNN算法
KNN算法
K近邻(k-Nearest Neighbor Classification,KNN)算法是机器学习算法中最基础、最简单的算法之一,属于惰性学习法。
KNN算法:一句话讲明白核心思想
“物以类聚,人以群分”—— 一个样本的类别,由它周围最近的 K 个邻居的类别“投票”决定。
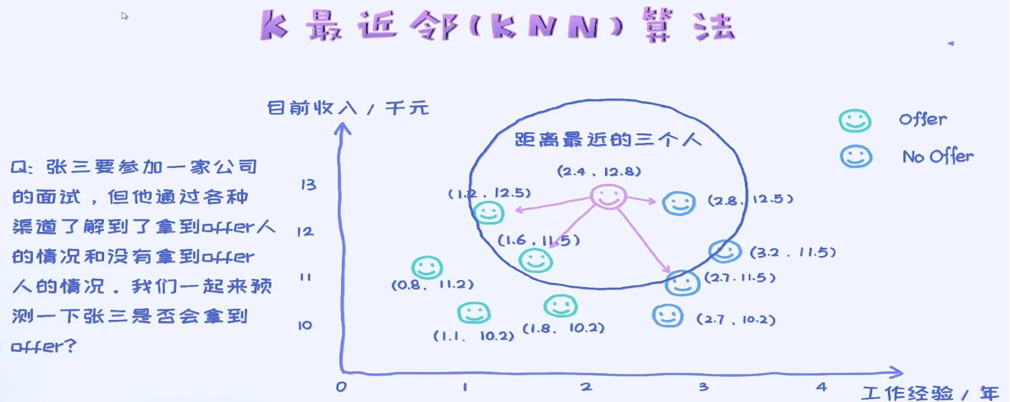
又比如:你新搬了小区,想知道邻居们是“安静派”还是“热闹派”。你只需看离你最近的 3 户(K=3)邻居,如果其中 2 户是“安静派”,那么你大概率也会被归为“安静派”。
2.KNN算法的3个核心步骤(超简单)
步骤1:算距离——“谁离我最近?”
计算目标样本与所有训练样本的 “距离”(常用 欧氏距离,类似“两点之间直线距离”)。
欧氏距离公式(二维数据): 样本 A(x1,y1) 和样本 B(x2,y2) 的距离
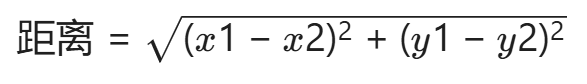
步骤2:找邻居——“选最近的K个”
按距离从小到大排序,选前 K 个样本(最近的 K 个邻居)。
步骤3:投票——“少数服从多数”
统计 K 个邻居的类别,出现次数最多的类别就是目标样本的预测类别。
3.Python案例:用KNN分类“红蓝点”数据
我们用一个二维散点图(横轴x,纵轴y)模拟数据,其中:
蓝色点:类别0
红色点:类别1
绿色点:待预测的新样本
目标:用KNN预测绿色点属于哪一类。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier # 导入KNN模型
plt.rcParams['font.family']=['SimHei'] #用来正常显示中文
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
# ------------------------------------------------------
# 1. 准备数据(生成红蓝点+绿色待预测点)
# ------------------------------------------------------
# 生成类别0(蓝色点):中心(2,2),随机分布
np.random.seed(42) # 固定随机数,结果可复现
class0 = np.random.normal(loc=[2, 2], scale=0.8, size=(30, 2)) # 30个样本,均值(2,2),标准差0.8
# 生成类别1(红色点):中心(6,6),随机分布
class1 = np.random.normal(loc=[6, 6], scale=0.8, size=(30, 2))
# 待预测的绿色点
new_point = np.array([[4, 4]]) # 二维坐标(4,4)
# 合并数据:特征X(所有点的坐标)和标签y(0=蓝色,1=红色)
X = np.vstack([class0, class1]) # 合并两个类别的特征
y = np.hstack([np.zeros(30), np.ones(30)]) # 标签:前30个0,后30个1
# ------------------------------------------------------
# 2. 训练KNN模型(K=5,选最近的5个邻居)
# ------------------------------------------------------
k = 5 # K值(可调,试试k=1、3、7的效果)
knn = KNeighborsClassifier(n_neighbors=k) # 初始化KNN模型
knn.fit(X, y) # 训练(KNN是“惰性学习”,训练时仅存储数据)
# 预测新样本类别
predicted_class = knn.predict(new_point)
print(f"K={k}时,绿色点预测类别:{'红色 (类别1)' if predicted_class[0]==1 else '蓝色 (类别0)'}")
# ------------------------------------------------------
# 3. 可视化结果(散点图+新样本+K个邻居)
# ------------------------------------------------------
plt.figure(figsize=(8, 6))
# 绘制所有训练样本
plt.scatter(class0[:, 0], class0[:, 1], c='blue', label='类别0(蓝色)', alpha=0.6)
plt.scatter(class1[:, 0], class1[:, 1], c='red', label='类别1(红色)', alpha=0.6)
# 绘制待预测点
plt.scatter(new_point[0, 0], new_point[0, 1], c='green', s=200, marker='*', label='待预测点')
# 找到新点的K个最近邻居并标记
distances, indices = knn.kneighbors(new_point) # 返回距离和邻居的索引
plt.scatter(X[indices, 0], X[indices, 1], c='purple', s=100, marker='o', facecolors='none', label=f'最近{k}个邻居')
# 美化图形
plt.xlabel('X坐标')
plt.ylabel('Y坐标')
plt.title(f'KNN分类 (K={k}):绿色点属于{predicted_class[0]}类')
plt.legend()
plt.grid(alpha=0.3)
plt.show()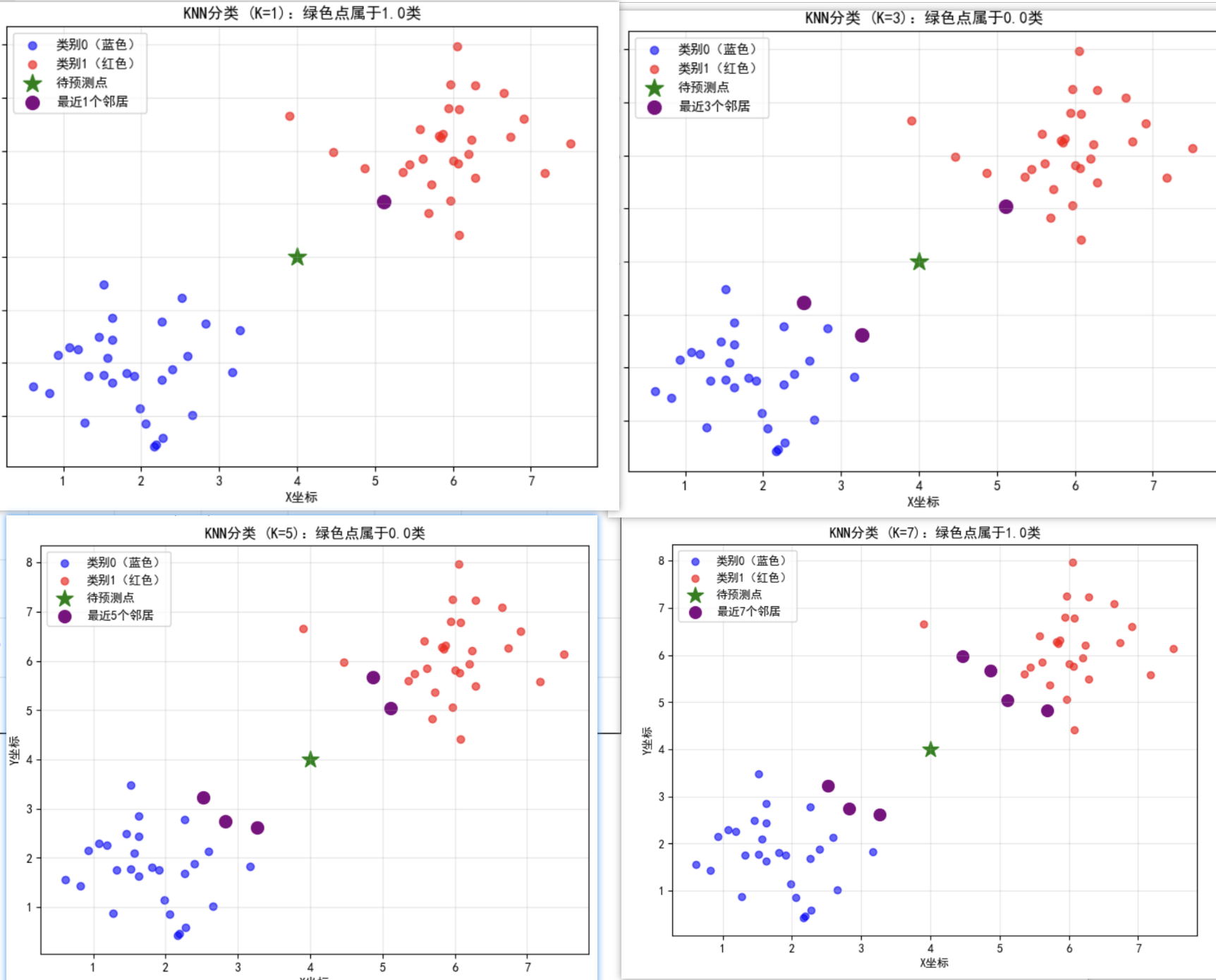
代码运行结果解读: 👇
数据分布:蓝色点聚集在(2,2)附近,红色点聚集在(6,6)附近,绿色点在(4,4)(两类中间)。
K=5时:绿色点的5个邻居中,蓝色点比红色点多(从图中紫色圈可看出),因此预测为 蓝色(类别1)。
试试改K值:👇
K=1:最近的1个邻居是红色点 → 预测红色。
K=7:可能蓝色和红色邻居数量接近,预测结果可能变化。
KNN的关键:K值怎么选?
K太小(如K=1):容易受噪声点影响(过拟合)。
K太大(如K=样本总数):所有样本投票,类别由多数类决定(欠拟合)。
最佳K值:通过交叉验证(如5折CV)选择验证集准确率最高的K(常用K=3、5、7)。
KNN的优缺点?
优点:
- 超简单:原理就是“找邻居投票”,几乎不用懂数学。
- 无需训练:是“惰性学习”,训练时只需存储数据,预测时才计算距离。
- 适合多分类:天然支持多个类别(如K=5,3个A类、2个B类 → 预测A类)。
缺点: - 预测慢:对每个新样本,需计算与所有训练样本的距离(数据量大时卡到爆)。
- 对异常值敏感:如果有离群点(如红色点跑到蓝色区域),可能误导K个邻居。
- 依赖距离计算:特征量纲不同时需先标准化(如体重单位是kg vs g,距离会被体重主导)。
这个案例用二维数据直观展示了KNN的核心逻辑,实际应用中特征可能有很多维度(如100个特征),但原理完全一样
教材中的案例:👇
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:,:2] #取前两列特征
Y = iris.target#取标签
print(iris.feature_names) #打印特征名称
cmap_light = ListedColormap(['#FFAAAA','#AAFFAA','#AAAAFF']) #定义颜色
cmap_bold = ListedColormap(['#FF0000','#00FF00','#0000FF']) #定义颜色
clf = KNeighborsClassifier(n_neighbors = 10,weights = 'uniform') #定义KNN模型 weights = 'uniform' 表示权重相同 n_neighbors = 10 表示选取最近的10个
clf.fit(X,Y) #训练模型
#画出决策边界
x_min,x_max = X[:,0].min()-1,X[:,0].max()+1 #x轴的最小值和最大值
y_min,y_max = X[:,1].min()-1,X[:,1].max()+1 #y轴的最小值和最大值
xx,yy = np.meshgrid(np.arange(x_min,x_max,0.02), #生成网格数据
np.arange(y_min,y_max,0.02))
Z = clf.predict(np.c_[xx.ravel(),yy.ravel()]).reshape(xx.shape) #预测结果
#画出图像
plt.figure()
plt.pcolormesh(xx,yy,Z,cmap = cmap_light)
#绘制预测结果图
plt.scatter(X[:,0],X[:,1],c = Y,cmap = cmap_bold)
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title('3_Class(k = 10,weights = uniform)')
plt.show()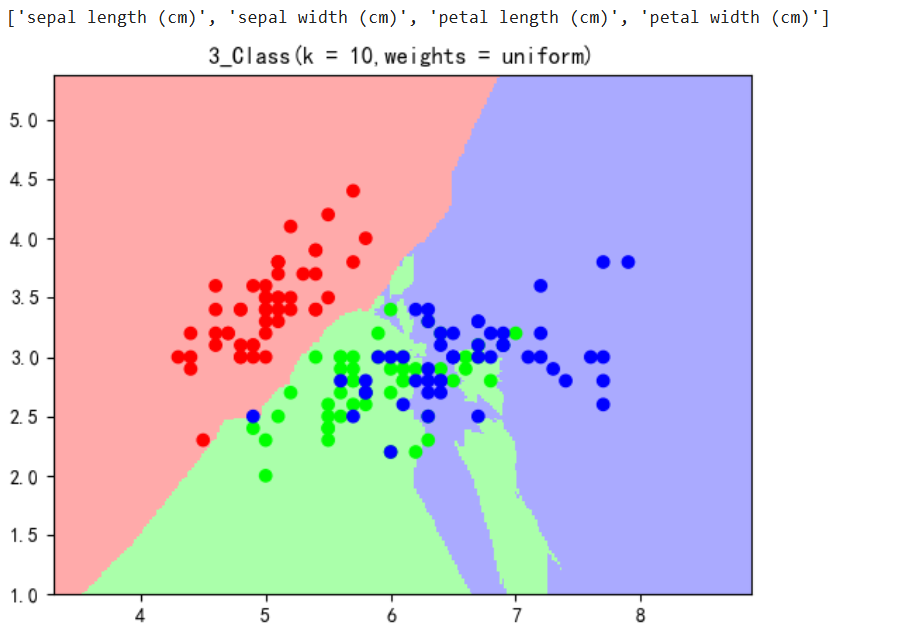
sepal 花萼
petal 花瓣
7. 支持向量机
支持向量机
1. 支持向量机(SVM)的概要
支持向量机(SVM)听起来高大上,但核心思想其实很简单:
找一条线,把两类数据分得最开。
找到一个分隔超平面,使得两类数据中离平面最近的点(支持向量)到平面的距离(间隔)最大。
“最大间隔”:直线两边留出的“安全距离”最大,这样新数据来了不容易分错(泛化能力强)。
“支持向量”:离分隔线最近的那些样本点(是决定分隔线位置的“关键少数”)。
用“班级座位”理解SVM 👇
想象一个教室,左边坐“男生”,右边坐“女生”,中间有一条过道(分隔线)。
目标:过道要足够宽,两边同学离过道的距离尽量远(避免挤到一起)。
支持向量: 过道两边离过道最近的那几个同学(他们的位置决定了过道的宽度)。
SVM做的就是:找到这条最宽的过道(最大间隔分隔线)
2.SVM 3个核心概念
超平面:一条直线(1维)、平面(2维)、超平面(n维)。
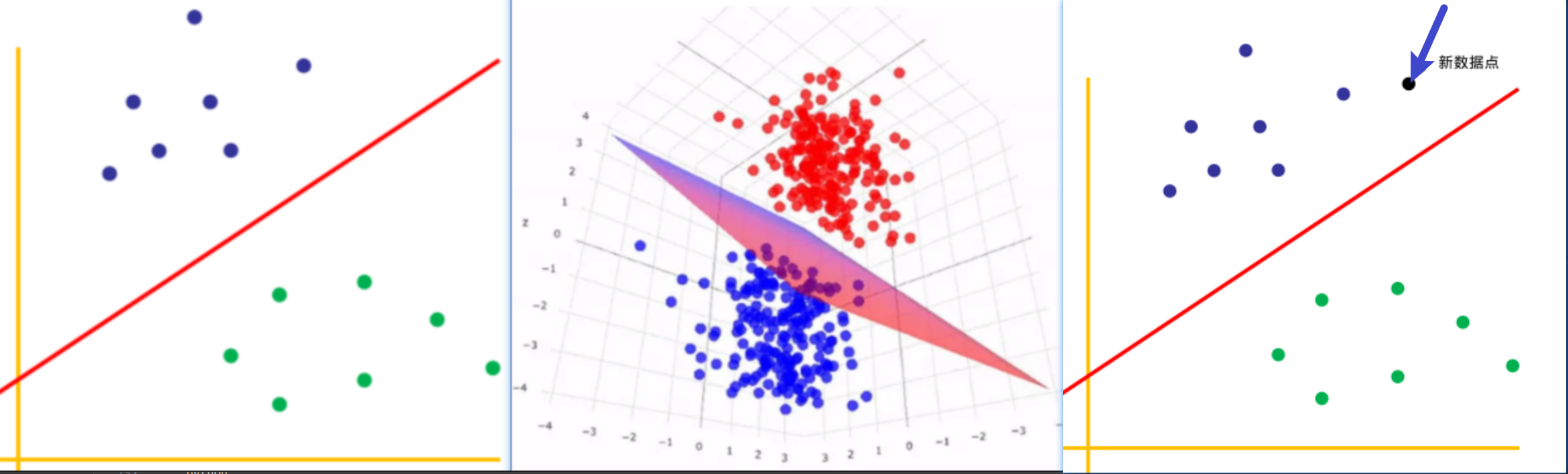
- 在二维空间中,超平面只是将数据点分为两类的直线,如下图的红色直线:
- 在三维空间中,超平面是将数据点分为两类的平面,如下图的红色平面:
- 同样,在 N 维空间中,超平面是具有 (N-1) 维的空间。
SVM的分类思想是通过评估新数据点落在超平面的哪一侧进行分类,如下图,若新数据点(黑色)位于超平面的上面,则该点属于蓝色类;若位于超平面的下面,则属于绿色类。
间隔:(Margin)是超平面与来自每个类的最近数据点之间的距离,SVM 的目标是最大化这一间隔,同时尽量减少分类错误。
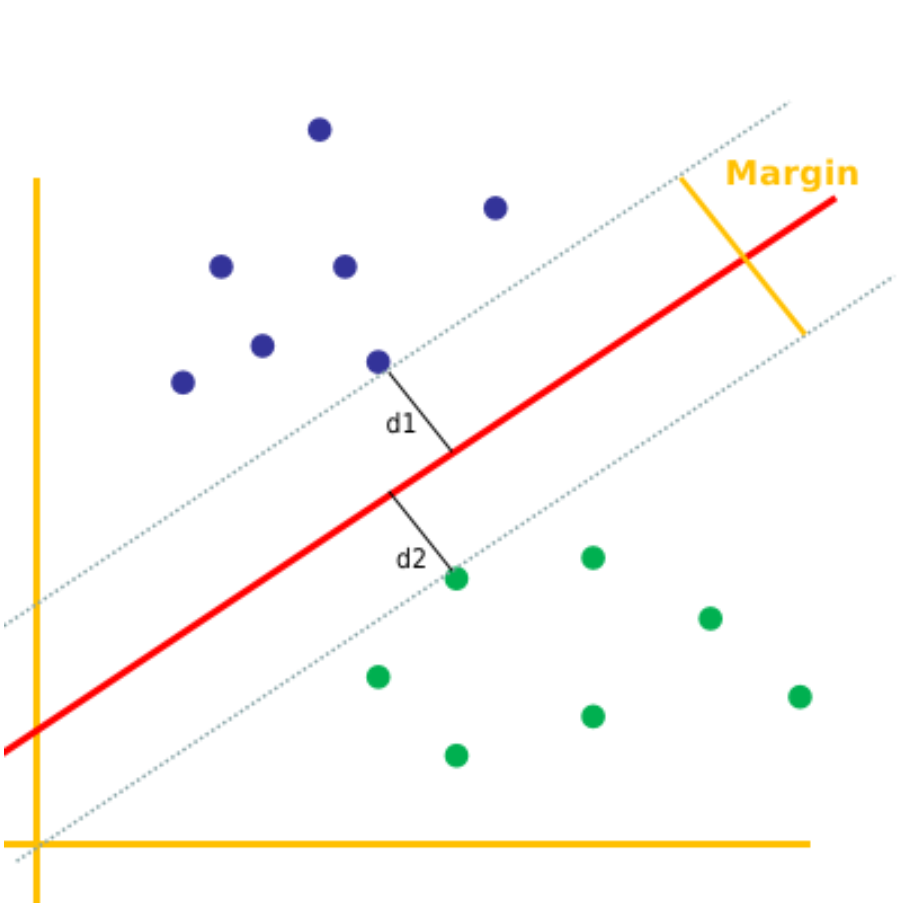
较大的间隔表明分类的置信度较高,因为这意味着决策边界与来自每个类别的最近数据点之间的距离较大。SVM 的设计旨在找到最大化间隔的超平面,
置信度:预测的置信度越高,则预测的准确性越高。
支持向量 (support vector)是最靠近决策边界(超平面)的数据点。这些数据点非常重要,因为它们决定了超平面的位置和方向,从而对 SVM 的分类准确性产生重大影响。实际上,SVM 之所以命名为支持向量机,是因为这些支持向量“支持”或定义了决策边界。支持向量用于计算间隔(Margin),也就是超平面与来自每个类别的最近数据点之间的距离之和。SVM 的目标是最大化这一间隔,同时尽量减少分类错误。
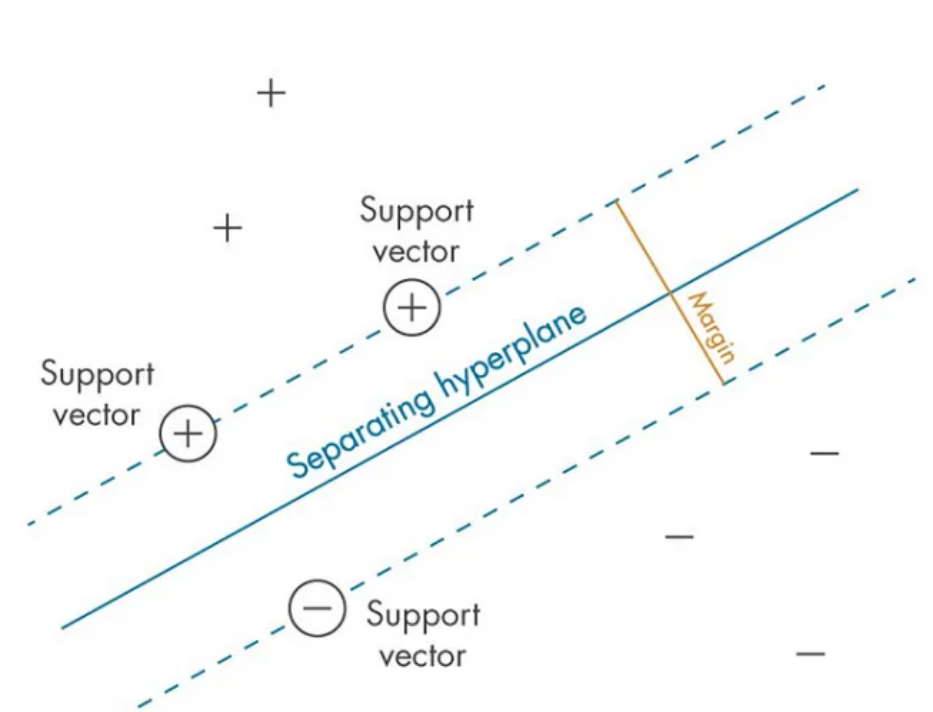
3.SVM2种情况
3.1 线性可分
线性可分:数据完全可分,可以用一条直线(超平面)分隔。

3.2 线性不可分
线性不可分:数据点无法用一条直线分隔。
4.Python案例:用SVM分隔“红蓝点”(可视化最大间隔)✏️ 👇
我们用和KNN一样的“红蓝点”数据(蓝色点聚在(2,2),红色点聚在(6,6)),看看SVM如何找到“最宽过道”。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC # SVM分类器
from sklearn.datasets import make_blobs # 生成模拟数据
# ------------------------------------------------------
# 1. 生成模拟数据(和KNN案例类似,蓝色点和红色点)
# ------------------------------------------------------
# 生成两类数据,中心点分别为(2,2)和(6,6),标准差0.8
X, y = make_blobs(
n_samples=60, # 60个样本
centers=[[2, 2], [6, 6]], # 两个中心点
cluster_std=0.8, # 标准差,控制数据分散程度
random_state=42 # 固定随机数,保证结果一致
)
# ------------------------------------------------------
# 2. 训练SVM模型(线性核函数,寻找最大间隔直线)
# ------------------------------------------------------
# SVM参数:C=1.0(惩罚系数,控制是否允许样本在间隔内,C越小间隔越大但允许更多样本越界)
# kernel='linear'(线性核,适用于线性可分数据)
svm = SVC(kernel='linear', C=1.0, random_state=42)
svm.fit(X, y) # 训练SVM(找到最大间隔分隔线)
# ------------------------------------------------------
# 3. 获取SVM关键信息(分隔线、支持向量)
# ------------------------------------------------------
# 分隔线方程:w0*x0 + w1*x1 + b = 0 → x1 = (-w0/w1)x0 - b/w1
w = svm.coef_[0] # 法向量w([w0, w1])
b = svm.intercept_[0] # 截距b
support_vectors = svm.support_vectors_ # 支持向量(离分隔线最近的点)
print(f"分隔线方程:{w[0]:.2f}*x0 + {w[1]:.2f}*x1 + {b:.2f} = 0")
print(f"支持向量数量:{len(support_vectors)}个(决定分隔线位置的关键点)")
# ------------------------------------------------------
# 4. 可视化:分隔线+间隔+支持向量
# ------------------------------------------------------
plt.figure(figsize=(8, 6))
# 绘制所有样本点
plt.scatter(X[y==0][:,0], X[y==0][:,1], c='blue', label='类别0(蓝色)', alpha=0.6)
plt.scatter(X[y==1][:,0], X[y==1][:,1], c='red', label='类别1(红色)', alpha=0.6)
# 绘制支持向量(用黑色圆圈标出)
plt.scatter(support_vectors[:,0], support_vectors[:,1], s=150, linewidth=2, facecolors='none', edgecolors='black', label='支持向量')
# 绘制分隔线(w·x + b = 0)
x0 = np.linspace(X[:,0].min()-1, X[:,0].max()+1, 100) # x轴取值范围
x1_sep = (-w[0]/w[1])*x0 - b/w[1] # 根据分隔线方程计算x1
plt.plot(x0, x1_sep, 'k-', label='分隔线')
# 绘制间隔边界(支持向量所在的线,w·x + b = ±1)
x1_up = (-w[0]/w[1])*x0 - (b-1)/w[1] # 上边界(+1)
x1_down = (-w[0]/w[1])*x0 - (b+1)/w[1] # 下边界(-1)
plt.plot(x0, x1_up, 'k--', label='间隔边界')
plt.plot(x0, x1_down, 'k--')
# 美化图形
plt.xlabel('x0坐标')
plt.ylabel('x1坐标')
plt.title('SVM分类(线性核):最大间隔分隔线与支持向量')
plt.legend()
plt.grid(alpha=0.3)
plt.xlim(X[:,0].min()-1, X[:,0].max()+1)
plt.ylim(X[:,1].min()-1, X[:,1].max()+1)
plt.show()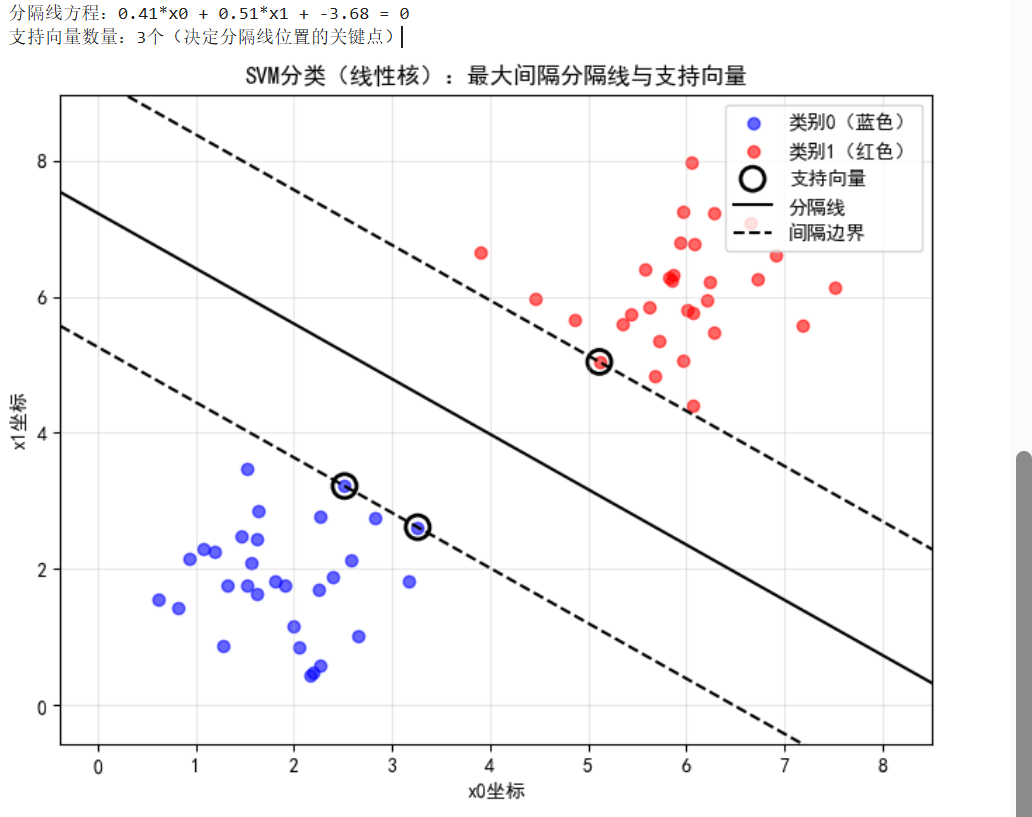
运行结果解读 👇
分隔线 :黑色实线,完美分开蓝色和红色点。
间隔边界:黑色虚线,两条线之间的距离就是“最大间隔”,支持向量(黑色空心圆)刚好落在这两条线上。
支持向量:离分隔线最近的点(通常数量很少),是SVM的“决策核心”——即使去掉其他点,只要支持向量还在,分隔线就不变!
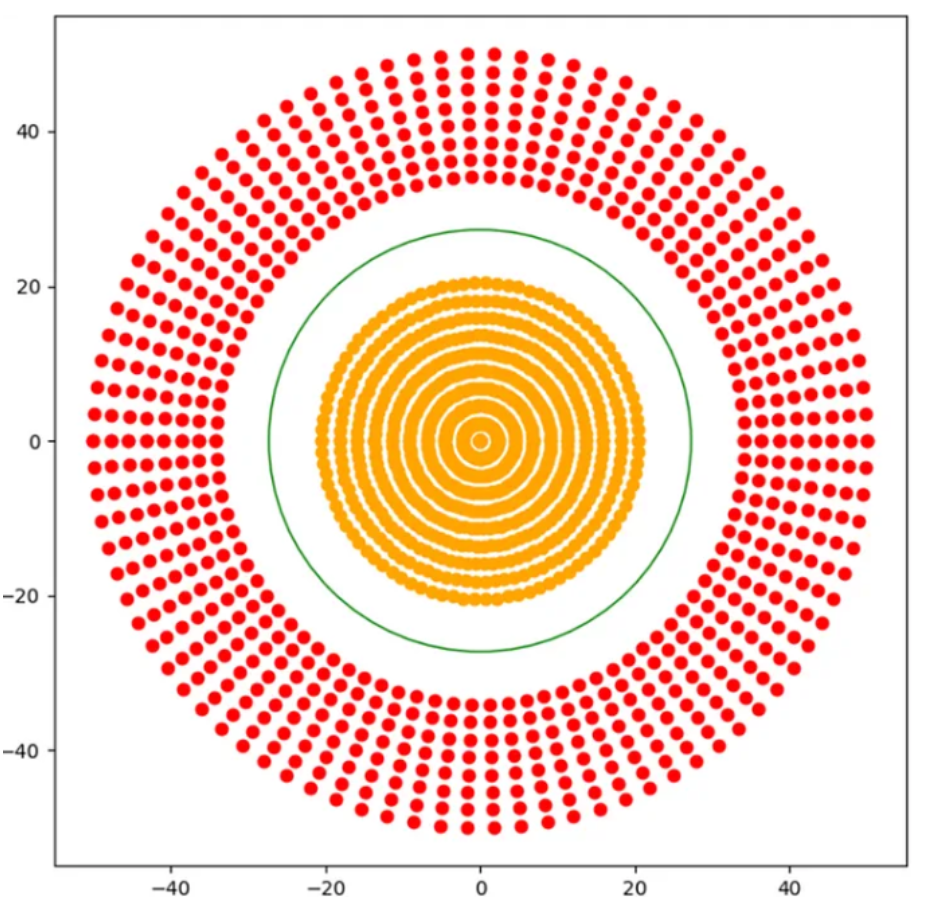
上面例子中数据是“线性可分”的(一条直线能分开)。但如果数据长这样呢?
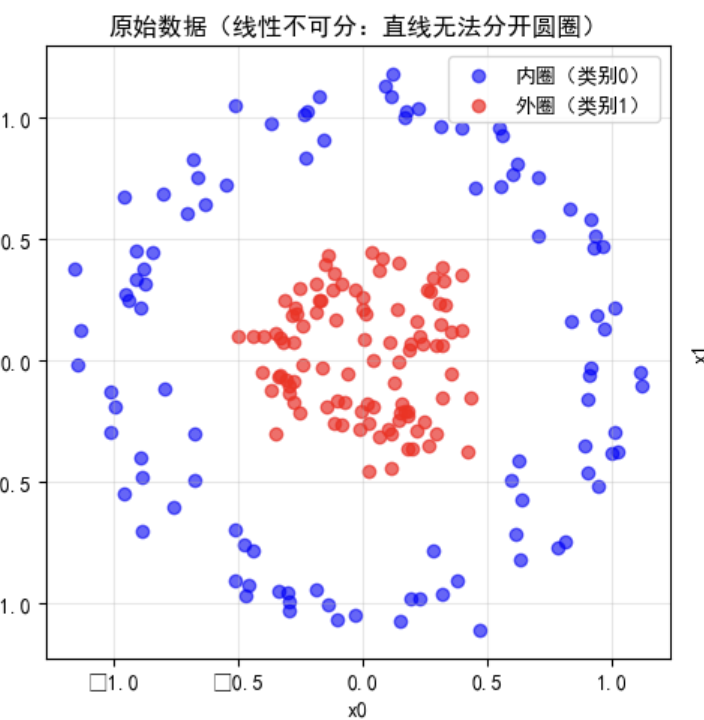
(红色点在圆圈内,蓝色色点在圆圈外,直线分不开)
SVM的解决方案:核函数(Kernel Trick)
核心思想:把低维非线性数据“映射”到高维空间,让数据在高维空间变得线性可分。
常用核函数:
线性核(linear) :用于线性可分数据(如上面的例子)。
高斯核(RBF) :最常用,能处理各种非线性数据(如圆圈分布、月牙分布)。
多项式核(poly) :用于特征之间有多项式关系的数据。
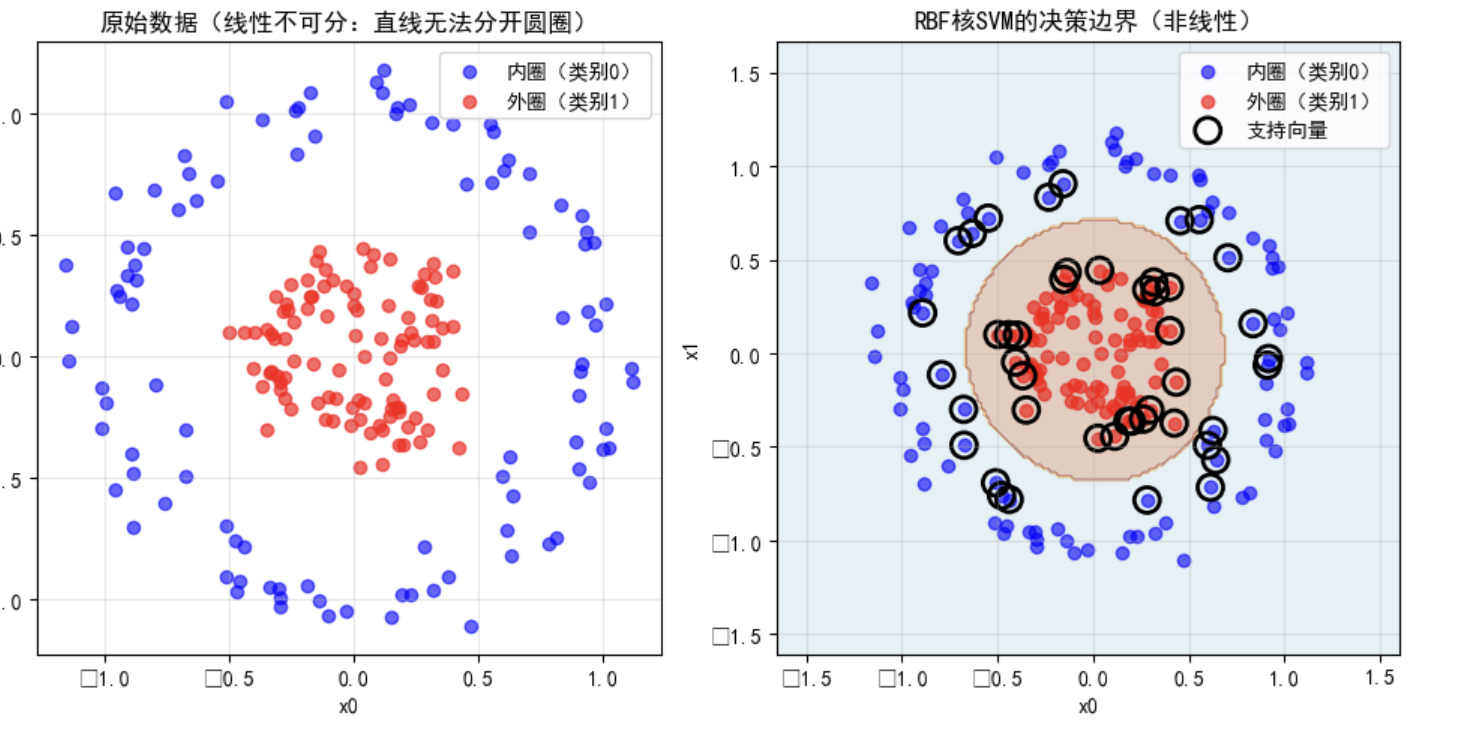
**通俗类比:**低维空间的“弯曲线” = 高维空间的“直线”。核函数就像“放大镜”,帮我们在高维空间找到那条“分隔直线”。
SVM的优缺点 👇
优点:
- 泛化能力强 :通过“最大间隔”原则,对新数据的预测更稳定(不容易过拟合)。
- 对高维数据友好 :在特征数远大于样本数时(如文本分类,特征是词汇表),表现依然优秀。
- 决策过程透明 :支持向量清晰可见,可解释性强。
缺点 - 计算量大:训练时依赖支持向量,数据量太大(如百万级样本)会很慢(需用简化版SVM)。
- 调参复杂:核函数选择、惩罚系数C、高斯核的gamma参数等,需要交叉验证仔细调参。
- 不直接输出概率:默认只输出类别,如需概率需额外训练(probability=True)。
总结
课堂作业
SVM是个‘追求极致的完美主义者’——它不满足于随便找条线分开数据,而是要找到那条‘最宽的过道’,并用最少的‘关键样本’(支持向量)来决策。遇到非线性数据时,它还会用‘核函数放大镜’把数据变成立可分的!
8. 朴素贝叶斯分类
朴素贝叶斯分类
贝叶斯分类是一类分类算法总称,这类算法均已“贝叶斯定理”为基础,采用概率推理方法。
朴素贝叶斯(Naive Bayes)是基于 “概率论” 的分类算法,核心思想超简单——根据已知概率,猜最可能的结果。
8.1朴素贝叶斯核心思想:
我们用“邮件分类(垃圾邮件/正常邮件)”的例子来说明:
“已知某件事发生了(如邮件中出现‘免费’‘中奖’等词),反过来算这件事属于某个类别的概率(垃圾邮件概率有多大),概率最大的那个类别就是预测结果。”
用公式概括(贝叶斯定理):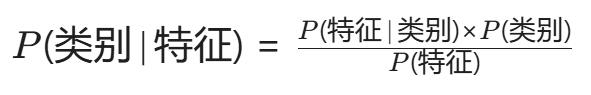
目标: 计算不同类别的后验概率P(类别∣特征),选概率最大的类别。
“朴素”的含义:假设特征之间 相互独立(如邮件中“免费”和“中奖”出现的概率互不影响),大大简化计算。
8.2 朴素贝叶斯分类流程:
用“猜球游戏”理解朴素贝叶斯 👇
场景: 两个袋子,里面装着红球和蓝球:
袋子A(垃圾邮件): 红球(“免费”词)3个,蓝球(“正常”词)1个。
袋子B(正常邮件): 红球1个,蓝球3个。
已知:随机选一个袋子,摸出了1个红球(特征:出现“免费”词)。
问题:这个红球来自袋子A(垃圾邮件)的概率大,还是袋子B(正常邮件)的概率大?
用贝叶斯定理计算:
1.先验概率 P(类别):
P(A)=0.5(选袋子A的概率),
P(B)=0.5(选袋子B的概率)
2. 似然概率 P(特征∣类别):
袋子A摸出红球:P(红球∣A)=3/4。
袋子B摸出红球:P(红球∣B)=1/4。
3. 后验概率 P(类别∣特征):
P(A∣红球)= P(红球∣A)P(A) / P(红球)=(3/4×0.5) / P(红球)
P(B∣红球)= P(红球∣B)P(B) / P(红球)=(1/4×0.5) / P(红球)
因为分母 P(红球) 相同,比较分子:P(A∣红球)>P(B∣红球) 也就是(3/4×0.5)>(1/4×0.5), 所以 红球更可能来自袋子A(垃圾邮件)。
8.4Python案例:用朴素贝叶斯分类“邮件文本”
我们用简单的文本数据模拟邮件分类,特征是“是否出现特定关键词”,目标是预测“是否为垃圾邮件”。
import numpy as np
import pandas as pd # 新增:之前代码漏了导入pandas,这里补上
import matplotlib.pyplot as plt
from sklearn.naive_bayes import BernoulliNB
from sklearn.preprocessing import LabelEncoder
# ------------------------------------------------------
# 1. 准备数据(邮件分类案例)
# ------------------------------------------------------
data = {
'邮件内容': [
'免费中奖点击', # 垃圾邮件
'中奖信息点击', # 垃圾邮件
'工作汇报文档', # 正常邮件
'免费资料下载', # 垃圾邮件
'会议时间通知' # 正常邮件
],
'免费': [1, 0, 0, 1, 0], # 特征1:是否有“免费”
'中奖': [1, 1, 0, 0, 0], # 特征2:是否有“中奖”
'点击': [1, 1, 0, 0, 0], # 特征3:是否有“点击”
'是否垃圾邮件': ['是', '是', '否', '是', '否'] # 目标标签
}
df = pd.DataFrame(data)
# 标签编码:将“是/否”转为1/0
le = LabelEncoder()
df['是否垃圾邮件'] = le.fit_transform(df['是否垃圾邮件']) # 是→1,否→0
# 提取特征X和目标y
X = df[['免费', '中奖', '点击']]
y = df['是否垃圾邮件']
# ------------------------------------------------------
# 2. 训练朴素贝叶斯模型(伯努利贝叶斯)
# ------------------------------------------------------
nb = BernoulliNB()
nb.fit(X, y)
# ------------------------------------------------------
# 3. 预测新邮件
# ------------------------------------------------------
new_email = np.array([[1, 0, 1]]) # 新邮件特征:免费=1,中奖=0,点击=1
pred_proba = nb.predict_proba(new_email) # [正常概率, 垃圾概率]
pred_class = nb.predict(new_email)
print(f"新邮件特征(免费=1, 中奖=0, 点击=1)")
print(f"正常邮件概率:{pred_proba[0][0]:.2%}")
print(f"垃圾邮件概率:{pred_proba[0][1]:.2%}")
print(f"预测结果:{'垃圾邮件' if pred_class[0]==1 else '正常邮件'}")
# ------------------------------------------------------
# 4. 可视化(修复先验概率计算方式)
# ------------------------------------------------------
plt.figure(figsize=(10, 6))
# 左图:先验概率 P(类别)(改用class_count_计算)
class_counts = nb.class_count_ # 每个类别的样本数量([正常邮件数, 垃圾邮件数])
prior_probs = class_counts / np.sum(class_counts) # 先验概率 = 类别数量/总样本数
plt.subplot(1, 2, 1)
plt.bar(['正常邮件 (0)', '垃圾邮件 (1)'], prior_probs, color=['green', 'red'], alpha=0.7)
plt.title('先验概率 P(类别)')
plt.ylabel('概率')
plt.ylim(0, 1)
# 右图:条件概率 P(特征|类别)(直接用feature_log_prob_转换为概率)
# feature_log_prob_存储的是对数概率,需用np.exp转换为原始概率
normal_probs = np.exp(nb.feature_log_prob_[0]) # 正常邮件下特征出现的概率
spam_probs = np.exp(nb.feature_log_prob_[1]) # 垃圾邮件下特征出现的概率
features = ['免费', '中奖', '点击']
x = np.arange(len(features))
width = 0.35
plt.subplot(1, 2, 2)
plt.bar(x - width/2, normal_probs, width, label='正常邮件', color='green', alpha=0.7)
plt.bar(x + width/2, spam_probs, width, label='垃圾邮件', color='red', alpha=0.7)
plt.xticks(x, features)
plt.title('后验概率 P(特征|类别)')
plt.ylabel('特征出现的概率')
plt.ylim(0, 1)
plt.legend()
plt.tight_layout()
plt.show()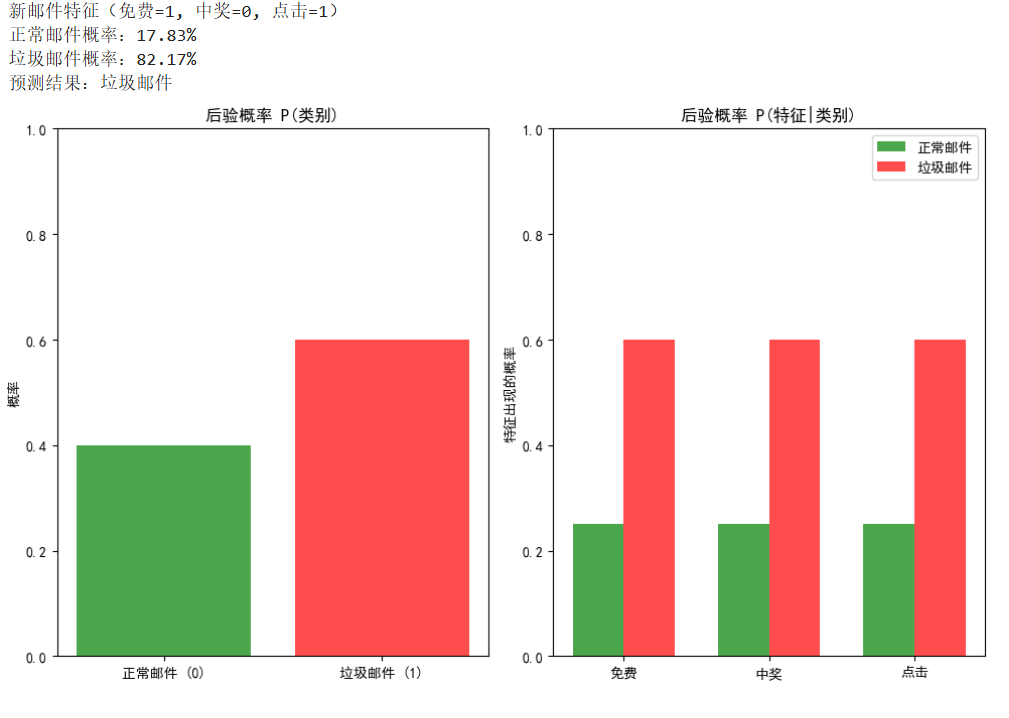
代码运行结果解读:
先验概率:训练集中垃圾邮件占比 3/5=60%(红色柱),正常邮件占比 40%(绿色柱)。
后验概率:
垃圾邮件中,“免费”出现概率=2/3(3封垃圾邮件中2封有“免费”),“点击”出现概率=2/3。
正常邮件中,所有关键词出现概率=0(因为正常邮件中没有这些词)。
新邮件预测:
由于新邮件包含“免费”和“点击”,在垃圾邮件中的条件概率远高于正常邮件,因此 垃圾邮件概率≈82.17%,预测为垃圾邮件。
朴素贝叶斯的优缺点
优点 👇
- 速度快:训练时只需计算概率,预测时只需做乘法和比较,适合大数据(如实时垃圾邮件过滤)。
- 对小样本友好:即使数据少,概率估算也能稳定进行(可通过“拉普拉斯平滑”避免概率为0)。
- 解释性强:每个特征对类别的“贡献”(概率)清晰可见。
缺点 👇 - 特征独立假设太“朴素”:现实中特征常不独立(如“免费”和“中奖”往往同时出现),可能导致预测不准。
- 对特征分布敏感:假设特征服从某种分布(如伯努利分布、高斯分布),若实际分布不符,效果下降。
一句话总结朴素贝叶斯
“朴素贝叶斯是个‘概率计算器’——它用已知的类别概率和特征概率,反过来推算‘当前特征最可能属于哪个类别’,虽然假设特征独立有点‘天真’,但胜在简单快准,是处理文本分类、垃圾邮件过滤的‘性价比之王’!”
下次遇到“根据多个特征猜类别”的问题(如疾病诊断、用户画像分类),朴素贝叶斯会是你的首选工具之一~
朴素贝叶斯三兄弟:核心区别对比表
| 类型 | 特征分布假设 | 适用特征类型 | 核心参数 | 典型应用场景 | ** |
|---|---|---|---|---|---|
| 伯努利朴素贝叶斯 | 特征是0/1二值变量(是否出现) | 文本(词是否出现)、是否点击、是否购买等 | alpha(平滑系数) | 垃圾邮件过滤、点击率预测 | |
| 多项式朴素贝叶斯 | 特征是非负整数计数(出现次数) | 文本(词频)、商品购买数量、用户点击次数 | alpha(平滑系数) | 文本分类(TF-IDF特征)、主题识别 +alpha\times\text{特征数}} $$(拉普拉斯平滑)` | |
| 高斯朴素贝叶斯 | 特征是连续值(服从正态分布) | 身高、体重、温度、图像像素值等连续数据 | 无(自动计算均值/标准差) | 身高体重分类、疾病诊断(医疗指标)、图像识别 |
关键结论:如何选择?
- 看特征类型:
- 二值特征(0/1)→ 伯努利
- 计数特征(次数)→ 多项式
- 连续特征(实数)→ 高斯
- 核心共性:均基于“贝叶斯定理+特征独立假设”,训练速度快,适合大数据场景。
一句话总结
“朴素贝叶斯三兄弟,核心都是‘贝叶斯+独立假设’,区别只在对特征的‘概率分布’假设:
高斯:特征是连续值(如身高),假设像“正态分布”;
多项式:特征是计数(如词频),假设像“骰子点数分布”;
伯努利:特征是0/1(如词是否出现),假设像“抛硬币分布”。
选对“分布”= 用对工具,数据类型匹配时,朴素贝叶斯永远是“简单快准”的首选!”
9. 模型评估和选择
模型评估与选择——像医生看病一样评价你的分类模型
理解我们如何知道一个分类模型(比如判断邮件是“垃圾邮件”还是“正常邮件”)是好是坏。
掌握几个关键的评估“尺子”:准确率、精确率、召回率。
学习两种让模型变得更“通用”的技巧:正则化和交叉验证。
9.1模型好坏怎么看?—— 混淆矩阵
想象一下,你是一位医生,你的任务是判断一个人是否得了某种病(比如流感)。 你的诊断(模型预测)和真实情况(真实标签)会有四种可能的结果:
为了清晰地展示这四种结果,我们用一个叫做 混淆矩阵(Confusion Matrix) 的表格来总结。
| 模型预测 | 真实情况:生病 (Positive) | 真实情况:健康 (Negative) |
|---|---|---|
| 模型预测:生病 (Positive) | 真正例 (TP) (你猜对了,他真病了) | 假正例 (FP) (你猜错了,误诊了健康人) |
| 模型预测:健康 (Negative) | 假负例 (FN) (你猜错了,漏诊了病人) | 真负例 (TN) (你猜对了,他真健康) |
假设我们有一个模型,用来在100个人中筛查流感。
真实情况:实际上有10个人生病(P),90个人健康(N)。
模型预测结果 👇
- 模型预测了12个人生病。在这12个人里:
- 有8个是真的生病的(TP = 8)。
- 有4个是健康的,但被误判为生病(FP = 4)。
- 模型预测了88个人健康。在这88个人里:
- 有86个是真的健康的(TN = 86)。
- 有2个是生病的,但被漏掉了(FN = 2)。
我们的混淆矩阵就填好了:👇
| 预测 | 真实:生病 | 真实:健康 |
|---|---|---|
| 预测:生病 | TP = 8 | FP = 4 |
| 预测:健康 | FN = 2 | TN = 86 |
9.2 评估指标
光有表格还不够,我们需要一些具体的数字来衡量。
- 准确率 (Accuracy)
是什么: 猜对的总数占所有人数的比例。
公式: (TP + TN) / (TP + TN + FP + FN)
案例计算 :(8 + 86) / 100 = 94/100 = 94%
通俗理解 :“整体正确率”。这个模型100个人里猜对了94个,听起来很棒对吧?但别急,它有陷阱!
在数据不平衡时(比如99%是健康,1%是生病)会失灵(一个把所有人都预测为健康的模型,准确率也有99%,但毫无用处),漏掉了1%的病人,但它却认为“没事”。
2.精确率 (Precision)
是什么:在所有预测为生病的人中,真正生病的人的比例,关心的是“预测的准不准”。
公式 :TP / (TP + FP)
案例计算 :8 / (8 + 4) = 8/12 ≈ 66.7%
通俗理解 :宁缺毋滥 。衡量的是模型预测结果的“靠谱”程度。在这个案例中,模型说“你生病了”的结论,只有66.7%的可能是对的。这在某些场景(如垃圾邮件过滤)很重要,因为你不想总是把正常邮件误判为垃圾邮件(FP太高)。
- 召回率 (Recall)
是什么:在所有真正生病的人中,被模型成功找出来的比例,关心的是“找的全不全” 。
公式 :TP / (TP + FN)
案例计算 :8 / (8 + 2) = 8/10 = 80%
通俗理解 :“宁可错杀,不可放过”。衡量的是模型发现真正病人的“查全”能力。在这个案例中,10个真正的病人里,模型找出了8个,漏掉了2个。这在某些场景(如癌症筛查)极其重要,因为漏掉一个病人(FN)的代价非常高。
您会发现:精确率和召回率是矛盾的:提高一个,通常会降低另一个。
9.3 精确率和召回率的“调和”—— F度量 (F-Measure)
我们之前提到,精确率 (P) 和 召回率 (R) 经常是矛盾的,像一个跷跷板。
召回率:TP / (TP + FN)
精确率:TP / (TP + FP)
如果你想提高召回率(不漏掉一个病人),你就会倾向于“宁可错杀,不可放过”,把更多可疑的人都判断为生病(FP增加)。这会导致精确率下降(因为误诊的健康人变多了)。
如果你想提高精确率(确保你判断为生病的人一定是病人),你就会变得非常“保守”,只有证据非常充分时才判定为生病。这会导致召回率下降(因为很多真正的病人被漏掉了)。
那么问题来了: 如果一个模型的精确率是0.7,召回率是0.6;另一个模型的精确率是0.6,召回率是0.7。我们该选哪个?
这时候,我们需要一个单一的数字来综合衡量这两个指标。这就是F度量。
9.3.1 F度量
F1分数 是 精确率和召回率 的调和平均数。它给予较低的值更高的惩罚。
公式:F1 = 2 * (精确率 * 召回率) / (精确率 + 召回率)
也可以写成:F1 = (2 * TP) / (2 * TP + FP + FN)
F1分数能有效惩罚那些在精确率和召回率上表现极度不平衡的模型,迫使模型寻找一个平衡点。F1分数的取值范围是[0, 1],越接近1,模型综合性能越好。
9.3.2 Fβ分数:更通用的度量
有时候我们的任务就是更看重精确率或更看重召回率。比如:
短视频推荐系统:可能更看重精确率。因为推荐10个视频,用户有2个喜欢(精确率20%),也比推荐100个只有10个喜欢(精确率10%,但召回率可能更高)的体验要好。资源位是有限的。
癌症筛查: 可能更看重召回率。因为漏掉一个癌症病人(低召回率)的代价远高于让一个健康人做进一步检查(低精确率)。
这时,F1分数就不够灵活了,因为它认为精确率和召回率同等重要 。所以我们引入了更通用的 Fβ分数。
公式:Fβ = (1 + β²) * (精确率 * 召回率) / (β² * 精确率 + 召回率)
核心是 β 参数:
β > 1:表示召回率比精确率更重要。 例如,β=2 (F2分数),表示你重视召回率的程度是精确率的2倍。β < 1:表示精确率比召回率更重要。 例如,β=0.5 (F0.5分数),表示你重视精确率的程度是召回率的2倍(因为 1/β = 2)。β = 1:这就是我们熟悉的 F1分数,表示两者同等重要。
小结:👇
- F1分数是精确率和召回率的调和平均数,是综合评估分类模型的黄金标准之一,尤其适用于当我们对精确率和召回率没有特殊偏好的情况。
- Fβ分数是F1分数的灵活变体,通过β参数让我们可以根据具体业务需求,调整对精确率或召回率的偏好程度。
9.4 PR曲线和ROC曲线
之前我们讨论的精确率、召回率、F1分数都有一个前提:模型已经给出了一个确定的“是/否”的预测。
但实际上,很多分类模型(比如逻辑回归、神经网络)输出的是一个概率值 ,例如“这个病人有80%的概率生病”。我们需要设定一个阈值(Threshold),比如50%,才将这个概率转化为最终的分类决策(>50%判为生病,<50%判为健康)
PR曲线和ROC曲线 就是用来观察这个“阈值” 从高到低变化时,模型性能如何变化的“连续剧”,而不是一张“静态照片”。
9.4.1 PR曲线(精确率-召回率曲线)
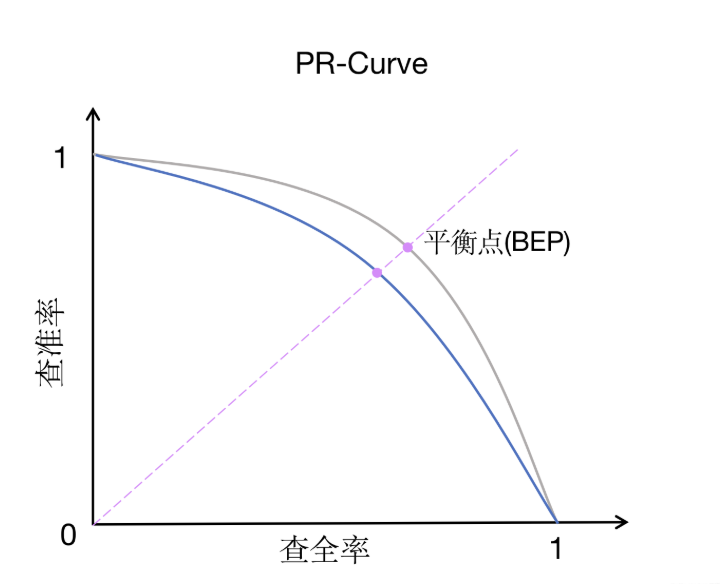
- 横轴是召回率 (Recall):代表“查全”的能力。
- 纵轴是精确率 (Precision):代表“查准”的能力。
- 曲线怎么画:我们将阈值从最高(1.0)逐步降到最低(0.0),每设定一个阈值,就计算出一对(召回率,精确率)的值,在图上点一个点。把所有点连起来,就形
- 理想模型 :曲线向右上角“凸”得越厉害越好。理想点是(1,1),即召回率和精确率都是100%。
- 现实模型 :曲线通常是一个从左上角(高精确率,低召回率)向右下角(低精确率,高召回率)滑落的曲线。
- 模型对比 :如果一个模型的PR曲线完全“包住”另一个模型的PR曲线,则前者性能更好。
- PR曲线下的面积(AUC-PR) :面积越大,模型综合性能越好。PR曲线特别适用于正样本(我们关心的类别,如“生病”)很少的“不平衡数据集”,因为它聚焦于正例的预测情况。
9.4.2 ROC曲线(接收者操作特征曲线)
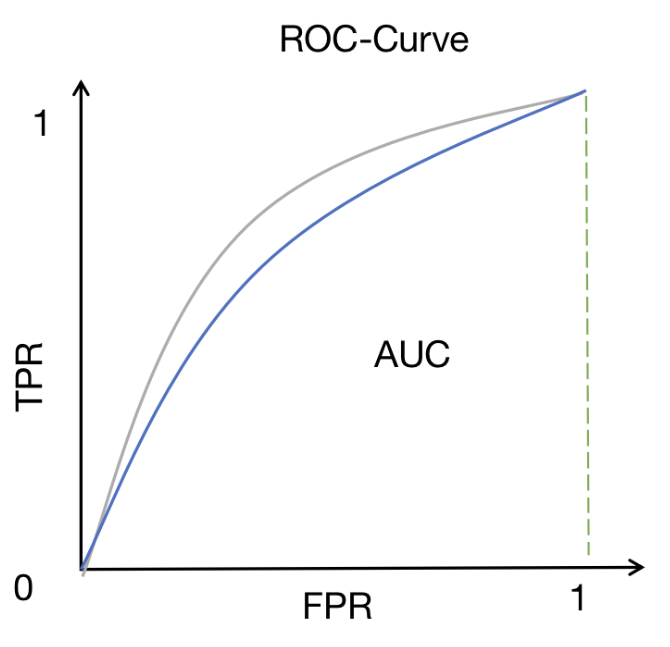
- 横轴是“假正率”(FPR) : FPR = FP / (FP + TN)。代表健康人被误判为生病的比例。我们希望它越小越好。
- 纵轴是“真正率”(TPR) ,也就是召回率(Recall): TPR = TP / (TP + FN)。代表病人被正确找出的比例。我们希望它越大越好。
- 曲线怎么画 :和PR曲线一样,通过不断改变阈值来获得多组 (FPR, TPR) 点,然后连线。
- 理想模型 :曲线向左上角“凸”得越厉害越好。理想点是(0,1),即FPR=0%(没有误诊),TPR=100%(全部找出)。
- 现实模型 :曲线越靠近左上角,说明模型在“尽量找出真病人”和“尽量不误诊健康人”之间权衡得越好。
- 模型对比 :同样,曲线越靠近左上角的模型性能越好。
- ROC曲线下的面积(AUC-ROC) :这是最常用的评估指标之一。
- AUC = 1:完美模型。
- AUC = 0.5:模型没有判别能力,和瞎猜一样。
- AUC > 0.5:模型优于随机猜测。AUC越接近1,模型性能越好。
9.5 模型选择 ---- 让模型变得更“通用”
问题一:过拟合 (Overfitting)
解决方法之一:正则化 (Regularization)
生活比喻:老师告诉学生:“不要只背答案,要理解核心公式和概念。一些特别偏、特别怪的解题技巧(可能只是巧合)不用花太多精力。”
- 是什么:在模型的学习过程中,我们给模型增加一个“惩罚项”,告诉它:“不要太复杂,尽量用简单的方式来解释数据。”
- 效果:限制了模型胡乱记忆训练数据中的噪声和细节,让它学到更本质、更通用的规律,从而在新数据上表现更好。
回顾下第六章学过的岭回归和LASSO,它们都是正则化模型。岭回归的惩罚项是:
λ * 模型参数的平方和。LASSO的惩罚项是:λ * 模型参数的绝对值和。
问题二:如何公平地评估模型?
解决方法:交叉验证 (Cross Validation)
通俗理解: 交叉验证充分利用了有限的数据,让每一份数据都既当过“学生”也当过“考官”,最终得到一个非常稳定、可靠的模型评估结果。
- 简单交叉验证
核心思想:最简单直接的方法,将数据集一次性分割成训练集和测试集。
- K折交叉验证
核心思想:将数据集分成K个大小相似的互斥子集,每次用K-1个子集训练,剩下的1个子集测试,重复K次。
- 留一交叉验证
核心思想:K折交叉验证的极端情况,其中K等于样本数量N。每次留下一个样本作为测试集,其余N-1个样本作为训练集。
| 方法 | 训练次数 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|---|
| 简单交叉验证 | 1 | 计算快,简单 | 结果不稳定,方差大 | 大数据集,快速原型 |
| K折交叉验证 | K | 结果稳定,偏差小 | 计算成本是K倍 | 中小数据集,模型选择 |
| 留一交叉验证 | N(样本数) | 几乎无偏,数据利用最大化 | 计算成本极高 | 小数据集,需要精确评估 |
选择建议:
- 对于大数据集 (>10,000样本):使用简单交叉验证或较小的K值(如5)
- 对于中小数据集 (100-10,000样本):使用K折交叉验证,K=5或10
- 对于小数据集 (<100样本):可以考虑留一交叉验证
- 在实际应用中,5折或10折交叉验证是最常用的平衡选择
案例代码
比较不同的交叉验证方法
1. 数据准备
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split, KFold, LeaveOneOut, cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report
import pandas as pd
import warnings
warnings.filterwarnings('ignore')
# 设置中文字体和图形样式
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
sns.set_style("whitegrid")
print("=== 交叉验证方法比较实验 ===\n")
# 创建模拟数据集
X, y = make_classification(n_samples=100, n_features=4, n_redundant=1,
n_informative=3, n_clusters_per_class=1,
random_state=42)
print("数据集形状:", X.shape)
print("类别分布:", np.bincount(y))
print("\n前5个样本的特征:")
print(X[:5])
print("\n对应的标签:")
print(y[:5])
# 创建DataFrame便于查看
df = pd.DataFrame(X, columns=[f'Feature_{i+1}' for i in range(X.shape[1])])
df['Target'] = y
print("\n数据集前5行:")
print(df.head())2. 可视化数据分布
# 数据可视化
fig, axes = plt.subplots(1, 2, figsize=(15, 5))
# 特征分布
for i in range(min(3, X.shape[1])):
axes[0].hist(X[y==0, i], alpha=0.7, label=f'Class 0 - Feature {i+1}')
axes[0].hist(X[y==1, i], alpha=0.7, label=f'Class 1 - Feature {i+1}')
axes[0].set_title('特征分布 by 类别')
axes[0].legend()
# 散点图显示两个主要特征
scatter = axes[1].scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', alpha=0.7)
axes[1].set_xlabel('Feature 1')
axes[1].set_ylabel('Feature 2')
axes[1].set_title('特征1 vs 特征2')
plt.colorbar(scatter, ax=axes[1])
plt.tight_layout()
plt.show()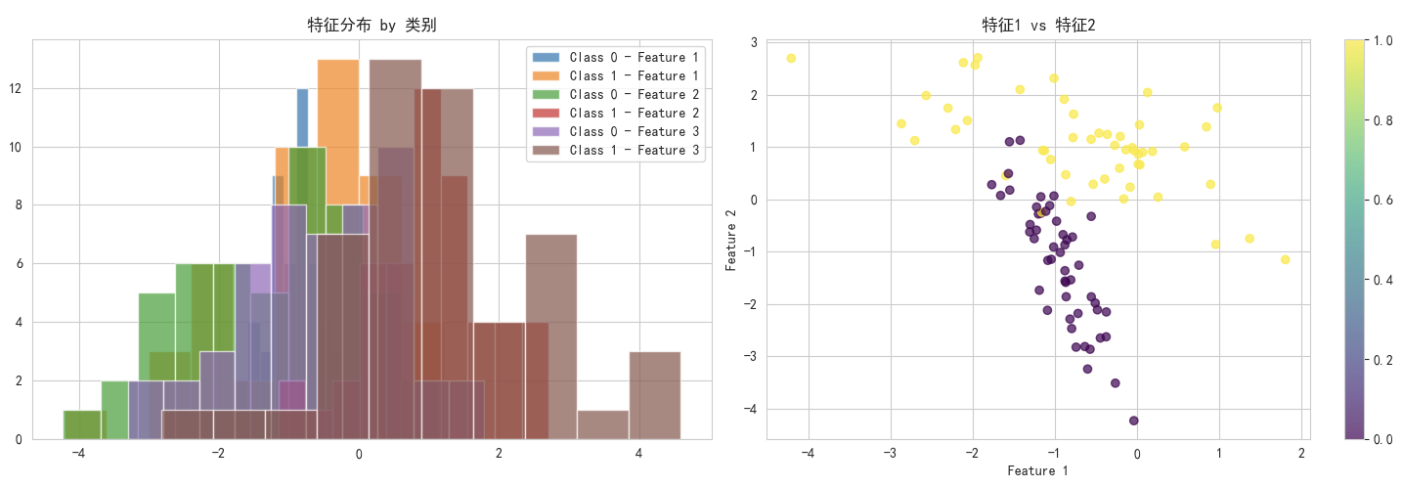
3. 简单交叉验证
print("\n" + "="*50)
print("1. 简单交叉验证(Hold-Out Validation)")
print("="*50)
# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
random_state=42, stratify=y)
print(f"训练集大小: {X_train.shape[0]} 个样本")
print(f"测试集大小: {X_test.shape[0]} 个样本")
print(f"训练集类别分布: {np.bincount(y_train)}")
print(f"测试集类别分布: {np.bincount(y_test)}")
# 训练模型
model_ho = LogisticRegression(random_state=42)
model_ho.fit(X_train, y_train)
# 预测并评估
y_pred_ho = model_ho.predict(X_test)
accuracy_ho = accuracy_score(y_test, y_pred_ho)
print(f"\n简单交叉验证准确率: {accuracy_ho:.4f}")
print("\n分类报告:")
print(classification_report(y_test, y_pred_ho))
# 可视化简单交叉验证结果
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap='coolwarm', alpha=0.6, s=50, label='真实标签')
plt.title('测试集 - 真实标签')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.subplot(1, 2, 2)
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_pred_ho, cmap='coolwarm', alpha=0.6, s=50, label='预测标签')
plt.title('测试集 - 预测标签')
plt.xlabel('Feature 1')
# 标记错误分类的点
errors = y_test != y_pred_ho
plt.scatter(X_test[errors, 0], X_test[errors, 1], facecolors='none', edgecolors='black', s=100, linewidth=2, label='错误分类')
plt.legend()
plt.tight_layout()
plt.show()
4. K折交叉验证
print("\n" + "="*50)
print("2. K折交叉验证(K-Fold Cross Validation)")
print("="*50)
# 设置不同的K值进行实验
k_values = [3, 5, 10]
kfold_results = {}
for k in k_values:
print(f"\n--- {k}-折交叉验证 ---")
kf = KFold(n_splits=k, shuffle=True, random_state=42)
model_kf = LogisticRegression(random_state=42)
# 进行交叉验证
cv_scores = cross_val_score(model_kf, X, y, cv=kf, scoring='accuracy')
kfold_results[k] = cv_scores
print(f"各折准确率: {[f'{score:.4f}' for score in cv_scores]}")
print(f"平均准确率: {cv_scores.mean():.4f} (+/- {cv_scores.std() * 2:.4f})")
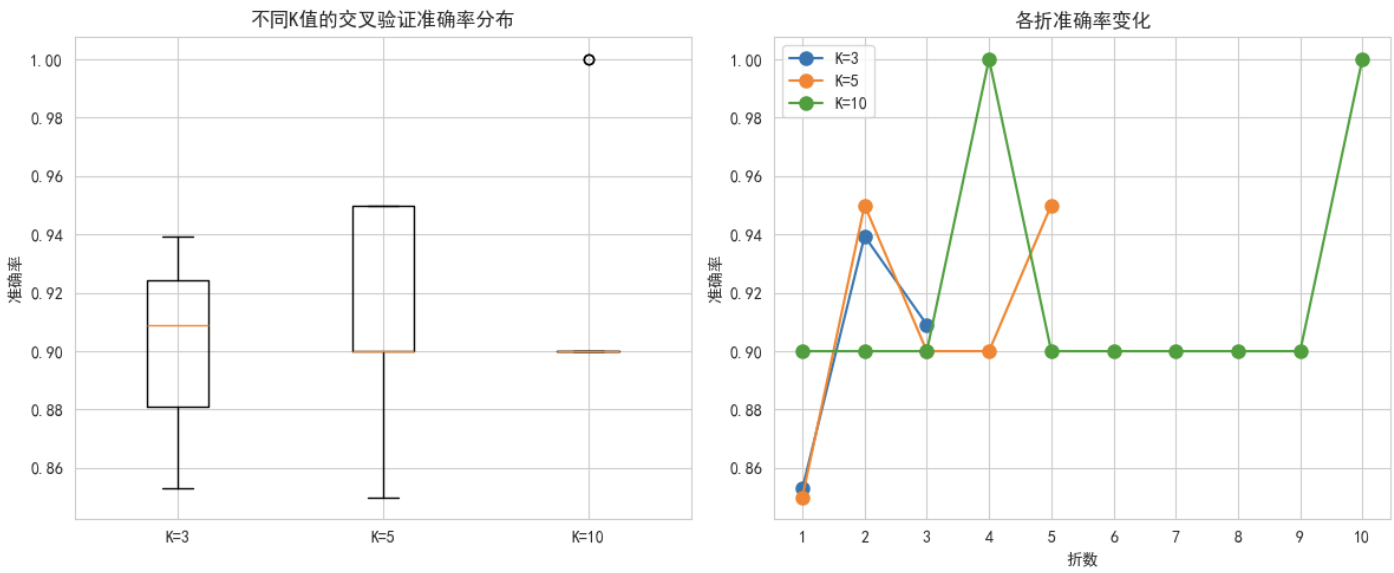
# 可视化K折交叉验证结果
plt.figure(figsize=(12, 5))
# 各折准确率箱线图
plt.subplot(1, 2, 1)
box_data = [kfold_results[k] for k in k_values]
plt.boxplot(box_data, labels=[f'K={k}' for k in k_values])
plt.title('不同K值的交叉验证准确率分布')
plt.ylabel('准确率')
# 各折准确率折线图
plt.subplot(1, 2, 2)
for k in k_values:
plt.plot(range(1, k+1), kfold_results[k], 'o-', label=f'K={k}', markersize=8)
plt.xlabel('折数')
plt.ylabel('准确率')
plt.title('各折准确率变化')
plt.legend()
plt.xticks(range(1, max(k_values)+1))
plt.tight_layout()
plt.show()
5. 留一交叉验证
print("\n" + "="*50)
print("3. 留一交叉验证(Leave-One-Out Cross Validation)")
print("="*50)
# 由于LOO计算量大,我们只演示原理和部分结果
print("留一法原理: 每次留一个样本作为测试集,其余作为训练集")
print(f"对于n={X.shape[0]}个样本,将进行{X.shape[0]}次训练和测试")
# 为了演示,我们只进行部分LOO验证
loo = LeaveOneOut()
model_loo = LogisticRegression(random_state=42)
# 只计算前20个样本的LOO验证,以节省时间
n_demo = min(20, X.shape[0])
scores_loo = []
print(f"\n演示前{n_demo}个样本的LOO验证:")
for i, (train_idx, test_idx) in enumerate(loo.split(X)):
if i >= n_demo:
break
X_train_loo, X_test_loo = X[train_idx], X[test_idx]
y_train_loo, y_test_loo = y[train_idx], y[test_idx]
model_loo.fit(X_train_loo, y_train_loo)
score = model_loo.score(X_test_loo, y_test_loo)
scores_loo.append(score)
if i < 5: # 只显示前5次的结果
print(f"样本 {test_idx[0]}: 真实标签={y_test_loo[0]}, 预测正确={score==1}")
# 使用cross_val_score计算完整的LOO准确率(平均值)
loo_mean_score = cross_val_score(LogisticRegression(random_state=42),
X, y, cv=LeaveOneOut()).mean()
print(f"\n留一法平均准确率: {loo_mean_score:.4f}")
print(f"演示的前{n_demo}个样本中,正确分类的比例: {np.mean(scores_loo):.4f}")
# 可视化LOO结果
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
correct_indices = [i for i, score in enumerate(scores_loo[:n_demo]) if score == 1]
wrong_indices = [i for i, score in enumerate(scores_loo[:n_demo]) if score == 0]
plt.bar(['正确分类', '错误分类'],
[len(correct_indices), len(wrong_indices)],
color=['green', 'red'])
plt.title(f'前{n_demo}个样本LOO验证结果')
plt.ylabel('样本数量')
plt.subplot(1, 2, 2)
plt.plot(range(1, n_demo+1), scores_loo, 'o-', markersize=6)
plt.axhline(y=loo_mean_score, color='r', linestyle='--', label=f'平均准确率: {loo_mean_score:.4f}')
plt.xlabel('样本序号')
plt.ylabel('分类结果 (1=正确, 0=错误)')
plt.title('各样本LOO验证结果')
plt.legend()
plt.tight_layout()
plt.show()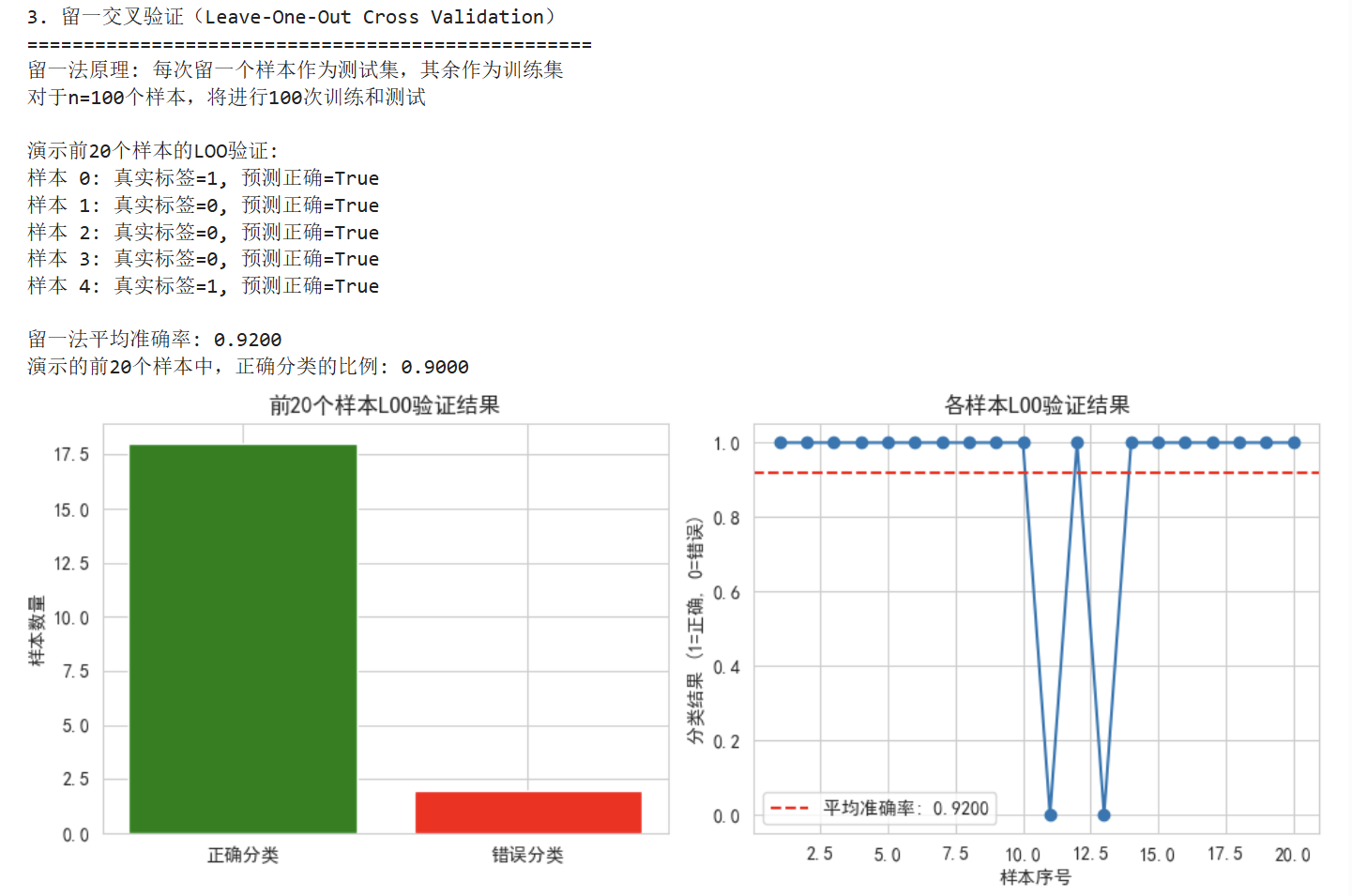
6. 方法比较与结果分析
print("\n" + "="*50)
print("4. 交叉验证方法比较")
print("="*50)
# 收集所有方法的准确率
comparison_data = {
'方法': ['简单交叉验证', '3折交叉验证', '5折交叉验证', '10折交叉验证', '留一法'],
'准确率': [
accuracy_ho,
kfold_results[3].mean(),
kfold_results[5].mean(),
kfold_results[10].mean(),
loo_mean_score
],
'标准差': [
0, # 简单交叉验证只有一次结果,无标准差
kfold_results[3].std(),
kfold_results[5].std(),
kfold_results[10].std(),
cross_val_score(LogisticRegression(random_state=42), X, y, cv=LeaveOneOut()).std()
],
'训练次数': [1, 3, 5, 10, X.shape[0]]
}
comparison_df = pd.DataFrame(comparison_data)
print("\n各方法性能比较:")
print(comparison_df)
# 可视化比较结果
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# 准确率比较
bars = axes[0, 0].bar(comparison_df['方法'], comparison_df['准确率'],
color=['blue', 'orange', 'green', 'red', 'purple'])
axes[0, 0].set_title('各方法准确率比较')
axes[0, 0].set_ylabel('准确率')
axes[0, 0].tick_params(axis='x', rotation=45)
# 在柱状图上添加数值
for bar, acc in zip(bars, comparison_df['准确率']):
height = bar.get_height()
axes[0, 0].text(bar.get_x() + bar.get_width()/2., height + 0.01,
f'{acc:.4f}', ha='center', va='bottom')
# 标准差比较(排除简单交叉验证)
methods_with_std = comparison_df[comparison_df['方法'] != '简单交叉验证']
axes[0, 1].bar(methods_with_std['方法'], methods_with_std['标准差'],
color=['orange', 'green', 'red', 'purple'])
axes[0, 1].set_title('各方法标准差比较(稳定性)')
axes[0, 1].set_ylabel('标准差')
axes[0, 1].tick_params(axis='x', rotation=45)
# 训练次数比较
axes[1, 0].bar(comparison_df['方法'], comparison_df['训练次数'],
color=['blue', 'orange', 'green', 'red', 'purple'])
axes[1, 0].set_title('各方法训练次数比较')
axes[1, 0].set_ylabel('训练次数')
axes[1, 0].tick_params(axis='x', rotation=45)
axes[1, 0].set_yscale('log') # 使用对数坐标因为LOO次数很大
# 准确率与训练次数的关系
axes[1, 1].scatter(comparison_df['训练次数'], comparison_df['准确率'], s=100)
for i, txt in enumerate(comparison_df['方法']):
axes[1, 1].annotate(txt, (comparison_df['训练次数'][i], comparison_df['准确率'][i]),
xytext=(10, 5), textcoords='offset points')
axes[1, 1].set_xlabel('训练次数')
axes[1, 1].set_ylabel('准确率')
axes[1, 1].set_title('准确率 vs 训练次数')
axes[1, 1].set_xscale('log')
plt.tight_layout()
plt.show()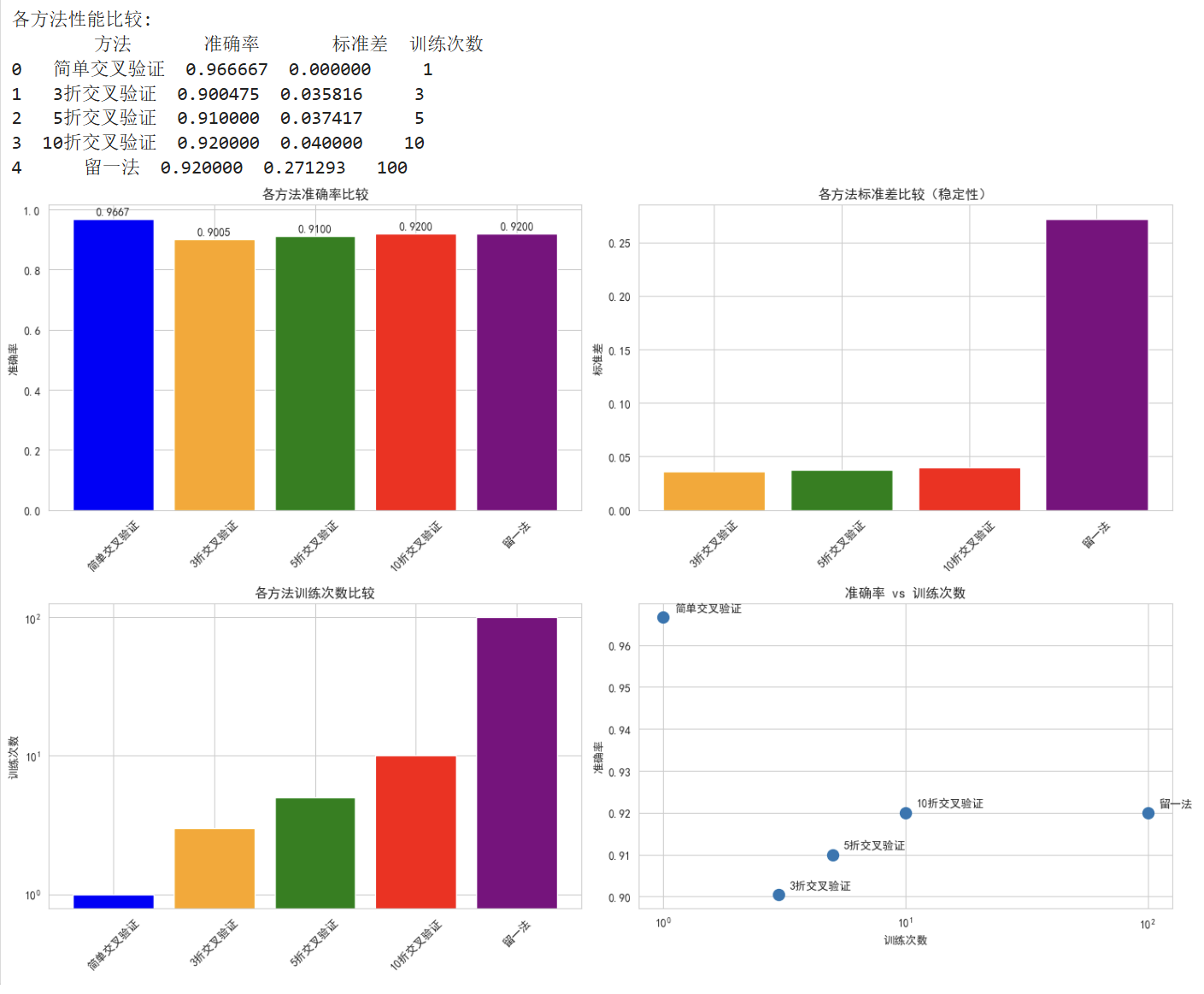
7. 结果解读:
简单交叉验证 (Hold-Out):
- 优点: 计算速度快,只训练一次模型
- 缺点: 结果受数据分割影响大,方差较高
- 适用: 大数据集,快速原型验证
K折交叉验证:
- 优点: 更好地利用数据,评估更稳定
- 缺点: 计算量是简单验证的K倍
- K值选择:
- K=3,5: 计算量适中,适合中等数据集
- K=10: 常用选择,在偏差和方差间取得平衡
留一法 (LOO):
- 优点: 最无偏的估计,几乎用尽所有数据
- 缺点: 计算量巨大(n次训练),方差可能较高
- 适用: 小数据集(n<1000)
🎯 实用建议:
- 数据量较大时 (>10,000样本): 使用简单交叉验证或5折交叉验证
- 数据量中等时 (1,000-10,000样本): 推荐10折交叉验证
- 数据量较小时 (<1,000样本): 考虑使用留一法或10折交叉验证
- 计算资源有限时: 优先选择5折或简单交叉验证
- 追求稳定评估时: 使用10折交叉验证,重复多次取平均
10. 模型组合分类
前言
1. 为什么要“组合”?—— 从个人英雄到团队作战
想象一下:你要解决一个复杂的问题,是找一个超级天才,还是找一个由普通人组成的优秀团队?
在机器学习中也是同样的道理!
单个分类器的问题: 👇
决策树:可能过于简单,像总用同一招式的拳手
复杂模型:可能过度学习,像死记硬背的学生
稳定性差:一次训练结果可能不理想
组合分类器的优势: 👇
“三个臭皮匠,顶个诸葛亮” —— 多个普通模型的组合往往胜过单个强大模型
2. 三种经典的“团队合作”策略
1️⃣ 策略一:袋装法 - 民主投票制
核心思想:创建多个相似的模型,让它们投票决定最终结果
#生活中的例子:医生会诊
#一个医生可能误诊,但多个医生独立诊断后投票,准确率更高!关键技术:自助采样法
- 从原始数据中有放回地随机抽取样本
- 每个模型看到的数据略有不同
- 最终结果由所有模型投票决定
2️⃣ 策略二:提升法 - 接力赛跑
核心思想:模型之间相互学习,后续模型专注于纠正前一个模型的错误
# 生活中的例子:学生做练习题
# 第一个学生做一遍 → 老师标记错误 → 第二个学生重点做错题 → 如此反复特点:
- 模型按顺序训练,而不是并行
- 每个新模型都“继承”前一个的经验教训
- 特别关注之前分错的样本
其中AdaBoost是提升法中最著名的代表,他的原理如下:
- 每个样本都有权重,开始都一样
- 分类器分错样本时,这些样本权重增加
- 准确率高的分类器在最终投票中话语权更大
3️⃣ 策略三:随机森林 - 专业化团队
**核心思想:**不仅随机选择数据,还随机选择特征,让每个模型各有专长
# 生活中的例子:医院各科室会诊
# 内科医生、外科医生、放射科医生...各有所长,共同诊断3. 实战案例:识别手写数字
让我们通过一个完整的例子来理解这些概念:
4.0. 数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier, AdaBoostClassifier, RandomForestClassifier
from sklearn.metrics import accuracy_score
# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
print("=== 手写数字识别:比较不同分类策略 ===\n")
# 1. 加载数据
digits = load_digits()
X, y = digits.data, digits.target
print(f"数据集信息:")
print(f"- 样本数量:{X.shape[0]}")
print(f"- 特征数量:{X.shape[1]} (8x8像素的图像)")
print(f"- 数字类别:0-9 共10个数字")
# 2. 可视化一些数字样本
plt.figure(figsize=(12, 4))
for i in range(10):
plt.subplot(2, 5, i+1)
plt.imshow(X[i].reshape(8, 8), cmap='gray')
plt.title(f"数字 {y[i]}")
plt.axis('off')
plt.tight_layout()
plt.show()
# 3. 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
random_state=42, stratify=y)
print(f"\n训练集:{X_train.shape[0]} 个样本")
print(f"测试集:{X_test.shape[0]} 个样本")
4.1 基准模型:单个决策树
print("\n" + "="*50)
print("1. 基准模型:单个决策树(个人英雄)")
print("="*50)
# 创建并训练单个决策树
single_tree = DecisionTreeClassifier(max_depth=10, random_state=42)
single_tree.fit(X_train, y_train)
# 预测并评估
y_pred_single = single_tree.predict(X_test)
accuracy_single = accuracy_score(y_test, y_pred_single)
print(f"单个决策树准确率:{accuracy_single:.4f}")
print("特点:简单直接,但可能不稳定")结果:👇
1. 基准模型:单个决策树(个人英雄)
==================================================
单个决策树准确率:0.8574
特点:简单直接,但可能不稳定4.2 袋装法:投票决策
print("\n" + "="*50)
print("2. 袋装法:民主投票制")
print("="*50)
# 创建袋装分类器(10个决策树)
bagging = BaggingClassifier(
estimator=DecisionTreeClassifier(max_depth=5),
n_estimators=10, # 10个模型
random_state=42
)
bagging.fit(X_train, y_train)
y_pred_bagging = bagging.predict(X_test)
accuracy_bagging = accuracy_score(y_test, y_pred_bagging)
print(f"袋装法准确率:{accuracy_bagging:.4f}")
print(f"提升效果:{accuracy_bagging - accuracy_single:+.4f}")
# 查看每个基分类器的表现
print("\n各个基分类器的准确率:")
for i, estimator in enumerate(bagging.estimators_):
acc = estimator.score(X_test, y_test)
print(f"分类器 {i+1}: {acc:.4f}")结果👇
==================================================
2. 袋装法:民主投票制
==================================================
袋装法准确率:0.8407
提升效果:-0.0167
各个基分类器的准确率:
分类器 1: 0.6907
分类器 2: 0.6444
分类器 3: 0.7407
分类器 4: 0.6519
分类器 5: 0.6722
分类器 6: 0.6389
分类器 7: 0.7130
分类器 8: 0.6870
分类器 9: 0.7148
分类器 10: 0.71854.3 AdaBoost:接力学习
print("\n" + "="*50)
print("4. AdaBoost:接力学习")
print("="*50)
# 创建AdaBoost分类器
adaboost = AdaBoostClassifier(
estimator=DecisionTreeClassifier(max_depth=3),
n_estimators=10, # 10个分类器
learning_rate=0.8, # 学习率
random_state=42
)
adaboost.fit(X_train, y_train)
y_pred_ada = adaboost.predict(X_test)
accuracy_ada = accuracy_score(y_test, y_pred_ada)
print(f"AdaBoost准确率:{accuracy_ada:.4f}")
print(f"提升效果:{accuracy_ada - accuracy_single:+.4f}")
# 查看每个分类器的权重
print("\n各个分类器的权重(话语权):")
for i, weight in enumerate(adaboost.estimator_weights_):
print(f"分类器 {i+1} 的权重: {weight:.4f}")结果👇
==================================================
3. AdaBoost:接力学习
==================================================
AdaBoost准确率:0.8389
提升效果:-0.0185
各个分类器的权重(话语权):
分类器 1 的权重: 1.7336
分类器 2 的权重: 2.4483
分类器 3 的权重: 1.9778
分类器 4 的权重: 2.1041
分类器 5 的权重: 1.6423
分类器 6 的权重: 2.2030
分类器 7 的权重: 1.8306
分类器 8 的权重: 2.0610
分类器 9 的权重: 2.0506
分类器 10 的权重: 1.81444.4 随机森林:专业化团队
print("\n" + "="*50)
print("3. 随机森林:专业化团队")
print("="*50)
# 创建随机森林
random_forest = RandomForestClassifier(
n_estimators=10, # 10棵树
max_depth=5, # 每棵树的深度
random_state=42
)
random_forest.fit(X_train, y_train)
y_pred_rf = random_forest.predict(X_test)
accuracy_rf = accuracy_score(y_test, y_pred_rf)
print(f"随机森林准确率:{accuracy_rf:.4f}")
print(f"提升效果:{accuracy_rf - accuracy_single:+.4f}")
# 特征重要性分析
print("\n前5个最重要的特征(像素):")
feature_importance = random_forest.feature_importances_
top5_indices = np.argsort(feature_importance)[-5:][::-1]
for i, idx in enumerate(top5_indices):
row, col = idx // 8, idx % 8
print(f"第{i+1}重要: 位置({row}, {col}), 重要性: {feature_importance[idx]:.4f}")结果👇
==================================================
4. 随机森林:专业化团队
==================================================
随机森林准确率:0.8648
提升效果:+0.0074
前5个最重要的特征(像素):
第1重要: 位置(2, 5), 重要性: 0.0652
第2重要: 位置(3, 4), 重要性: 0.0598
第3重要: 位置(5, 3), 重要性: 0.0506
第4重要: 位置(4, 1), 重要性: 0.0490
第5重要: 位置(7, 2), 重要性: 0.04424.5 结果比较与可视化
# 比较所有方法
methods = ['单个决策树', '袋装法', '随机森林', 'AdaBoost']
accuracies = [accuracy_single, accuracy_bagging, accuracy_rf, accuracy_ada]
colors = ['lightblue', 'lightgreen', 'lightcoral', 'gold']
plt.figure(figsize=(12, 5))
# 准确率比较
plt.subplot(1, 2, 1)
bars = plt.bar(methods, accuracies, color=colors, edgecolor='black')
plt.ylabel('准确率')
plt.title('不同分类策略的性能比较')
plt.ylim(0.7, 1.0)
# 在柱子上添加数值
for bar, acc in zip(bars, accuracies):
height = bar.get_height()
plt.text(bar.get_x() + bar.get_width()/2., height + 0.01,
f'{acc:.4f}', ha='center', va='bottom')
# 提升效果比较
plt.subplot(1, 2, 2)
improvements = [0, accuracy_bagging-accuracy_single,
accuracy_rf-accuracy_single, accuracy_ada-accuracy_single]
plt.bar(methods, improvements, color=colors, edgecolor='black')
plt.ylabel('相对于基准的提升')
plt.title('组合方法带来的提升效果')
plt.axhline(y=0, color='black', linestyle='-', alpha=0.3)
plt.tight_layout()
plt.show()
print("\n" + "="*60)
print("实验总结与分析")
print("="*60)
4.6. 深入理解:错误分析
# 分析哪些数字容易被误判
from sklearn.metrics import confusion_matrix
import seaborn as sns
# 选择最佳模型进行分析
best_model = random_forest # 以随机森林为例
y_pred_best = best_model.predict(X_test)
cm = confusion_matrix(y_test, y_pred_best)
plt.figure(figsize=(10, 8))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',
xticklabels=range(10), yticklabels=range(10))
plt.xlabel('预测标签')
plt.ylabel('真实标签')
plt.title('混淆矩阵 - 识别错误分析')
plt.show()
print("\n错误分析:")
print("对角线上的数字表示正确分类的数量")
print("非对角线上的数字表示误分类的情况")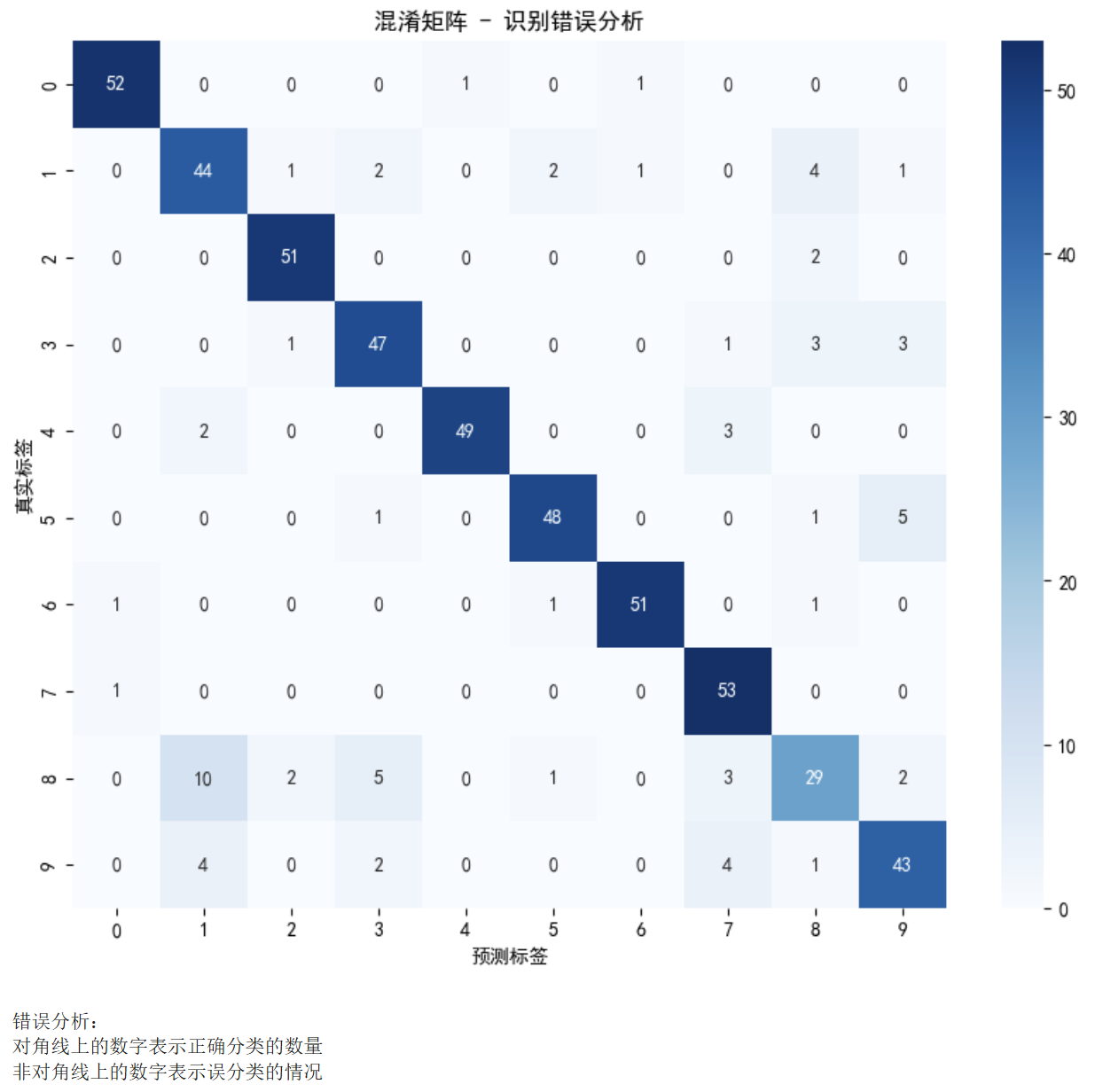
记住:没有最好的算法,只有最适合问题的算法!
