数据仓库与数据挖掘第七章

yange大约 30 分钟大数据学科数仓

1.关联规则分析概述

关联规则分析概述

定义

关联规则

我们每天都在接收大量的信息，其中有些信息是相互关联的，那么如何分析他们之间的相关性呢？

在统计学中，有一个指标叫相关系数。
在信息论里，有一种工具叫互信息。
在数据挖掘中，有一种算法叫关联规则。

在不同的场景中，应用的方法不一样，但目标都是对相关性进行量化分析。需要注意的是，相关关系通常不是因果关系，即使是因果关系，也要搞清楚：谁是原因？谁是结果？千万不能颠倒因果关系的顺序。

比如说，有人认为，因为比尔·盖茨退学，所以创业取得了成功。但事实却是，比尔·盖茨先是证明了自己初期的创业已经成功了，然后才退学的。一些媒体为了吸引眼球，故意颠倒因果关系，怂恿大学生退学去创业，其实害人不浅。假如我们去统计大量的退学创业案例，把创业成功这件事看成一个随机事件 X，把退学这件事看成另一个随机事件 Y，就会发现它们的相关性几乎为零。

关联规则数据挖掘，最经典的案例就是沃尔玛的啤酒和尿布的故事。沃尔玛拥有世界上最大的数据仓库系统，为了能够准确了解顾客在其门店的购买习惯，沃尔玛对其顾客的购物行为进行购物篮分析，想知道顾客经常一起购买的商品有哪些。沃尔玛数据仓库里集中了其各门店的详细原始交易数据。在这些原始交易数据的基础上，沃尔玛利用数据挖掘方法对这些数据进行分析和挖掘。一个意外的发现是：“跟尿布一起购买最多的商品竟是啤酒！”经过大量实际调查和分析，揭示了一个隐藏在“尿布与啤酒”背后的一种行为模式：在美国，一些年轻的父亲下班后经常要到超市去买婴儿尿布，而他们中有 30% ～ 40% 的人同时也为自己买一些啤酒。产生这一现象的原因是：美国的太太们常叮嘱她们的丈夫下班后为小孩买尿布，而丈夫们在买尿布后又随手带回了他们喜欢的啤酒。关联规则通常会涉及到几个重要的参数，如项集、支持度、置信度、提升度等。

一、关联规则挖掘的基本元素

案例数据集：某超市1周内的 5条购物篮事务记录（简化版“啤酒与尿布”数据），如表 7-1所示。

事务ID（TID）	购买的商品（项集）
T1	`{牛奶, 面包, 尿布}`
T2	`{啤酒, 尿布, 面包, 可乐}`
T3	`{牛奶, 尿布, 啤酒}`
T4	`{面包, 牛奶, 尿布, 啤酒}`
T5	`{尿布, 牛奶, 可乐}`

1️⃣ 1 . 事务（Transaction）
定义：一次完整的购买行为记录（一行数据）。
案例：T2是一条事务，内容为{啤酒, 尿布, 面包, 可乐}。

2️⃣ 2. 项（Item）
定义：事务中的最小商品单元。
案例：牛奶、啤酒、尿布、面包、可乐（共5个项）。

3️⃣ 3. 项集（Itemset）

定义：由多个项组成的集合，按项数分为k-项集（k=1,2,...）。
案例：
- 1-项集：{啤酒}、{尿布}（单个商品）；
- 2-项集：{啤酒, 尿布}（两个商品组合）；
- 3-项集：{啤酒, 尿布, 牛奶}（三个商品组合）。

二、核心评价指标

目标：用案例数据计算支持度、置信度、提升度，理解其业务含义。

4️⃣ 支持度（Support）：“这个商品组合常见吗？”

定义：项集在所有事务中出现的频率（概率）。
公式：Support(X) = 包含X的所有事务数 / 总事务数

案例计算：
项集{啤酒}的支持度：
→ 包含{啤酒}的事务：T2、T3、T4（共3条）；
→ Support({啤酒})=3/5=60%（5条事务中，60%的人买了啤酒）。

项集{啤酒, 尿布}的支持度：
→ 包含{啤酒, 尿布}的事务：T2、T3、T4（共3条）；
→ Support({啤酒,尿布})=3/5=60%（60%的人同时买了啤酒和尿布）。

5️⃣ 置信度（Confidence）：“买了A就会买B吗？”

定义：规则X→Y 的可信程度（买了X的人，有多大比例买了Y）。
公式：Confidence(X→Y) = Support(X∪Y) / Support(X)。

案例计算：
规则{啤酒}→{尿布}的置信度： 👇
Support({啤酒,尿布})=60%，
Support({啤酒})=60%；
Confidence({啤酒}→{尿布})=60%/60%=100%（买了啤酒的人，100%也买了尿布！）。

规则{尿布}→{啤酒}的置信度：
→ 包含{尿布}的事务：T1~T5（共5条，所有事务都买了尿布）；
→ Support({尿布})=5/5=100%；
→ Confidence({尿布}→{啤酒})=60%/100%=60%（买了尿布的人，60%会买啤酒）。

6️⃣ 提升度（Lift）：“买A真的会促进买B吗？”

问题：{尿布}→{啤酒}的置信度60%，但尿布本身是“必买品”（支持度100%），这个规则有意义吗？
定义：衡量规则 X→Y 的“实际关联强度”，即X的出现是否真的提升了Y的出现概率。
公式：
Lift(X→Y)=Support(Y) / Support(X∪Y)
Confidence(X→Y)=Support(X∪Y) / Support(X)
Lift(X→Y)=Support(Y) / Confidence(X→Y)

理论区间：
(0,+∞)，核心关注 Lift>1 的正向关联。
业务阈值：

入门筛选：min_lift=1（排除负关联）；
实用筛选：min_lift=1.2~2（平衡关联强度与普遍性）；
强规则筛选：min_lift≥3（聚焦高价值模式）。

案例计算：
规则{啤酒}→{尿布}的提升度：
Support(Y=尿布)=5/5=100%；
Confidence(X→Y)=60%/60%=100%；
Lift=100%/100%=1.0（买啤酒对买尿布的概率无提升，因尿布本身100%被购买）。

规则{啤酒}→{牛奶}的提升度：
Support({啤酒,牛奶})=2/5=40%（T3、T4包含啤酒和牛奶）；
Support({啤酒})=60%，
Support({牛奶})=4/5=80%；
Confidence({啤酒}→{牛奶})=40%/60%≈66.7%；
Lift=66.7%/80%≈0.83<1（买啤酒会降低买牛奶的概率，负关联）。

关键案例：{面包}→{牛奶}的提升度：
Support({面包,牛奶})=3/5=60%（T1、T4、T5）；
Support({面包})=4/5=80%，
Support({牛奶})=80%；
Confidence=60%/80%=75%；
Lift=75%/80%≈0.94<1（伪关联：面包和牛奶均高频，但无实际关联）。

有价值的规则：{可乐}→{面包}：
Support({可乐,面包})=2/5=40%（T2、T5）；
Support({可乐})=2/5=40%，
Support({面包})=80%；
Confidence=40%/40%=100%；
Lift=100%/80%=1.25>1（买可乐的人100%买面包，且比随机买面包的概率提升25%，是真关联）。

规则	支持度	置信度	提升度	业务含义总结
`{啤酒}→{尿布}`	60%	100%	1.0	常见且可靠（买啤酒的人100%买尿布），但因尿布本身100%被购买，规则无实际促销价值（Lift=1，无提升）。
`{可乐}→{面包}`	40%	100%	1.25	较常见且高度可靠（买可乐的人100%买面包），且买可乐对买面包的概率有25%提升（Lift>1），可用于捆绑促销。
`{啤酒}→{牛奶}`	40%	66.7%	0.83	较常见但可靠性一般，且买啤酒会降低买牛奶的概率（Lift<1，负关联），无业务价值。
`{面包}→{牛奶}`	60%	75%	0.94	支持度和置信度均较高，但因两者均为高频商品，实际无关联（Lift≈1，伪关联），无需重点关注。

总结：

支持度：筛选“常见”的商品组合（如支持度≥40%，避免挖掘小众组合）；
置信度：筛选“可靠”的规则（如置信度≥60%，确保买A后大概率买B）；
提升度：筛选“有实际关联”的规则（Lift>1，排除伪关联，如高频商品的偶然共存）。

2.频繁项集挖掘方法

数据仓库概要

定义

好的，我们继续深入👍。同学们已经透彻地理解了关联规则的核心概念（支持度、置信度、提升度）和它们背后的业务意义。

现在，我们面临一个现实问题： 如何从海量的交易数据中，高效地找出所有满足最小支持度阈值的项集？ ❔

这就是 Apriori算法要解决的核心问题。它是最经典、最著名的关联规则挖掘算法，其名称源于它使用了一个先验知识：如果一个项集是频繁的，那么它的所有子集也一定是频繁的。

一、为什么需要Apriori？
想象一个超市有10,000种商品（项）。

要找出所有1-项集（单个商品），只有10,000种可能。
要找出所有2-项集（商品对），组合数将高达约5千万 (C(10000,2))。
要找出所有3-项集，组合数将是约1660亿 (C(10000,3))。
如果我们暴力地计算每一个可能的项集的支持度，计算量将是天文数字，完全不可行。Apriori算法通过巧妙的剪枝策略，极大地减少了需要考察的项集数量。

二、Apriori算法的核心思想：两步过程 & 逐层搜索

Apriori原理（关键）：如果一个项集不是频繁的，那么它的所有超集也绝不可能是频繁的。

这是一个逆向思维：👇

既然频繁项集的所有子集必须频繁，那么只要某个子集不频繁，我们就完全可以忽略所有包含它的更大集合，因为它们注定不满足支持度要求。

基本步骤：👇
（1）扫描全部数据，产生候选1-项集的集合C1；
（2）根据最小支持度，由候选1-项集的集合C1 ---> 产生 ---> 频繁1-项集的集合L；
（3）对k>1，重复执行步骤（4）、（5）、（6）；
（4）由Lk执行连接和剪枝操作，---> 产生 ---> 候选（k+1）-项集的集合C（k+1）。
（5）根据最小支持度，由候选（k+1）-项集的集合C（k+1），---> 产生 ---> 频繁（k+1）-项集的集合L（k+1）；
（6）若L≠Ф，则k=k+1，跳往步骤（4）；否则往下执行；
（7）根据最小置信度，由频繁项集产生强关联规则，程序结束。

三、案例实战：用Apriori算法挖掘频繁项集
让我们回到您提供的超市数据集，设定最小支持度（min_support）为 40%（即出现次数 >= 2次）。

事务数据库 (Database D):

TID	商品 (Items)
T1	`{牛奶, 面包, 尿布}`
T2	`{啤酒, 尿布, 面包, 可乐}`
T3	`{牛奶, 尿布, 啤酒}`
T4	`{面包, 牛奶, 尿布, 啤酒}`
T5	`{尿布, 牛奶, 可乐}`

第1轮迭代：发现频繁1-项集 (L₁)

扫描数据库，计算所有1-项集的支持度计数。

候选1-项集 (C₁)	出现的事务	支持度计数	是否频繁？(≥2)
`{牛奶}`	T1,T3,T4,T5	4	✅是
`{面包}`	T1,T2,T4	4	✅是
`{尿布}`	T1,T2,T3,T4,T5	5	✅是
`{啤酒}`	T2,T3,T4	3	✅是
`{可乐}`	T2,T5	2	✅是

结果： 频繁1-项集 L₁ = { {牛奶}, {面包}, {尿布}, {啤酒}, {可乐} }

第2轮迭代：发现频繁2-项集 (L₂)

连接步 (Join): 将L₁中的项两两连接，生成候选2-项集 C₂。
C₂ = { {牛奶,面包}, {牛奶,尿布}, {牛奶,啤酒}, {牛奶,可乐}, {面包,尿布}, {面包,啤酒}, {面包,可乐}, {尿布,啤酒}, {尿布,可乐}, {啤酒,可乐} }
剪枝步 (Prune): 基于Apriori原理，C₂中所有候选的1项子集都在L₁中，无需剪枝。

剪枝步：检查C₂中每个候选的所有2项子集是否都在L₁中。
例如：检查{牛奶,面包}的所有2项子集{牛奶}、{面包}是否都在L₁中。
如果都不在L₁中，则剪枝（删除）该候选。

扫描数据库，计算C₂中每个项集的支持度计数。

候选2-项集 (C₂)	出现的事务	支持度计数	是否频繁？(≥2)
`{牛奶,面包}`	T1, T4	3	✅是
`{牛奶,尿布}`	T1,T3,T4,T5	4	✅是
`{牛奶,啤酒}`	T3, T4	2	✅是
`{牛奶,可乐}`	T5	1	❌否
`{面包,尿布}`	T1,T2,T4	3	✅是
`{面包,啤酒}`	T2, T4	2	✅是
`{面包,可乐}`	T2	1	❌否
`{尿布,啤酒}`	T2,T3,T4	3	✅是
`{尿布,可乐}`	T2, T5	2	✅是
`{啤酒,可乐}`	T2	1	❌否

结果： 频繁2-项集 L₂ = { {牛奶,面包}, {牛奶,尿布}, {牛奶,啤酒}, {面包,尿布}, {面包,啤酒}, {尿布,啤酒}, {尿布,可乐} }

第3轮迭代：发现频繁3-项集 (L₃)

连接步 (Join): 将L₂中的项集连接生成候选3-项集 C₃。
- 连接方式：两个项集的前(k-1)个项相同，最后一项不同。
- 例如：连接 {牛奶,面包} 和 {牛奶,尿布} → {牛奶,面包,尿布}
- 例如：连接{牛奶,尿布}和 {牛奶,啤酒} → {牛奶,尿布,啤酒}
- 例如：连接 {面包,尿布} 和 {面包,啤酒} → {面包,尿布,啤酒}
- 例如：连接 {尿布,啤酒} 和 {尿布,可乐} → {啤酒,尿布,可乐}
C₃ = { {牛奶,面包,尿布}, {牛奶,尿布,啤酒}, {面包,尿布,啤酒}, {牛奶,尿布,可乐}, {面包,尿布,可乐}, {啤酒,尿布,可乐} }
剪枝步 (Prune): 应用Apriori原理，检查C₃中每个候选的所有2项子集是否都在L₂中。
- {牛奶,面包,尿布}: 子集 {牛奶,面包}∈L₂, {牛奶,尿布}∈L₂, {面包,尿布}∈L₂ → 保留
- {牛奶,尿布,啤酒}: 子集 {牛奶,尿布}∈L₂, {牛奶,啤酒}∈L₂, {尿布,啤酒}∈L₂ → 保留
- {面包,尿布,啤酒}: 子集 {面包,尿布}∈L₂, {面包,啤酒}∈L₂, {尿布,啤酒}∈L₂ → 保留
- {牛奶,尿布,可乐}: 子集 {牛奶,尿布}∈L₂, {牛奶,可乐}∉L₂, {尿布,可乐}∈L₂ → ❌剪枝 (因为{牛奶,可乐}不在L₂中)
- {面包,尿布,可乐}: 子集 {面包,尿布}∈L₂, {面包,可乐}∉L₂, {尿布,可乐}∈L₂ → ❌剪枝 (因为{面包,可乐}不在L₂中)
- {啤酒,尿布,可乐}: 子集 {尿布,啤酒}∈L₂, {尿布,可乐}∈L₂, {啤酒,可乐}∉L₂ → ❌剪枝 (因为{啤酒,可乐}不在L₂中)
经剪枝后，需计算的C₃ = { {牛奶,面包,尿布}, {牛奶,尿布,啤酒}, {面包,尿布,啤酒} }
扫描数据库，计算上述候选的支持度计数。

候选3-项集 (C₃)	出现的事务	支持度计数	是否频繁？(≥2)
`{牛奶,面包,尿布}`	T1, T4	2	✅是
`{牛奶,尿布,啤酒}`	T3, T4	2	✅是
`{面包,尿布,啤酒}`	T2, T4	2	✅是

结果： 频繁3-项集 L₃ = { {牛奶,面包,尿布}, {牛奶,尿布,啤酒}, {面包,尿布,啤酒} }

第4轮迭代：尝试发现频繁4-项集 (L₄)

连接步 (Join): 连接L₃中的项集。L₃中项集的前两个项各不相同，无法进行有效的连接（连接要求前k-1项相同）。例如：
- {牛奶,面包,尿布} 和 {牛奶,尿布,啤酒} 的前两项(牛奶,面包) vs (牛奶,尿布) 不同，无法连接。
- 无法生成任何候选4-项集。
- 假如L₃中项集的前两项相同，则可以进行有效的连接。比如：
- {牛奶,面包,尿布} 和 {牛奶,面包,啤酒} 的前两项(牛奶,面包) vs (牛奶,面包) 相同，可以连接。
- 生成候选4-项集 {牛奶,面包,尿布,啤酒}

算法终止。

最终，我们找到了所有频繁项集：

L₁: { {牛奶}, {面包}, {尿布}, {啤酒}, {可乐} }
L₂: { {牛奶,面包}, {牛奶,尿布}, {牛奶,啤酒}, {面包,尿布}, {面包,啤酒}, {尿布,啤酒}, {尿布,可乐} }
L₃: { {牛奶,面包,尿布}, {牛奶,尿布,啤酒}, {面包,尿布,啤酒} }

👇 👇

L₁（塔基）: 代表所有畅销单品。了解哪些商品是流量之王。
L₂（塔身）: 代表所有强力的两两组合。这是行动的“主战场”，用于大多数推荐和营销策略。
L₃及更高阶（塔尖）: 代表最复杂的群体行为模式。用于发现一些意想不到的、更深层次的关联，指导套餐设计和战略布局。

3.提高Apriori算法效率

提高Apriori算法效率

定义

3.1 提高Apriori算法效率的方式

Apriori算法效率低下的主要根源在于：

多次扫描数据库：每次计算候选项集的支持度都需要遍历整个数据库，I/O开销巨大。
巨大的候选项集数量：尤其是当频繁1项集L₁很大时，生成的候选项集C_k会呈指数级增长，C₂的数量级就是O(n²)。
昂贵的支持度计数：需要将每个候选项集与每个交易记录进行比较，计算量非常大。

解决方案：👇
1️⃣ 基于散列的技术（Hashing）
方法：
在生成候选项集C₂时，使用一个散列函数将项集映射到散列表的各个桶中。一个交易记录中的所有2项子集都会被散列到对应的桶中并增加桶的计数。
如何提升效率：
在后续计算支持度时，如果一个候选项集的对应桶的计数低于最小支持度阈值，那么无需扫描数据库就可以直接确定这个候选项集是非频繁的，可以将其从C₂中剪枝掉。这能有效减少需要检查的候选项集数量。
例子：
比如有{A,B}和{A,C}两个项集，它们可能被散列到同一个桶。如果这个桶的总计数都小于最小支持度，那么这两个项集都可以被提前剪枝。

2️⃣ 事务压缩（Transaction Reduction）
方法：
不包含任何Lₖ中项集的交易记录在后续的扫描中不再参与支持度计数，因为它们不可能对生成更高阶的频繁项集有任何贡献。

如何提升效率：
随着k的增加，有效数据库的大小会逐渐减小，减少了需要扫描的记录数量。

例子：
如果一个交易记录包含Lₖ中的项集，那么这个交易记录的所有2项子集都会被包含在C_(k+1)中。因此，这个交易记录在后续的扫描中可以不再参与计算，从而减少计算量。

3️⃣采样（Sampling）
方法：
从原始数据库中抽取一个随机样本，在样本上使用Apriori算法来寻找频繁项集。
挑战：
可能会产生伪频繁项集（在样本中频繁但在整体中不频繁）和漏掉一些真正的频繁项集。
如何提升效率：
通过一次扫描得到样本，后续计算都在内存中的样本上进行，速度极快。通常需要一次额外的数据库扫描来验证结果的有效性。

4️⃣ 动态项集计数（Dynamic Itemset Counting, DIC）
方法：
在数据库扫描过程中，一旦某个候选项集的支持度计数已经确定达到最小支持度，就立即将其标记为频繁项集，而不用等到扫描结束。同时，可以立即基于这个新发现的频繁项集生成新的候选项集。
如何提升效率：
它采用了类似“流水线”的方式，允许在一次数据库扫描中交错进行不同大小k的项集的支持度计数，有可能在更少的扫描次数内找到所有频繁项集。

3.2 频繁模式增长算法-FP-Growth

FP-Growth 它是一种非常高效且广泛使用的算法，用于从数据集中挖掘频繁项集（即经常一起出现的物品集合），而 无需生成候选项集 。它完美地解决了Apriori算法的主要性能瓶颈。

核心思想：用空间换时间，避免生成候选项集

Apriori算法的低效主要源于需要反复扫描数据库来验证海量的候选项集的支持度。

FP-Growth算法的天才之处在于：👍
将整个数据库压缩成一棵紧凑的数据结构——FP树（Frequent-Pattern Tree）。这棵树保留了项集之间的关联信息。
通过递归地“生长”这棵树来挖掘频繁模式，整个过程在内存中进行，无需多次扫描原始数据库，也完全避免了生成候选项集。

接下来我们使用上面Apriori的演示案例的原始数据集，来演示FP-Growth算法的运行过程。

一、步骤1：频繁1-项集及事务重排

目标：筛选频繁项并按支持度排序，重排事务数据。

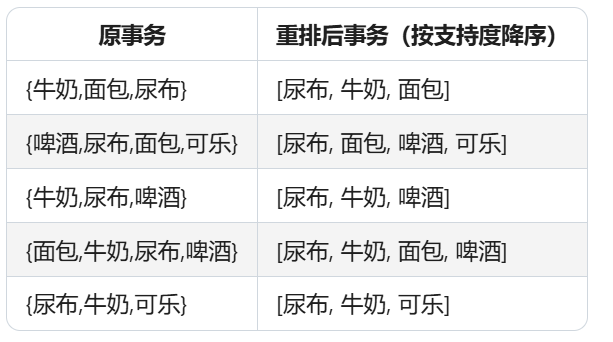
频繁1-项集（支持度≥2，按降序排序）：

  尿布(5) > 牛奶(4) > 面包(3) > 啤酒(3) > 可乐(2)  （支持度相同的项按字母序排序，如面包和啤酒）

事务数据重排（仅保留频繁项，按上述顺序排序）：

二、步骤2：构建FP树（核心步骤）

FP树结构：根节点（null）+ 项节点（含支持度、父/子指针）+ 头指针表（记录每项的节点链表）。
构建过程：逐条插入重排后的事务，更新节点支持度和指针。

最终FP树图形（简化版，节点格式：项名(支持度)）：

          根节点(null)
             │
             ▼
          尿布(5)  <-- 头指针表"尿布"指向此节点
           /   \
          /     \
   牛奶(4)       面包(1)  <-- 头指针表"面包"指向此节点（链表第一个节点）
    /  \   \          \
   /    \    \         \
面包(2) 啤酒(1) 可乐(1)  啤酒(1)  <-- 头指针表"啤酒"指向此节点（链表第一个节点）
  │                     /
  ▼                    ▼
啤酒(1)             可乐(1)  <-- 头指针表"可乐"指向此节点（链表第一个节点）
（头指针表"面包"链表第二个节点）

说明：👇

节点支持度：表示包含该节点路径的事务数（如“尿布(5)”表示5条事务包含尿布）。
头指针表链表（示例）：
- 面包的节点链表：(尿布→牛奶→面包(2)) → (尿布→面包(1))（两个节点，支持度合计3，对应面包的总支持度）。
- 啤酒的节点链表：(尿布→牛奶→啤酒(1)) → (尿布→牛奶→面包→啤酒(1)) → (尿布→面包→啤酒(1))（三个节点，支持度合计3）。

三、步骤3：挖掘频繁项集（以“啤酒”为例）

目标：通过头指针表自底向上（从“可乐”到“尿布”）挖掘，此处以“啤酒”为例，展示条件模式基和条件FP树的构建。
Step 1：获取“啤酒”的条件模式基

头指针表中“啤酒”的节点链表（共3个节点）：

  节点1：路径[尿布→牛奶→啤酒(1)] → 前缀路径：[尿布, 牛奶]，支持度=1  
  节点2：路径[尿布→牛奶→面包→啤酒(1)] → 前缀路径：[尿布, 牛奶, 面包]，支持度=1  
  节点3：路径[尿布→面包→啤酒(1)] → 前缀路径：[尿布, 面包]，支持度=1

条件模式基（前缀路径+支持度）：

  { [尿布,牛奶]:1, [尿布,牛奶,面包]:1, [尿布,面包]:1 }

Step 2：构建“啤酒”的条件FP树

统计前缀路径中各项的总支持度：
尿布：1+1+1=3，牛奶：1+1=2，面包：1+1=2（均≥2，保留）。
按支持度降序排序前缀项：[尿布(3), 牛奶(2), 面包(2)]。
插入前缀路径生成条件FP树：

        根节点
          |
        尿布(3)
        /     \
  牛奶(2)    面包(1) 
      |
  面包(1)

注意：{尿布,面包}的支持度是1，但由于面包（1+1）的支持度≥2，所以保留。
Step 3：从条件FP树挖掘频繁项集:

1-项集：{啤酒}（支持度=3）。
2-项集：{尿布,啤酒}(3)、{牛奶,啤酒}(2)、{面包,啤酒}(2)。
3-项集：{尿布,牛奶,啤酒}(2)、{尿布,面包,啤酒}(2)。

FP-Growth vs. Apriori 算法对比

特性	Apriori	FP-Growth
核心原理	产生-测试 (Generate-and-test)	分而治之 (Divide-and-conquer)
关键步骤	1. 连接步：生成候选集 2. 剪枝步：验证支持度	1. 构建FP树 2. 挖掘条件模式基
候选项集	需要生成，数量可能非常巨大（如L₂有10个候选集）	无需生成（直接从FP树挖掘），完全避免此开销
数据库扫描	多次扫描（每次计算支持度都需扫描）	通常仅需扫描两次（创建F-list和构建FP树）
运行效率	较慢，尤其在1项集很大时，性能下降严重	非常高效，通常比Apriori快一个数量级
内存开销	主要消耗在存储海量候选项集及其计数上	主要消耗在构建紧凑的FP-tree数据结构上
数据结构	使用简单的集合或列表	使用复杂的FP-tree和头指针表

4.垂直数据格式挖掘频繁项集-Eclat

Eclat

定义

前面介绍过的Apriori算法和FP-growth算法都是从TID项集格式（即｛TID：itemset｝）的事务集中挖掘频繁模式，其中TID是事务标识符，而itemset是事务TID中购买的商品。这种数据格式称为水平数据格式。或者，数据也可以用项-TID集格式（即｛item：TID_set｝）表示，其中item是项的名称，而TIDb_set是包含item的事务的标识符集合。这种格式称为垂直数据格式。 其中最著名的算法是 Eclat（Equivalence CLAss Transformation）。它与 Aclat（Apriori）和 FP-Growth 的“水平数据格式”有着根本性的不同。

3.3.1.核心思想：从水平到垂直的视角转换

水平数据格式（Horizontal Format）：也就是我们最常见的交易记录格式。每一行是一个交易（TID），记录了这个交易包含了哪些项（Items）。

原始事务数据库（TID：商品集）：

TID	商品（Items）
T1	`{牛奶, 面包, 尿布}`
T2	`{啤酒, 尿布, 面包, 可乐}`
T3	`{牛奶, 尿布, 啤酒}`
T4	`{面包, 牛奶, 尿布, 啤酒}`
T5	`{尿布, 牛奶, 可乐}`

垂直数据格式（Vertical Format）：将数据“翻转”。每一行是一个项（Item），记录了这个项出现在哪些交易中（TID列表，也称为 TID集）。

尿布: [T1, T2, T3, T4, T5]  （支持度=5）  
牛奶: [T1, T3, T4, T5]      （支持度=4）  
面包: [T1, T2, T4]          （支持度=3）  
啤酒: [T2, T3, T4]          （支持度=3）  
可乐: [T2, T5]              （支持度=2）

核心优势：在垂直格式下，任何项集的支持度计数可以通过对其TID集进行交集操作来轻松获得。
项集 {A, C} 的支持度 = |TID(A) ∩ TID(C)| = |{T1, T2} ∩ {T1, T2}| = |{T1, T2}| = 2

3.3.2.挖掘过程：Eclat 算法

Eclat 算法基于垂直数据格式，采用深度优先搜索（DFS）策略来挖掘频繁项集。

我们用一个例子来详解。假设数据库和最小支持度 min_sup = 2。
采用上面Apriori的演示案例，这样方便对比

Step 1：挖掘1-项集（L₁）,可以直接取预处理后的频繁1-项集：

L₁ = { {尿布}, {牛奶}, {面包}, {啤酒}, {可乐} }

Step 2：挖掘2-项集（L₂）
对每个1-项集，与其后的所有1-项集求TID List交集，支持度=交集长度≥2。
如：尿布∩牛奶,尿布∩面包,尿布∩啤酒,尿布∩可乐，依次类推。
如：牛奶∩可乐 => [T1, T3, T4, T5] ∩ [T2, T5] = [T5] ,支持度=1 不满足min_sup=2，不加入L₂
按照上面的计算方式，最终得到：👇
L₂ = { {尿布,牛奶}, {尿布,面包}, {尿布,啤酒}, {尿布,可乐}, {牛奶,面包}, {牛奶,啤酒}, {面包,啤酒} }

Step 3：挖掘3-项集（L₃）
对每个2-项集，与其后的2-项集（共享前缀）求交集（仅保留包含相同前缀的项集，如{尿布,牛奶}的后续项集为含“尿布,牛奶”前缀的项集，或按顺序与后续单项求交）。

Step 4：挖掘4-项集（L₄）
对3-项集与其后的项集求交集，支持度均<2，终止。

最终频繁项集（与Apriori、FP-Growth结果一致）

Eclat算法的优势（对比Apriori和FP-Growth） 👇

垂直数据格式高效存储：
- Apriori和FP-Growth基于水平数据格式（每条事务为一行），Eclat采用垂直格式（每个项的TID List），支持度计算通过TID List交集实现，无需扫描原始事务，尤其适合高维数据。
无候选集生成，直接求交集：
- Apriori需生成大量候选集并验证支持度；Eclat通过递归交集运算直接生成高阶项集的TID List，避免候选集冗余（如{尿布,牛奶,面包}直接由{尿布,牛奶}与面包的TID List交集生成）。
深度优先搜索，内存效率高：
- FP-Growth依赖FP树的构建和遍历，对内存占用较高；Eclat通过TID List交集递归挖掘，可按项集顺序分批处理，内存消耗更可控，尤其适合磁盘存储的大规模数据。
支持度计算时间复杂度低：
- 交集运算可通过 bitmap或哈希表高效实现（如两个有序TID List的交集时间复杂度为O(m+n)，m、n为列表长度），比Apriori的数据库扫描更高效。

5.关联模式评估

实操

定义

大部分关联规则挖掘算法都使用支持度-置信度框架。尽管最小支持度和置信度阈值可以排除大量无趣规则的探查，但仍然会有一些用户不感兴趣的规则存在。当使用低支持度阈值挖掘或挖掘长模式时，这种情况尤为严重。

5.1 强关联规则不一定是有趣的：

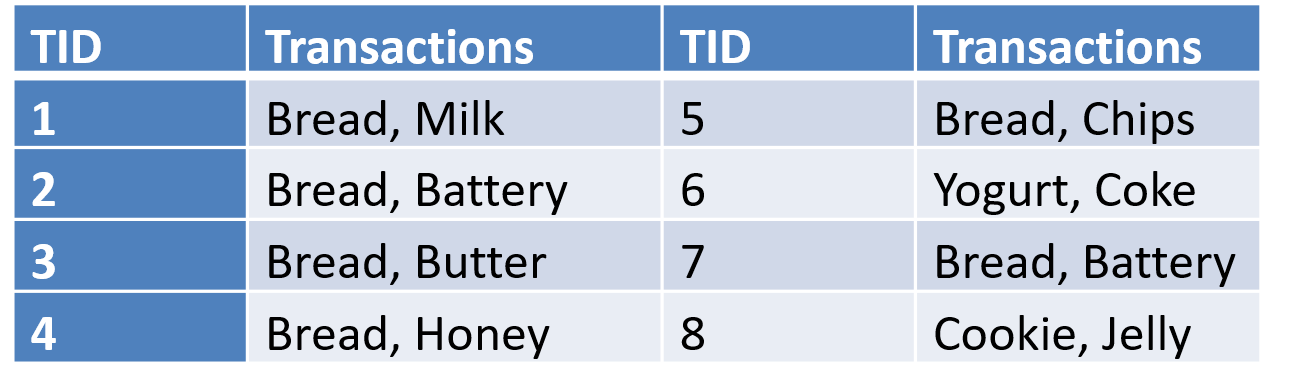
从上图的数据集中可以看到，置信度P(Bread|Battery=100% > P(Bread))=75% 但是 Battery=> Bread 并不是有趣的模式。应该是典型的伪关联。

那么如何避免“伪关联”？ 👇

5.2 从关联分析到相关分析

为挖掘“有趣的模式”，需在支持度、置信度基础上，进一步筛选：

提升度（Lift）> 1：确保 A 对 B 有实际提升效果（排除因 B 本身普遍导致的高置信度）。
卡方检验：验证规则的统计显著性，排除小样本随机误差。
领域知识：结合实际场景判断（如“电池和面包”在购物逻辑上无明显关联，而“面包和牛奶”更可能是真正相关的模式）。

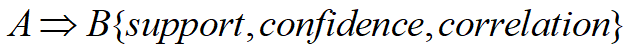
由此看出，相关规则不仅用支持度和置信度度量，还增加了项集A和B之间的相关性度量（Correlation）。可以选择使用的相关性度量较多，常用的有提升度(Lift) 和卡方检验（χ²）。

卡方检验：是非参数检验中的一个统计量,主要用于检验数据的相关性。
卡方检验的公式为：

其中卡方值越大，相关性越强。

6.实操- Apriori算法应用

实操

定义

安装apyori包和检查xlrd版本

%pip install apyori

import xlrd
print(xlrd.__version__)  # 输出应为 >=2.0.1，例如：2.0.2```

加载数据(将data.xlsx文件中的数据加载.ipynb的同级目录)👇

import pandas as pd #数据处理库，用于读取Excel文件、数据清洗和转换。
from apyori import apriori #导入Apriori算法（来自apyori库），用于挖掘频繁项集和关联规则。
df = pd.read_excel("data.xls") # 加载数据
df.head() # 查看前5行数据，了解数据结构（如列名、数据格式）
df.info() # 查看数据信息：列数、行数、数据类型、缺失值情况
df.describe() # 查看数值型列的统计描述（如计数、均值、最值，此处可能主要用于`OrderID`等）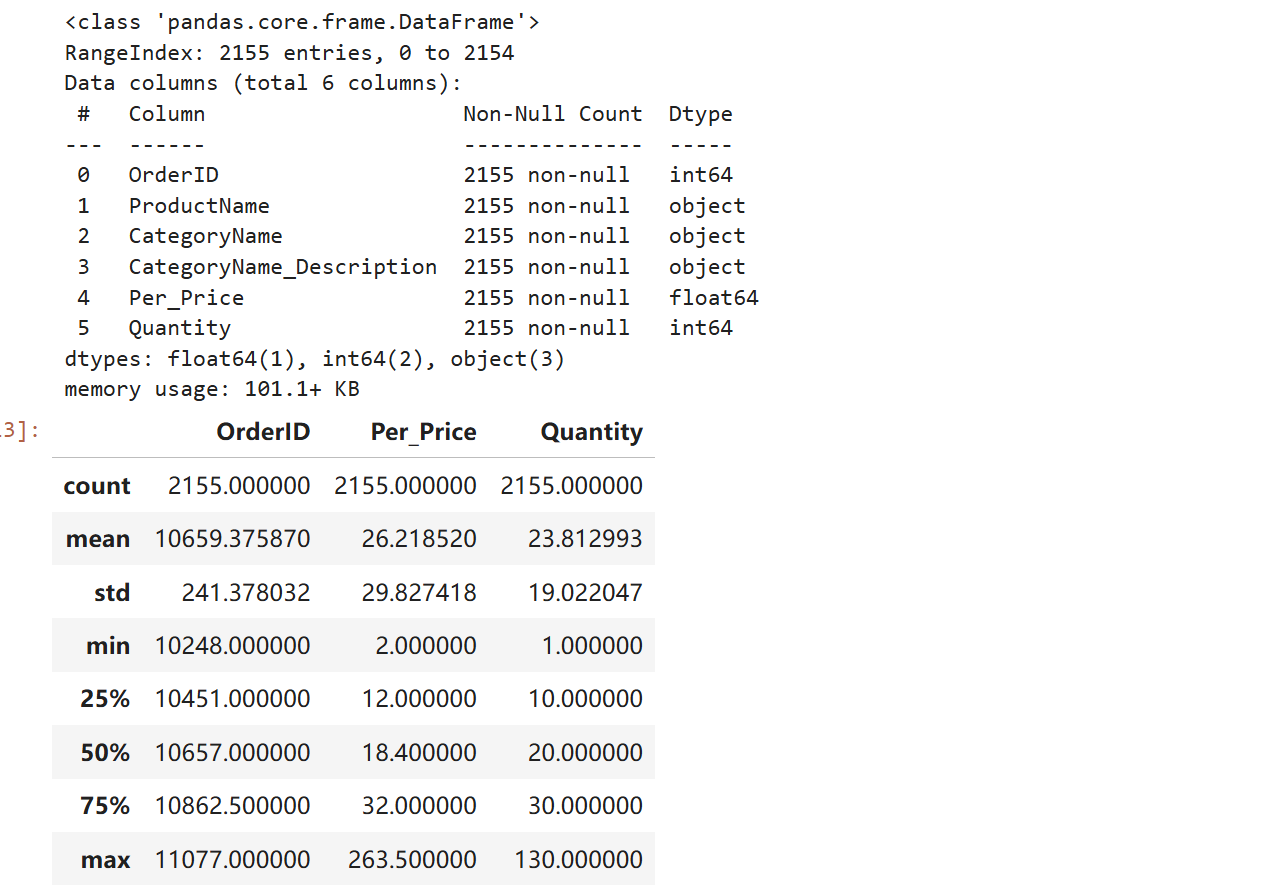

获取项集

#将原始数据转换为Apriori算法要求的交易列表格式（transactions）。
#groupby(by='OrderID')：按订单ID分组，确保每个订单对应一条交易记录。
#apply(lambda x: list(x.CategoryName))：对每个订单组，将其中的CategoryName（商品类别）转换为列表，代表该订单购买的所有商品（即“项集”）。
#示例：若某订单包含商品[乳制品, 面包, 尿布]，则transactions中会新增一条记录['乳制品', '面包', '尿布']。
transactions = df.groupby(by='OrderID').apply(lambda x: list(x.CategoryName)) 、
transactions.head(6) # 查看前6条交易记录，了解数据格式

进行关联规则挖掘

min_supp = 0.1  # 最小支持度
min_conf = 0.1  # 最小置信度
min_lift = 0.1  # 最小提升度
result = list(apriori(transactions=transactions, 
           min_support=min_supp,    # 步骤1：筛选频繁项集
           min_confidence=min_conf, # 步骤2：从频繁项集中生成规则，并按置信度筛选
           min_lift=min_lift))      # 步骤2：继续按提升度筛选规则
print(result) # 打印挖掘结果
# apriori：关联规则挖掘算法
# transactions=transactions  数据集
# min_support=min_supp  最小支持度
# min_confidence=min_conf  最小置信度
# min_lift=min_lift  最小提升度
# result  挖掘结果

显示关联的挖掘规则

supports=[]# 支持度
confidences=[]# 置信度
lifts=[]# 提升度
bases=[]# 基础项集
adds=[]# 添加项集
for r in result:
    for x in r.ordered_statistics:
        supports.append(r.support)
        confidences.append(x.confidence)
        lifts.append(x.lift)
        bases.append(list(x.items_base))
        adds.append(list(x.items_add))

# 显示关联规则      
resultshow = pd.DataFrame({
    'support':supports,
    'confidence':confidences,
    'lift':lifts,
    'base':bases,
    'add':adds})

resultshow.tail(8) # 显示最后8条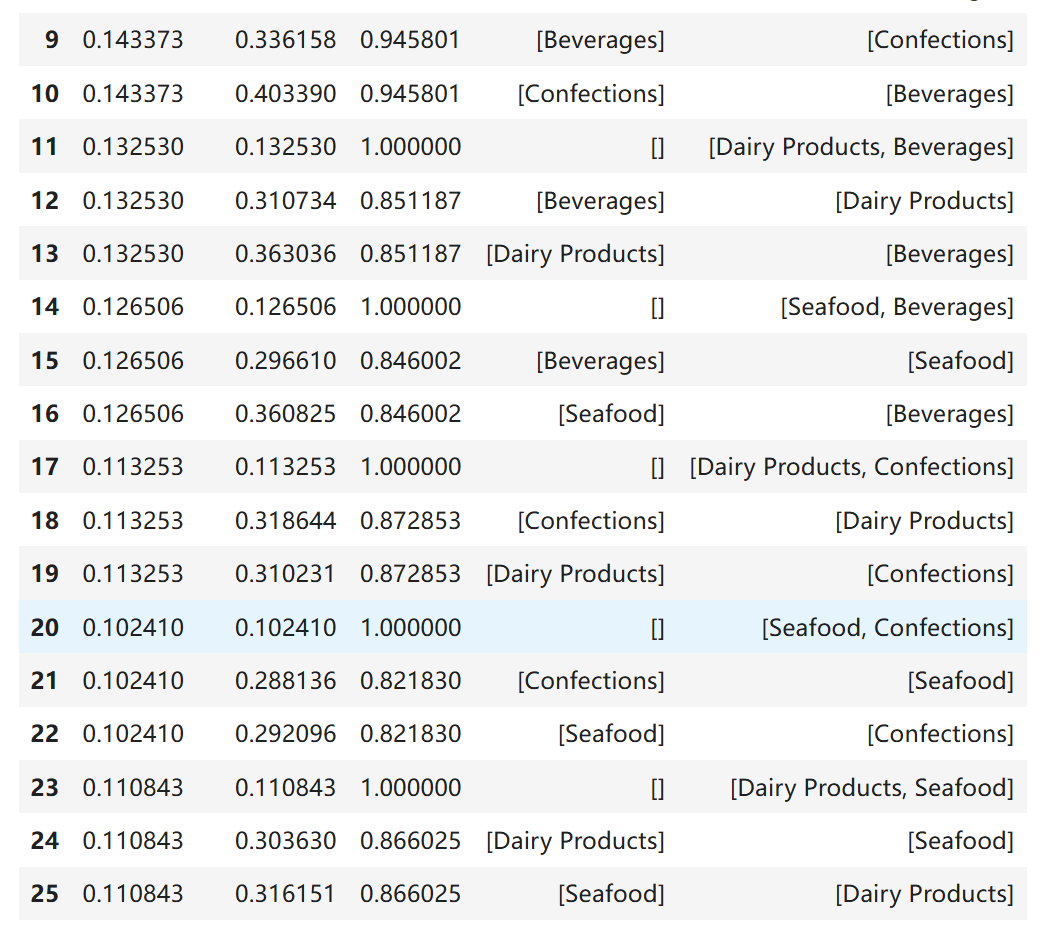

- 支持度（support）：规则在所有交易中出现的频率（本例中均≈0.1，接近最小支持度阈值，普遍性较低）。
- 置信度（confidence）：规则A→B的可靠性（如confidence=0.3表示30%的A订单会购买B）。
- 提升度（lift）：规则的“意外性”（lift>1表示A对B有正向提升，lift=1表示独立，lift<1表示负相关）。

- 行18：
    - support:同时购买“糖果（Confections）”和“乳制品（Dairy Products）”的订单占比11.3%。
    - confidence:购买糖果的顾客中，31.9%会同时购买乳制品。
    - liftL:lift<1：购买糖果后，购买乳制品的概率反而比“不买糖果时”低12.7%（负相关）。
> 结论：无价值规则，糖果与乳制品可能存在替代关系（或顾客购买糖果后倾向于不买乳制品）。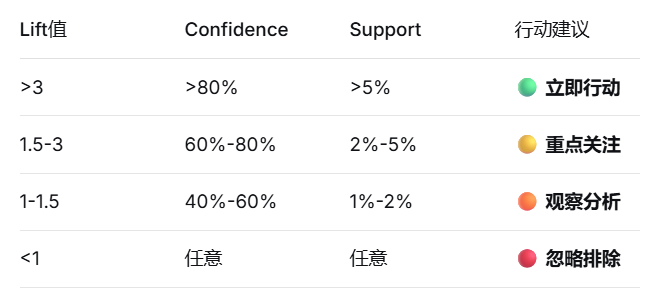

使用Fp-growth算法

教材没有涉及，但是在实际应用中，Fp-growth算法的性能要优于Apriori算法。

在运行前，需要安装 mlxtend 库：

%pip install mlxtend

import pandas as pd
from mlxtend.frequent_patterns import fpgrowth, association_rules
from mlxtend.preprocessing import TransactionEncoder

# 读取数据
df = pd.read_excel("data.xls")

# 创建事务列表
transactions = df.groupby('OrderID')['CategoryName'].apply(list).tolist()

# 使用TransactionEncoder进行编码（更高效的方法）
te = TransactionEncoder()
te_ary = te.fit(transactions).transform(transactions)
encoded_df = pd.DataFrame(te_ary, columns=te.columns_)

# 设置阈值
min_supp = 0.1
min_conf = 0.1
min_lift = 0.1

# FP-Growth 算法
frequent_itemsets = fpgrowth(encoded_df, min_support=min_supp, use_colnames=True)

# 生成关联规则
if len(frequent_itemsets) > 0:
    rules = association_rules(frequent_itemsets, metric="confidence", min_threshold=min_conf)
    rules = rules[rules['lift'] >= min_lift]
    
    # 格式化结果
    resultshow = pd.DataFrame({
        'support': rules['support'],
        'confidence': rules['confidence'],
        'lift': rules['lift'],
        'base': rules['antecedents'].apply(list),
        'add': rules['consequents'].apply(list)
    }).sort_values('support', ascending=False)
    
    print("FP-Growth 算法结果:")
    print(f"总规则数: {len(resultshow)}")
    print("\n最后8条规则:")
    print(resultshow.tail(8))

使用Eclat算法

教材中没有涉及，但是在实际应用中，Eclat算法的性能要优于Apriori算法。

也需要安装 mlxtend 库，

import pandas as pd
from mlxtend.frequent_patterns import fpgrowth  # 使用fpgrowth作为Eclat的替代
from mlxtend.preprocessing import TransactionEncoder

# 读取数据
df = pd.read_excel("data.xls")

# 创建事务列表
transactions = df.groupby('OrderID')['CategoryName'].apply(list).tolist()

# 使用TransactionEncoder进行编码
te = TransactionEncoder()
te_ary = te.fit(transactions).transform(transactions)
encoded_df = pd.DataFrame(te_ary, columns=te.columns_)

# 设置最小支持度阈值
min_supp = 0.1

print("使用 Eclat 算法挖掘频繁项集...")

# Eclat 算法 - 使用 fpgrowth 只挖掘频繁项集（Eclat的核心功能）
frequent_itemsets = fpgrowth(encoded_df, 
                            min_support=min_supp, 
                            use_colnames=True,
                            max_len=None)  # 不限制项集长度

print(f"找到 {len(frequent_itemsets)} 个频繁项集")

# 按支持度降序排列
frequent_itemsets = frequent_itemsets.sort_values('support', ascending=False)

# 显示结果
print("\n前10个频繁项集（支持度最高）:")
for idx, row in frequent_itemsets.head(10).iterrows():
    itemset = list(row['itemsets'])
    support = row['support']
    print(f"项集: {itemset}, 支持度: {support:.3f}")

print("\n最后8个频繁项集:")
for idx, row in frequent_itemsets.tail(8).iterrows():
    itemset = list(row['itemsets'])
    support = row['support']
    print(f"项集: {itemset}, 支持度: {support:.3f}")

# 保存结果到DataFrame
resultshow = pd.DataFrame({
    'support': frequent_itemsets['support'],
    'itemset': frequent_itemsets['itemsets'].apply(list)
})

print(f"\n总频繁项集数量: {len(resultshow)}")