数据仓库与数据挖掘-第一章节

通过本课的学习，学生应该掌握如下知识：

1.数据归约

数据归约

定义

1.为什么需要数据规约？

问题：数据太大 → 计算慢、存储贵、分析难
解决：像整理房间一样整理数据，只保留"有用的"部分
三大招数：

• 维归约（砍掉没用的列）
• 数量规约（砍掉没用的行）
• 数据压缩（把数据"压扁"存储）

2.维归约：删除多余的"列"

核心思想：数据表中的很多列（特征）是重复或无关的，直接删掉！

2.1 数据降维与压缩典型方法对比表

方法	通俗解释	例子	适用场景
主成分分析（PCA） ❤️	把多个列合并成少数"超级列"	用"身材指数"代替"身高+体重"	特征高度相关的数值数据（如传感器数据）
属性子集选择 🚀	直接扔掉不重要的列	预测房价时忽略"门牌号"列	特征冗余明显的结构化数据（如表格数据）
小波变换🚀	把图像拆解成"轮廓+细节"，压缩细节部分	照片存为模糊版+边缘修正包	图像/信号压缩（如JPEG2000、心电图压缩）

应用场景：小波变换压缩图像

后期讲解傅里叶变换时，在详细讲解小波变换

2.2 主成分分析（PCA）

image

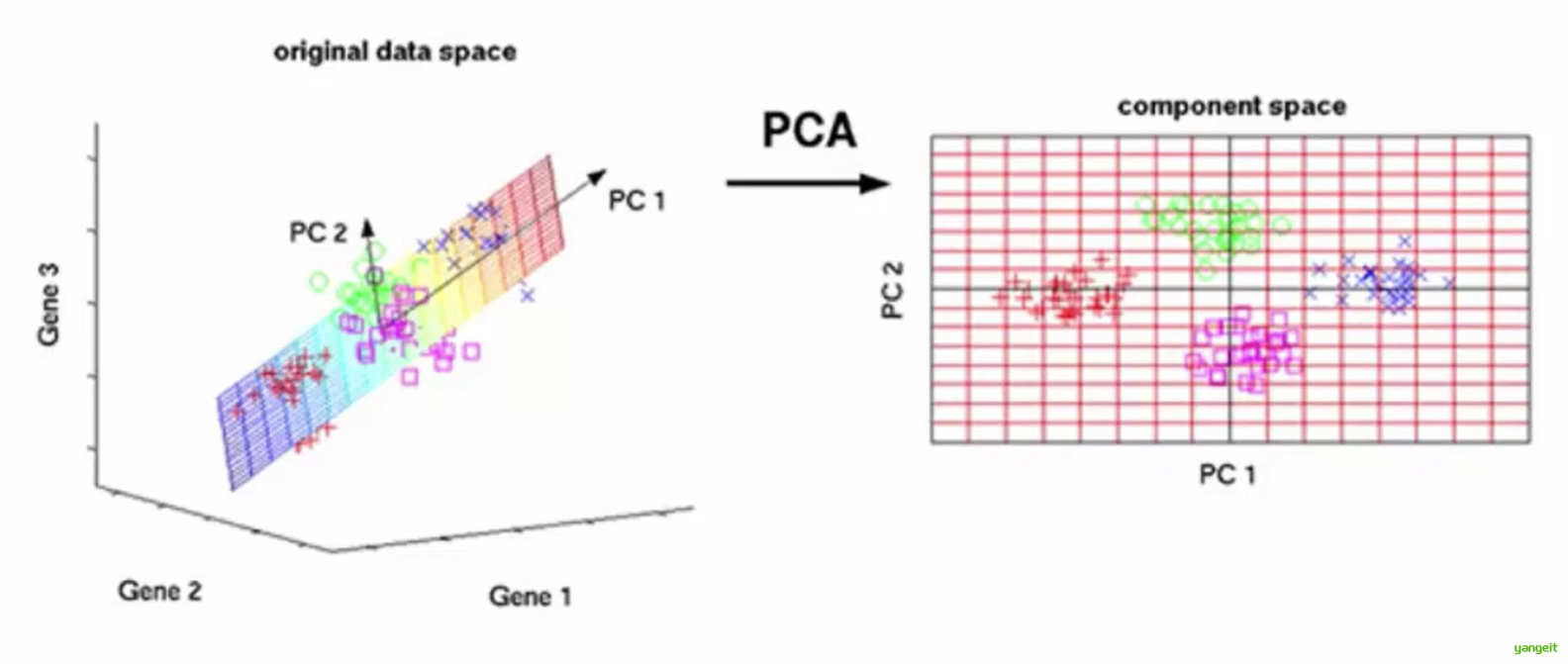
通俗理解：结合上图，3维空间中存在一组数据，但是无法知道这组数据中哪些是重要的，可以通过pca降维的方式，降低到2维空间，然后通过2维空间的坐标，来判断这组数据中哪些是重要的。

【例3-36】sklearn实现鸢尾花数据降维，将原来4维的数据降维为2维。

image

iris数据集的中文名是安德森鸢尾花卉数据集，英文全称是Anderson’s Iris data set。iris包含150个样本，对应数据集的每行数据。每行数据包含每个样本的四个特征和样本的类别信息，所以iris数据集是一个150行5列的二维表 。

通俗地说，iris数据集是用来给花做分类的数据集，内包含 3 种类别，分别为山鸢尾（Iris-setosa）、变色鸢尾（Iris-versicolor）和维吉尼亚鸢尾（Iris-virginica）,每个样本包含了花萼长度、花萼宽度、花瓣长度、花瓣宽度四个特征（前4列），我们需要建立一个分类器，分类器可以通过样本的四个特征来判断样本属于山鸢尾、变色鸢尾还是维吉尼亚鸢尾（这三个名词都是花的品种）。

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

# 加载鸢尾花数据集
data = load_iris()
X = data.data  # 原始特征 (150个样本 x 4个特征)
y = data.target  # 类别标签 (0, 1, 2)
target_names = data.target_names  # 类别名称

# PCA降维 (4维 -> 2维)
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)  # 降维后的数据 (150 x 2)

# 打印前5个样本的降维结果
print("降维后数据前5行：\n", X_reduced[:5])
print("各主成分解释方差比例：", pca.explained_variance_ratio_)

# 可视化

plt.figure(figsize=(8, 6))
colors = ['r', 'b', 'g']
markers = ['x', 'D', '.']

for i, target in enumerate(target_names):
    plt.scatter(X_reduced[y == i, 0],  # 第一主成分
               X_reduced[y == i, 1],  # 第二主成分
               c=colors[i],
               marker=markers[i],
               label=target)


# 添加图例和标签
plt.legend(loc='best')
plt.xlabel('pca1 (%.2f%%)' % (pca.explained_variance_ratio_[0]*100))
plt.ylabel('pca2 (: %.2f%%)' % (pca.explained_variance_ratio_[1]*100))
plt.title('kehsihua')
plt.grid(True)
plt.show()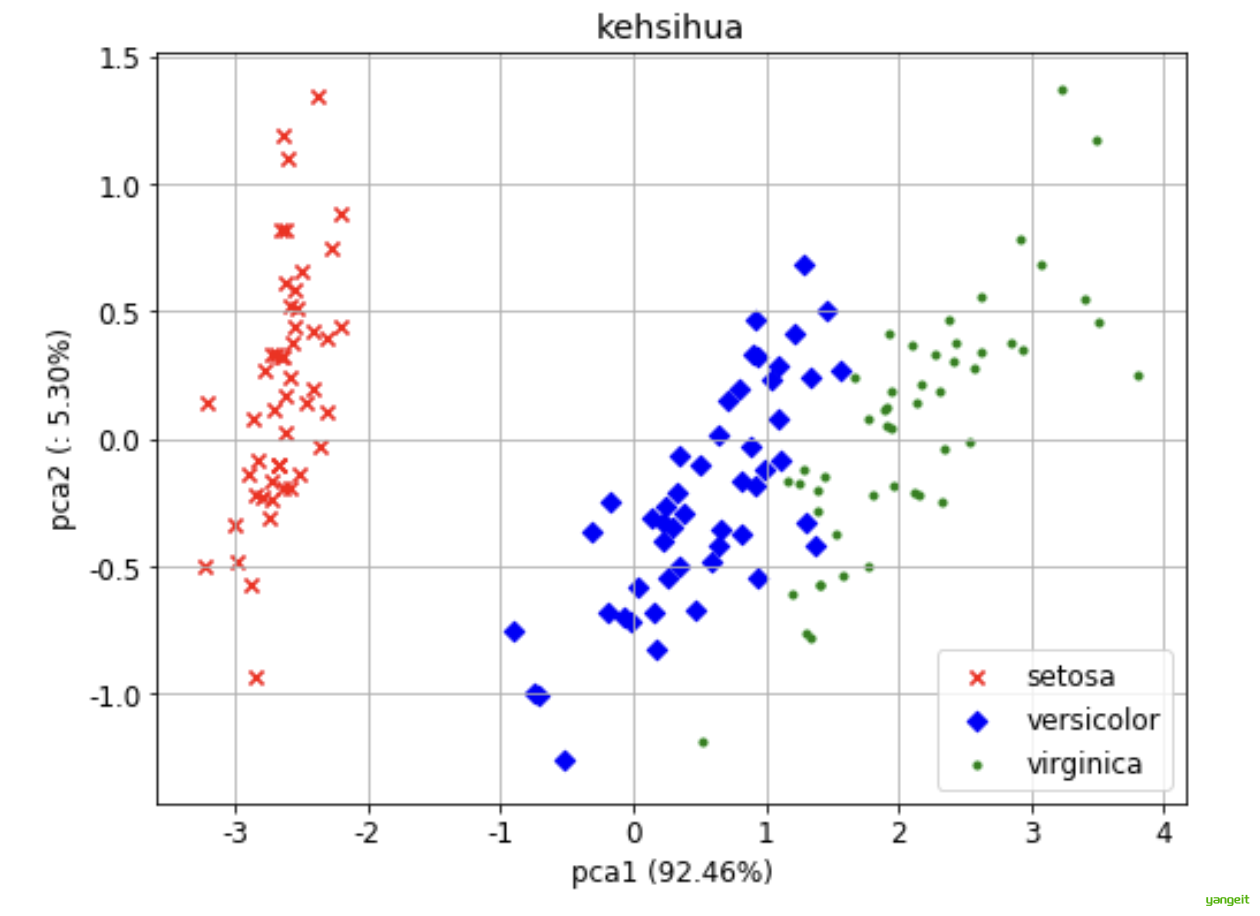

image

x轴（PC1）：将三类鸢尾花（Setosa, Versicolor, Virginica）按尺寸大小分开（Setosa明显较小）。
y轴（PC2）：进一步区分Versicolor和Virginica（可能反映花瓣形状差异）。

3. 数量规约：减少多余的"行"

典型方法

方法	通俗解释	例子
抽样	只分析部分数据（像尝汤判断咸淡）	从1亿条订单中随机抽1万条分析
聚类代表点	用中心点代表一群相似数据	用3个典型用户代表所有用户行为
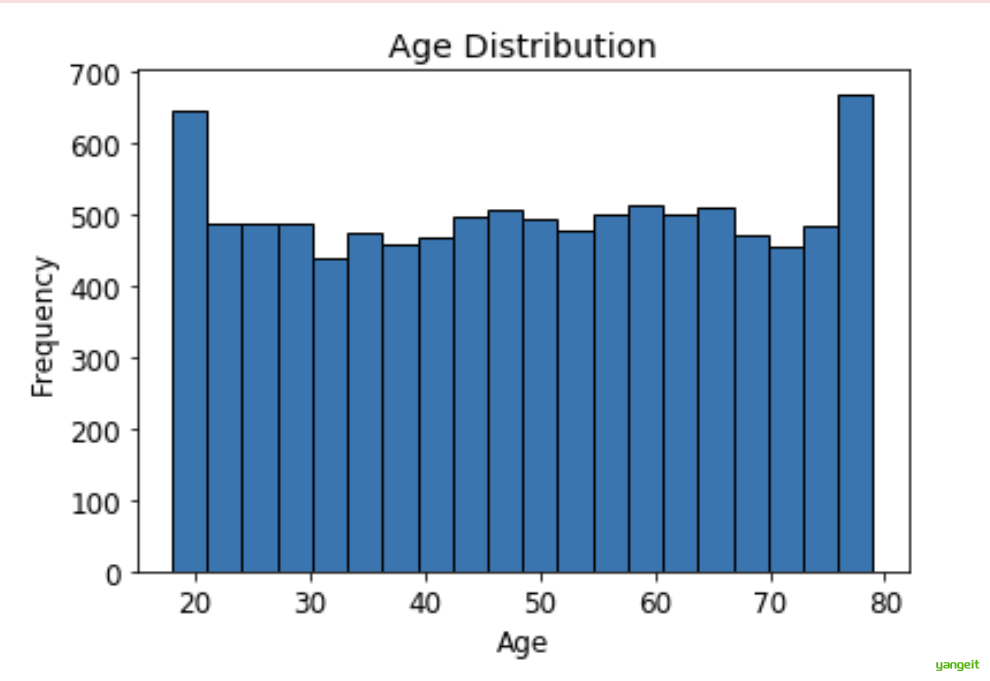
直方图	用分段统计代替原始数据	用"0-10岁、11-20岁…"代替具体年龄

直方图展示10000个样本的年龄分布

4. 数据压缩：用"缩写"存数据

典型方法

方法	通俗解释	例子
无损压缩	数据可完全还原（像数学公式化简）	存储"AAAAABBBB"为"5A4B"
有损压缩	牺牲少量精度换空间（像手机照片压缩）	小数点后保留2位代替6位，
编码优化	用更短的符号表示数据	用"1/0"代替"男/女" , i18n

如小波变换就是一种有损压缩，它把图像分成低频部分和高频部分，高频部分用较少的位表示，低频部分用较多的位表示，从而压缩数据。

总结

课堂作业

结合上一节内容，完成下列问题：

1. 为什么需要数据归约？
2. 数据归约的典型方法有哪些？通俗描述一下。

2.数据变换与数据离散化概要

数据变换与数据离散化

定义

1.为什么需要数据变换？

提升数据质量：去噪声、补缺失、统一格式。
提高挖掘效率：减少计算量（如聚集、离散化）。
增强模型效果：规范化避免偏差，概念分层支持多粒度分析。

2.数据变换策略形式👇

在数据变换中，数据被变换或统一成适合于挖掘的形式。数据变换策略包括如下几种:

1. 光滑（Smoothing）

• 作用：去除数据中的噪声（随机波动或异常值）
• 常用方法：
  • 分箱（Binning）将数据按区间分组（如“0-10, 11-20”），用组内均值/中位数替代原始值。
  • 回归（Regression）用拟合函数（如线性回归）平滑数据趋势。
  • 聚类（Clustering）通过聚类剔除离群点。
• 示例：传感器采集的温度数据可能存在瞬时波动，通过分箱或回归消除噪声。

2. 属性构造（Attribute Construction）

• 作用：通过已有属性构造新属性，提升数据表达能力。
• 示例：
  • 已有"长"和"宽" → 构造"面积=长×宽"
  • 电商数据中，“购买次数”和“平均金额”可构造“用户价值评分”。

3. 聚集（Aggregation）

• 作用：对数据进行汇总，减少数据量并突出宏观特征。
• 常用方法：
  • 时间维度（日→月→年）
  • 空间维度（城市→省份→国家）
• 示例：将每日销售额汇总为月度销售额

4. 规范化（Normalization）✏️ 🍐 ❤️

• 作用：将不同尺度的属性缩放到统一范围（如[0,1]），避免数值大的属性主导分析结果。
• 常用方法：
  • 最小-最大规范化（[0,1]区间）
  • Z-score标准化（基于均值和标准差）
• 示例：将“年龄（0-100岁）”和“收入（0-1,000,000元）”统一到[0,1]。

5. 离散化（Discretization）

• 作用：将连续数值转换为区间或分类标签，简化模型计算。
• 常用方法：
  • 等宽分箱
  • 等频分箱
• 示例：
  • “年龄”连续值 → 分段标签“儿童(0-12)”“青少年(13-20)”等。
  • 适用于决策树等分类算法

6. 概念分层（Concept Hierarchy）

• 作用：将低层类别属性泛化为高层概念，减少数据复杂度。
• 示例：
  • “街道名” → 泛化为“城市” → “国家”。
  • "商品ID" → "品类" → "大类"

总结

课堂作业

结合上述讲解，理解数据变换的策略形式，并回答下列问题：

1. 规范化和离散化有什么区别？
2. 规范化和上一节学过的归一化有什么区别？

2.1 数据变换之规范化

数据变换之规范化

定义

1.数据规范化

1. 最小-最大规范化

数学公式：v'=(v-min)/(max-min) 其中v'为规范化后的值，v为原始值，min为最小值，max为最大值。

2. Z-score标准化

数学公式：v'=(v-μ)/σ 其中v'为规范化后的值，v为原始值，μ为均值，σ为标准差。

案例1：数据规范化示例 🍐

import numpy as np
from sklearn.preprocessing import MinMaxScaler, StandardScaler

# 原始数据
data = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 使用dataframe格式显示
data1 = pd.DataFrame(data)

print("原始数据：\n", data1)
print("-------------场景1------------")
# 使用sklearn中的scale函数求x-trans 和均值 以及标准差
X_trans=preprocessing.scale(data) # x-trans是z-score标准化后的值
print("X_trans:",X_trans)
print("X_trans.mean:",X_trans.mean(axis=0)) #axis=0表示按列求均值，axis=1表示按行求均值
print("X_trans.std:",X_trans.std(axis=0))



# 使用sklearn中的MinMaxScaler和StandardScaler求解
print("-----------场景2--------------")
# 最小-最大规范化
scaler_minmax = MinMaxScaler()
data_minmax = scaler_minmax.fit_transform(data)
print("最小-最大规范化结果：\n", data_minmax)

# Z-score标准化
scaler_zscore = StandardScaler()
data_zscore = scaler_zscore.fit_transform(data)
print("Z-score标准化结果：\n", data_zscore)

运行结果：

原始数据：
    0  1  2
0  1  2  3
1  4  5  6
2  7  8  9
-------------场景1------------
X_trans:
 [[-1.22474487 -1.22474487 -1.22474487]
 [ 0.          0.          0.        ]
 [ 1.22474487  1.22474487  1.22474487]]
X_trans.mean:
 [0. 0. 0.]
X_trans.std:
 [1. 1. 1.]
-----------场景2--------------
最小-最大规范化结果：
 [[0.  0.  0. ]
 [0.5 0.5 0.5]
 [1.  1.  1. ]]
Z-score标准化结果：
 [[-1.22474487 -1.22474487 -1.22474487]
 [ 0.          0.          0.        ]
 [ 1.22474487  1.22474487  1.22474487]]

从结果可知，最小-最大规范化将原始数据按列缩放到[0,1]区间，Z-score标准化将原始数据按列缩放到均值为0，标准差为1的正态分布。
说明数据规范化可以将不同尺度的数据缩放到统一范围，避免数值大的属性主导 分析结果。

2.2 数据变换之哑变量

数据变换之哑变量

定义

类别型数据的哑变量处理 ✏️ 🍐

为什么要这样处理？ 👇

• 作用：将分类变量转换为数值变量，便于模型处理。
• 示例：将性别（男、女）转换为二值变量（0、1）。

案例1：类别型数据的哑变量处理 🍐

类别型数据（Categorical Data）是指取值限于有限集合的数据，例如：

• 性别：男、女
• 颜色：红、绿、蓝
• 城市：北京、上海、广州
  这些数据通常是非数值型的，但机器学习模型（如线性回归、神经网络）只能处理数值型输入，因此需要转换为数值形式。

聪明的你立马想到了用数字编码来实现😃，例如：

• 性别：男=1、女=2
• 颜色：红=1、绿=2、蓝=3
• 城市：北京=1、上海=2、广州=3

但是，这样做有一个问题：😳

• 无法区分“男”和“女”的区别，无法区分“红”和“绿”的区别。
• 无法处理新出现的类别，例如：颜色出现了“紫”。
• 无法处理缺失值，例如：颜色缺失了“黄”。
• 无法处理有序类别，例如：颜色有“红>橙>黄>绿>蓝>靛>紫”的顺序关系。

因此，我们需要一种方法，将类别型数据转换为数值型数据，同时保留类别之间的区别和关系。这就是哑变量处理（Dummy Variable）。

哑变量处理将每个类别转换为一个二进制向量：

原始数据：颜色 = ["红", "绿", "蓝"]
哑变量编码后：
红 → [1, 0, 0]
绿 → [0, 1, 0]
蓝 → [0, 0, 1]

优点： 👇

• 消除虚假顺序 所有类别在数值上平等（如 红 和 绿 的距离与 红 和 蓝 相同）。
• 兼容模型 满足机器学习模型对数值输入的要求（如线性回归、SVM、神经网络）。
• 避免权重偏差 防止模型将类别数字误判为连续变量（如 城市=3 比 城市=1 更重要）。

缺点： 👇

• 维度爆炸：如果类别很多（如邮政编码），编码后特征维度会急剧增加。

import pandas as pd

data = pd.DataFrame({"颜色": ["红", "绿", "蓝"]}) # 创建一个包含颜色数据的DataFrame
print(data) # 打印原始数据 
encoded_data = pd.get_dummies(data) # 使用get_dummies函数进行哑变量编码
print(encoded_data) # 打印编码后的数据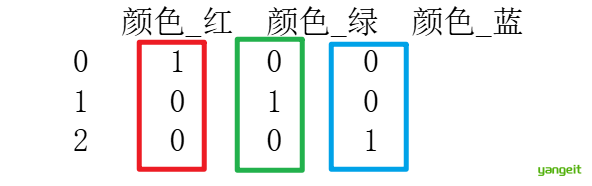

image

在机器学习中，哑变量处理通常用于分类问题，常常使用one-hot编码（One-Hot Encoding）。
One-Hot编码是一种将分类变量转换为二进制向量的方法，其中每个类别对应一个二进制位，且每个样本的向量中只有一个位置为1，其余位置为0。
可以使用sklearn中的OneHotEncoder类来实现One-Hot编码。

from sklearn.preprocessing import OneHotEncoder

enc = OneHotEncoder()# 创建OneHotEncoder对象
# 案例1
X = [["红"], ["绿"], ["蓝"], ["黄"]]  # 创建一个包含颜色数据的列表
enc.fit(X) # 拟合数据
R1=enc.transform(X).toarray() # 转换数据
print('案例1：\n',R1) # 打印转换后的数据

# 案例2 
X1=[["女","18-25岁","本科","10000"],["男","26-35岁","硕士","20000"],["男","36-45岁","博士","30000"],["女","46-55岁","博士后","40000"]]
enc.fit(X1) # 拟合数据
# 打印特征
print('特征名称:\n',enc.get_feature_names_out())
R2=enc.transform(X1).toarray() # 转换数据
print('案例2：\n',R2) # 打印转换后的数据

运行结果

案例1：
 [[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 1.]]
特征名称:
 ['x0_女' 'x0_男' 'x1_18-25岁' 'x1_26-35岁' 'x1_36-45岁' 'x1_46-55岁' 'x2_博士'
 'x2_博士后' 'x2_本科' 'x2_硕士' 'x3_10000' 'x3_20000' 'x3_30000' 'x3_40000']
案例2：
 [[1. 0. 1. 0. 0. 0. 0. 0. 1. 0. 1. 0. 0. 0.]
 [0. 1. 0. 1. 0. 0. 0. 0. 0. 1. 0. 1. 0. 0.]
 [0. 1. 0. 0. 1. 0. 1. 0. 0. 0. 0. 0. 1. 0.]
 [1. 0. 0. 0. 0. 1. 0. 1. 0. 0. 0. 0. 0. 1.]]

案例1：是典型的 单列分类变量 的 One-Hot 编码结果。
每一行代表一个样本，每一列代表一个类别。
只有一个 1，其余为 0，表示样本属于某个特定类别

案例2：是典型的 多列分类变量的联合编码。
以第一行 ["女","18-25岁","本科","10000"] 为例：

• x0_女=1（性别女），x0_男=0
• x1_18-25岁=1（年龄组），其他年龄=0
• x2_本科=1（学历），其他学历=0
• x3_10000=1（收入），其他收入=0

总结

课堂作业

学习完上一节，完成下列问题：

1. 参考上述代码，在jyupyter notebook中实现最小-最大规范化、Z-score标准化、类别型数据的哑变量处理、数据离散化等数据预处理方法。
2. 简述哑变量处理的作用

2.3.数据变换之离散化

数据变换之离散化

定义

数据离散化

数据分析和统计的预处理阶段，经常会遇到年龄，消费，等连续型数据，这些数据在分析时，往往需要离散化处理，将连续型数据转换为离散型数据，以便于：

• 简化模型（如决策树、朴素贝叶斯更适合离散特征）。
• 减少噪声影响（如极端值的影响）。
• 增强可解释性（如“高收入”比“年收入 98372 元”更直观）。

常用的离散方法有：👇

• 等宽分箱
• 等频分箱
• 聚类分箱

案例3：等宽分箱 🍐

原理：将数据范围均匀分成若干个宽度相同的区间。
公式：区间宽度 = (最大值 - 最小值) / 箱数

案例：年龄分组（分 3 组）

import pandas as pd

# 原始数据
data = pd.DataFrame({"年龄": [25, 30, 35, 40, 45, 50, 55, 60, 65, 70]})

# 等宽分箱
bins = [0, 30, 50, 100]  # 定义区间边界
data["年龄分组"] = pd.cut(data["年龄"], bins=bins, labels=["青年", "中年", "老年"])

print(data)

image

✅ 简单直观，易于实现。
❌ 对异常值敏感（如最大值远高于其他值会导致分组不均）

案例4：等频分箱 🍐

原理：将数据按频率 分成若干个区间，每个区间的样本数量相同。
公式：区间数量 = 数据总数 / 每个区间的样本数量

案例：年龄分组（每个区间 3 个样本）

import pandas as pd

# 原始数据
data = pd.DataFrame({"年龄": [25, 30, 35, 40, 45, 50, 55, 60, 65, 70]})
# 等频分箱
bins = [0, 30, 50, 100]  # 定义区间边界
data["年龄分组"] = pd.qcut(data["年龄"], q=3, labels=["青年", "中年", "老年"])  
#q=3 表示使用3分位数（即第33.3%和第66.6%分位数作为切分点），最终分成3组，每组占比约33.3%

print(data)

运行结果：

   年龄 年龄分组
0  25   青年
1  30   青年
2  35   青年
3  40   青年
4  45   中年
5  50   中年
6  55   中年
7  60   老年
8  65   老年
9  70   老年

✅ 避免数据分布不均问题。
❌ 可能将相近值分到不同组（如 25 和 30 被分开）。

案例5 ：聚类分箱 🍐❤️

原理用聚类算法（如 K-Means）将数据按相似性分组（默认使用欧氏距离)。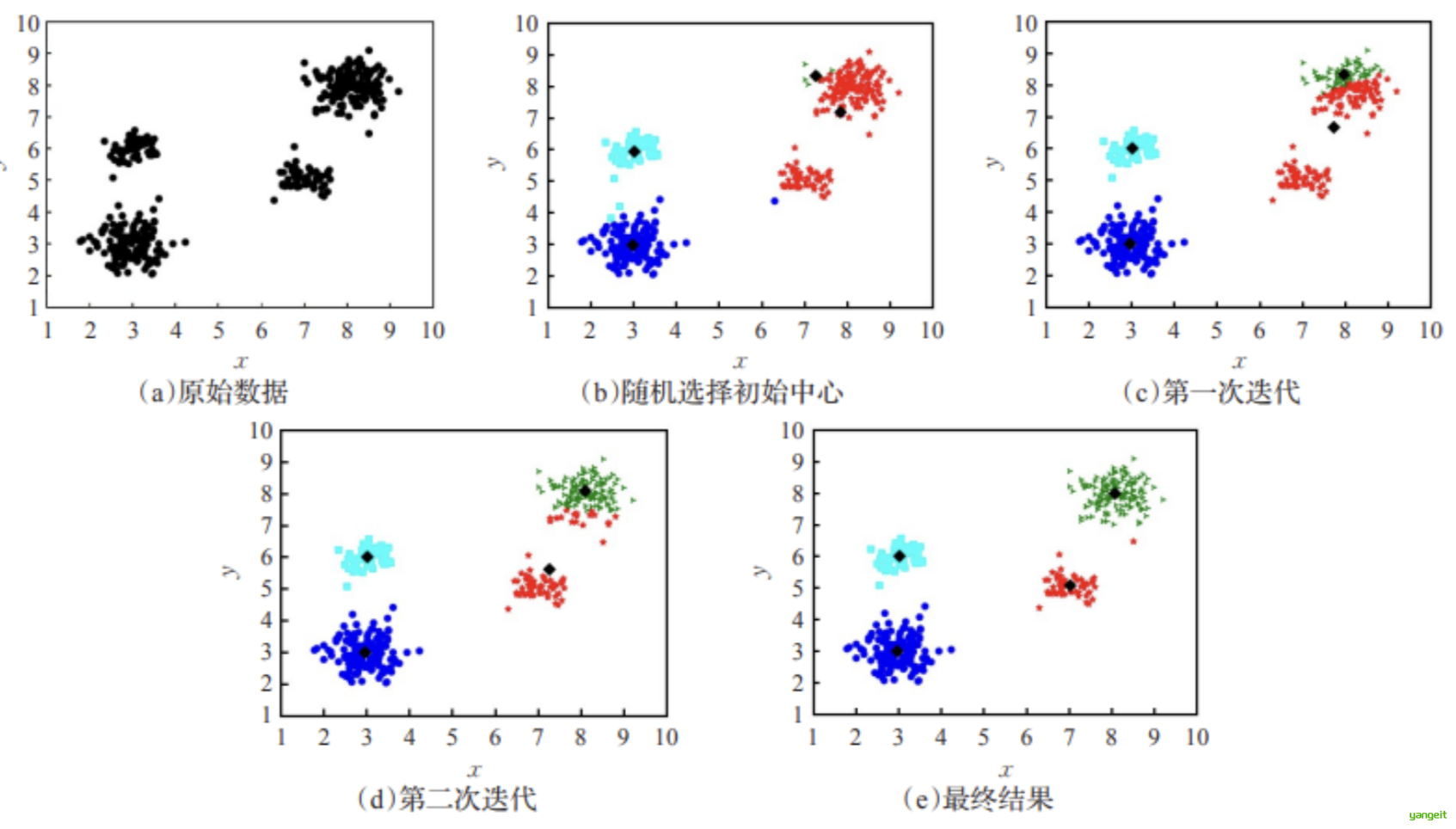

从上图容易看出，聚类结束之前，类中心会不断移动，而随着类中心的移动，样本的划分情况也会持续发生改变。

需求：年龄分组（K=3）
原始数据： [25, 30, 35, 40, 45, 50, 55, 60, 65, 70]

K-Means 聚类结果（假设）：

• 组1: [25, 30, 35]（中心点 ≈ 30）
• 组2: [40, 45, 50, 55]（中心点 ≈ 47.5）
• 组3: [60, 65, 70]（中心点 ≈ 65）

import pandas as pd
from sklearn.cluster import KMeans
# 原始数据
data = pd.DataFrame({"年龄": [25, 30, 35, 40, 45, 50, 55, 60, 65, 70]})
# 聚类分箱
kmeans = KMeans(n_clusters=3)# 定义聚类算法，n_clusters表示聚类中心数量
kmeans.fit(data) # 使用聚类算法进行聚类
data["年龄分组"] = kmeans.labels_  # 将聚类结果存储到DataFrame中
print(data)
# 每个类别的中心点
print(kmeans.cluster_centers_)

运行结果：

   年龄  年龄分组
0  25     2
1  30     2
2  35     2
3  40     0
4  45     0
5  50     0
6  55     0
7  60     1
8  65     1
9  70     1
# 中心点
[[47.5]
 [65. ]
 [30. ]]

✅ 避免数据分布不均问题。
✅ 可以处理非线性关系。
❌ 需要选择合适的聚类算法和参数。

---

上述案例是通过pandas实现的，下面我们通过sklearn实现数据离散化，也非常方便。

1. K桶离散化 （使用KBinsDiscretizer类将特征离散到K个桶（bin）中）

案例6 ：年龄分组

import pandas as pd
from sklearn.preprocessing import KBinsDiscretizer

# 原始数据
data = pd.DataFrame({"年龄": [25, 30, 35, 40, 45, 50, 55, 60, 65, 70]})

# K桶离散化
k_bins = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='quantile') 
 # 定义离散化算法，n_bins表示分箱数量，encode表示编码方式，strategy表示分箱策略(quantile表示等频分箱,uniform表示等宽分箱,kmeans表示聚类分箱)

# 正确方式：只选择需要离散化的列，并确保输入是二维数组
data["年龄分组"] = k_bins.fit_transform(data[["年龄"]]).astype(int)

print(data)
print("\n分箱边界:", k_bins.bin_edges_)

运行结果：

 年龄  年龄分组
0  25     0
1  30     0
2  35     0
3  40     0
4  45     1
5  50     1
6  55     1
7  60     2
8  65     2
9  70     2

分箱边界: [array([25.  , 41.25, 57.5 , 70.  ])]

可以发现，结果和上面的pandas.qcut方法是一致的。

✏️ ✏️ ✏️ 修改上面的分箱策略，uniform表示等宽分箱,kmeans表示聚类分箱 观察结果

4. 特征二值化

特征二值化是一种将 连续数值特征 或 多类别特征 转换为 二元值（0或1） 的数据预处理技术，核心思想是：
“设定一个阈值，大于阈值的值变为1，小于等于阈值的值变为0。”

案例7: 考试成绩二值化

import pandas as pd
from sklearn.preprocessing import Binarizer
# 原始数据
data = [[45], [80], [90], [55], [70]]
binarizer = Binarizer(threshold=60) # 定义二值化算法，threshold表示阈值
binary_scores = binarizer.fit_transform(data)  # 使用二值化算法进行二值化
print(binary_scores)

运行结果：

[[0]
 [1]
 [1]
 [0]
 [1]]

二值化好处是可以将数据转换为0和1，或者true和false ，方便后续的机器学习算法处理。

总结

课堂作业

学习完上一节，完成下列问题：

1. 参考上述代码，在jyupyter notebook中完成上述案例
2. 数据离散化的意义是什么？主要有哪些离散化方法？